We define what it means for a first order equation to be separable, and we work out solutions to a few examples of separable equations.
Separable Equations
A first order differential equation is separable if it can be written as
where the left side is a product of and a function of and the right side is a function of . Rewriting a separable differential equation in this form is called separation of variables.To see how to solve (eq:2.2.1), let’s first assume that is a solution. Let and be antiderivatives of and ; that is,
Then, from the chain rule, Therefore (eq:2.2.1) is equivalent to Integrating both sides of this equation and combining the constants of integration yields Although we derived this equation on the assumption that is a solution of (eq:2.2.1), we can now view it differently: Any differentiable function that satisfies (eq:2.2.3) for some constant is a solution of (eq:2.2.1). To see this, we differentiate both sides of (eq:2.2.3), using the chain rule on the left, to obtain which is equivalent to because of (eq:2.2.2).In conclusion, to solve (eq:2.2.1) it suffices to find functions and that satisfy (eq:2.2.2). Then any differentiable function that satisfies (eq:2.2.3) is a solution of (eq:2.2.1).
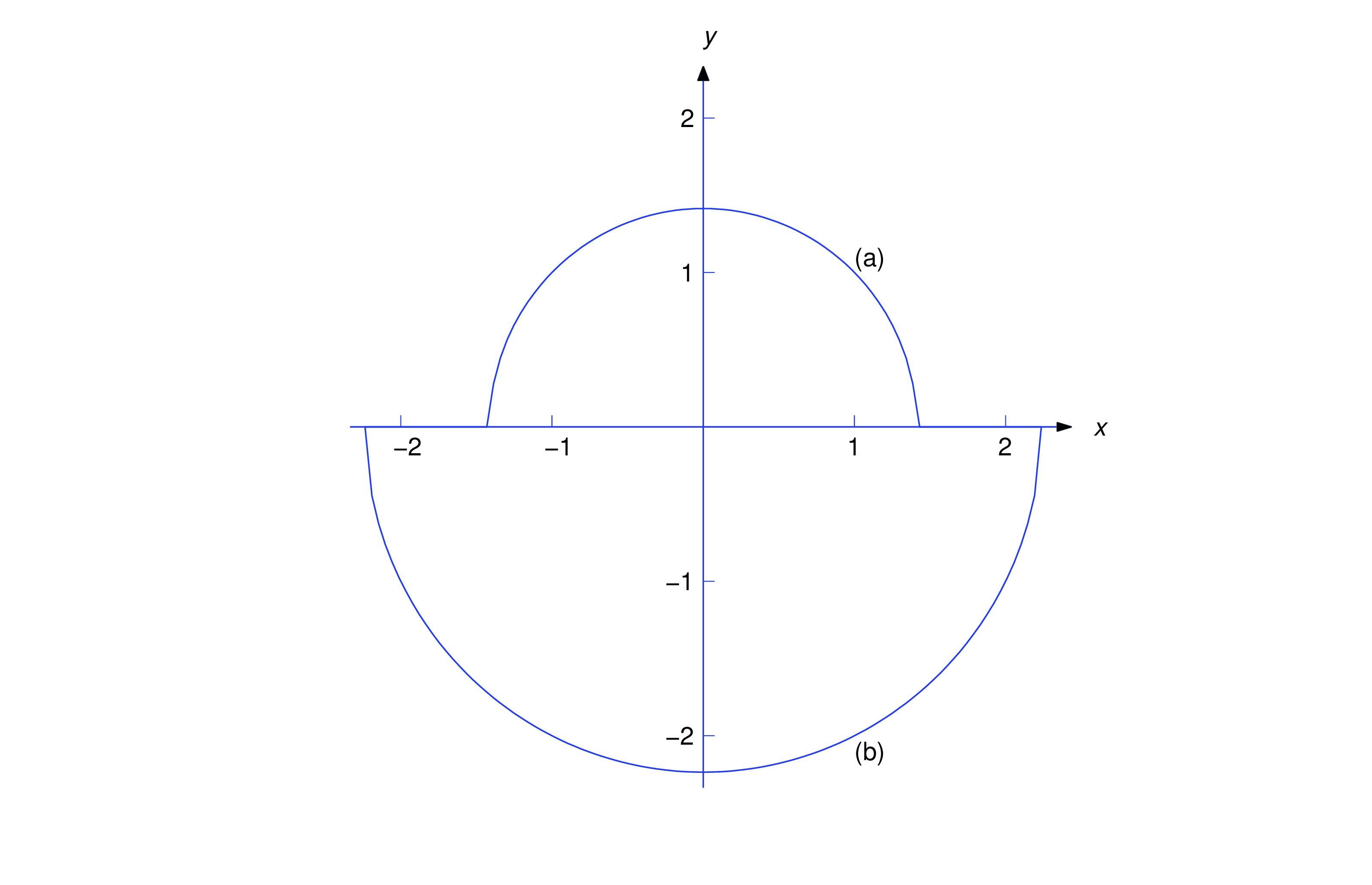
item:2.2.2b The solution of (eq:2.2.5) is positive when ; hence, it is of the form (eq:2.2.8). Substituting and into (eq:2.2.7) to satisfy the initial condition yields ; hence, the solution of (eq:2.2.5) is
item:2.2.2c The solution of (eq:2.2.6) is negative when and is therefore of the form (eq:2.2.9). Substituting and into (eq:2.2.7) to satisfy the initial condition yields . Hence, the solution of (eq:2.2.6) is
Implicit Solutions of Separable Equations
In Examples example:2.2.1 and example:2.2.2 we were able to solve the equation to obtain explicit formulas for solutions of the given separable differential equations. As we’ll see in the next example, this isn’t always possible. In this situation we must broaden our definition of a solution of a separable equation. The next theorem provides the basis for this modification. We omit the proof, which requires a result from advanced calculus called as the implicit function theorem.
It’s convenient to say that (eq:2.2.11) with arbitrary is an implicit solution of . Curves defined by (eq:2.2.11) are integral curves of . If satisfies (eq:2.2.10), we’ll say that (eq:2.2.11) is an implicit solution of the initial value problem (eq:2.2.12). However, keep these points in mind:
- For some choices of there may not be any differentiable functions that satisfy (eq:2.2.11).
- The function in (eq:2.2.11) (not (eq:2.2.11) itself) is a solution of .
item:2.2.3b Imposing the initial condition in (eq:2.2.15) yields , so . Therefore is an implicit solution of the initial value problem (eq:2.2.14). Although more than one differentiable function satisfies eq:2.2.13) near , it can be shown that there’s only one such function that satisfies the initial condition .
The figure below shows a direction field and some integral curves for (eq:2.2.13).
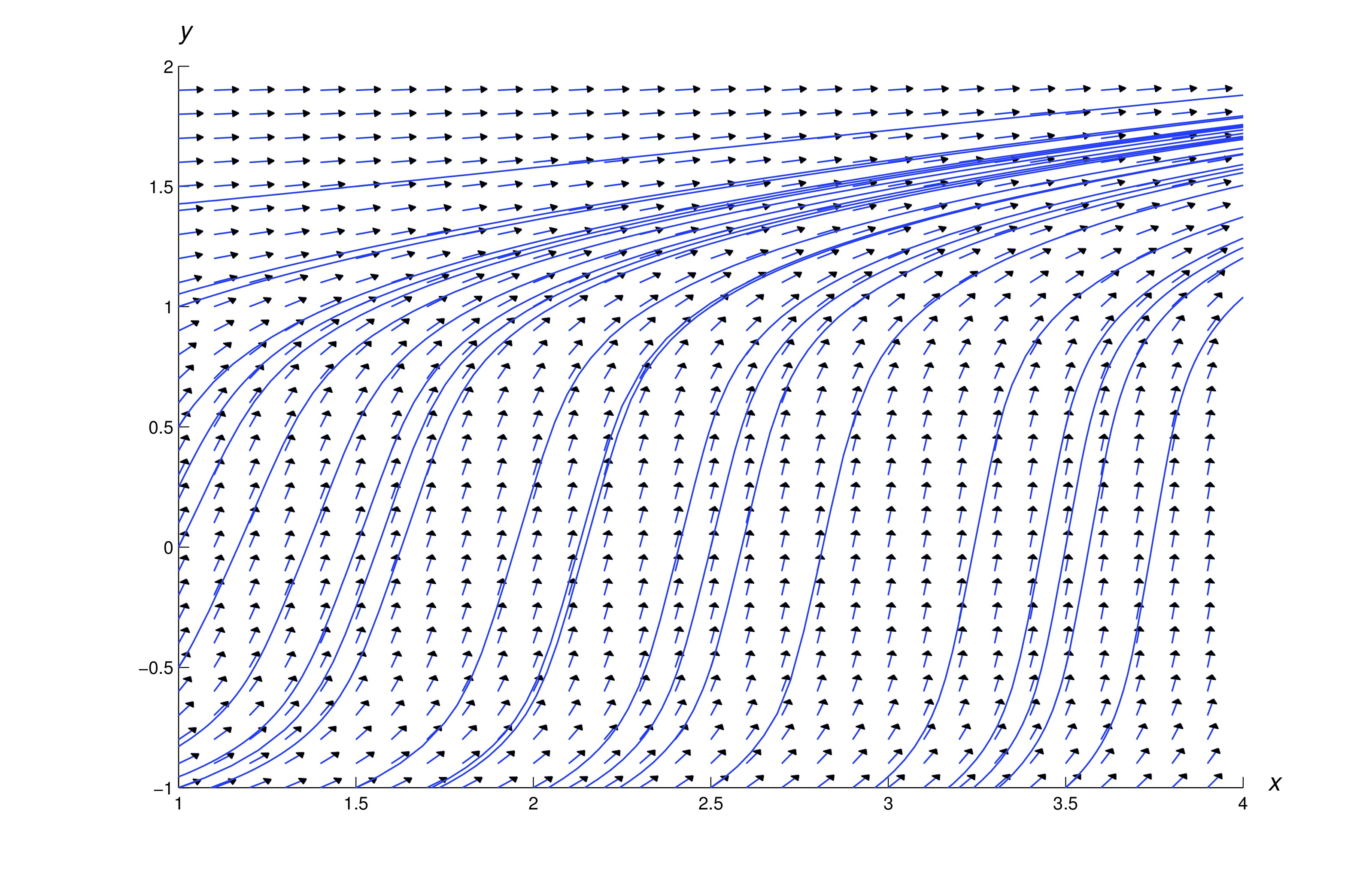
Constant Solutions of Separable Equations
An equation of the form is separable, since it can be rewritten as However, the division by is not legitimate if for some values of . The next two examples show how to deal with this problem.
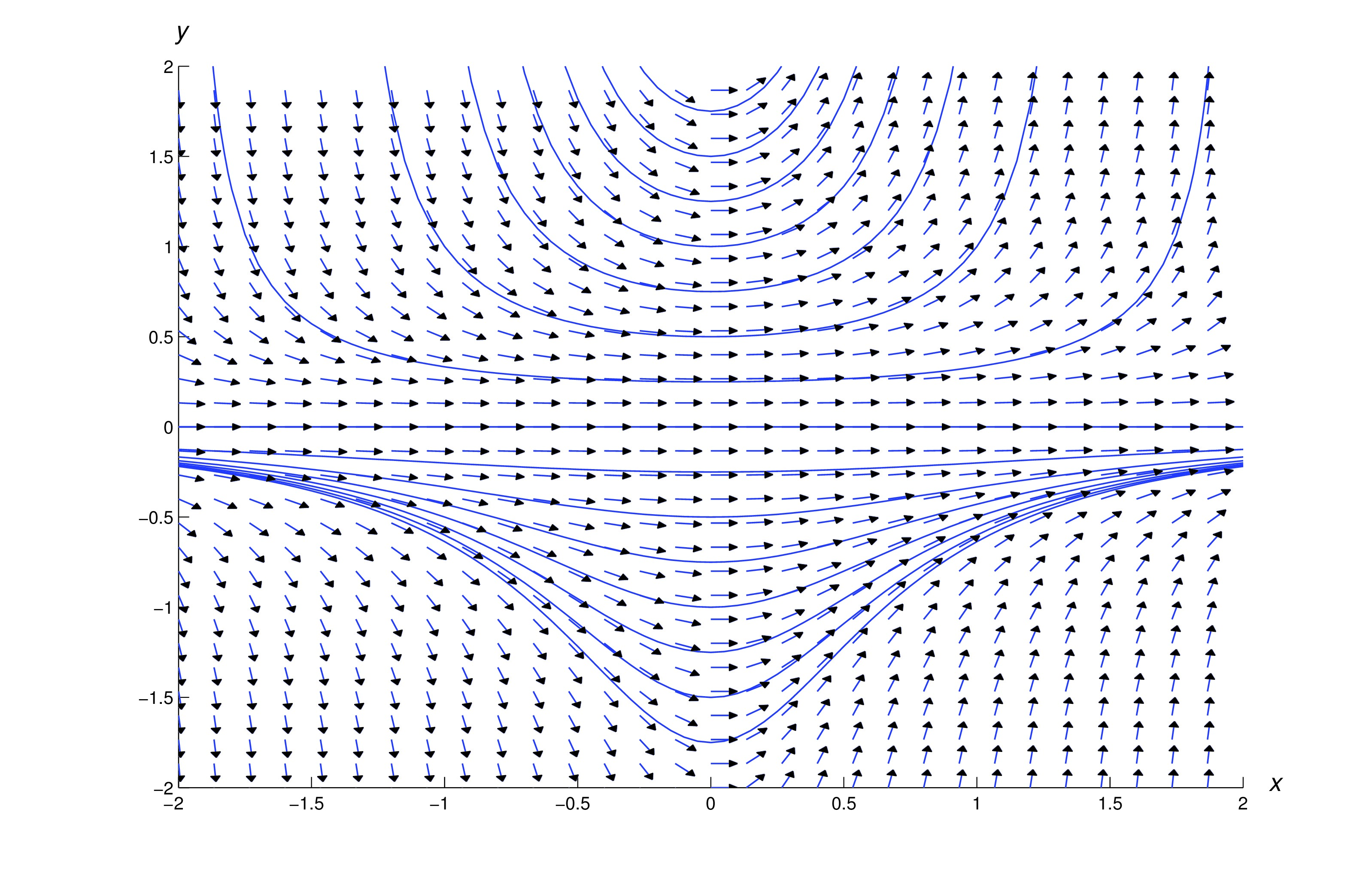
We’ve now shown that if is a solution of (eq:2.2.16) that is not identically zero, then must be of the form (eq:2.2.17). By substituting (eq:2.2.17) into (eq:2.2.16), you can verify that (eq:2.2.17) is a solution of (eq:2.2.16). Thus, solutions of (eq:2.2.16) are and the functions of the form (eq:2.2.17). Note that the solution isn’t of the form (eq:2.2.17) for any value of .
The figure below shows a direction field and some integral curves for (eq:2.2.16)
Here we must divide by to separate variables. This isn’t legitimate if is a solution of (eq:2.2.18) that equals for some value of . Two such solutions can be found by inspection: and . Now suppose is a solution of (eq:2.2.18) such that isn’t identically zero. Since is continuous there must be an interval on which is never zero. Since division by is legitimate for in this interval, we can separate variables in (eq:2.2.18) to obtain A partial fraction expansion on the left yields and integrating yields hence, Since for on the interval under discussion, the quantity can’t change sign in this interval. Therefore we can rewrite the last equation as where , depending upon the sign of on the interval. Solving for yields
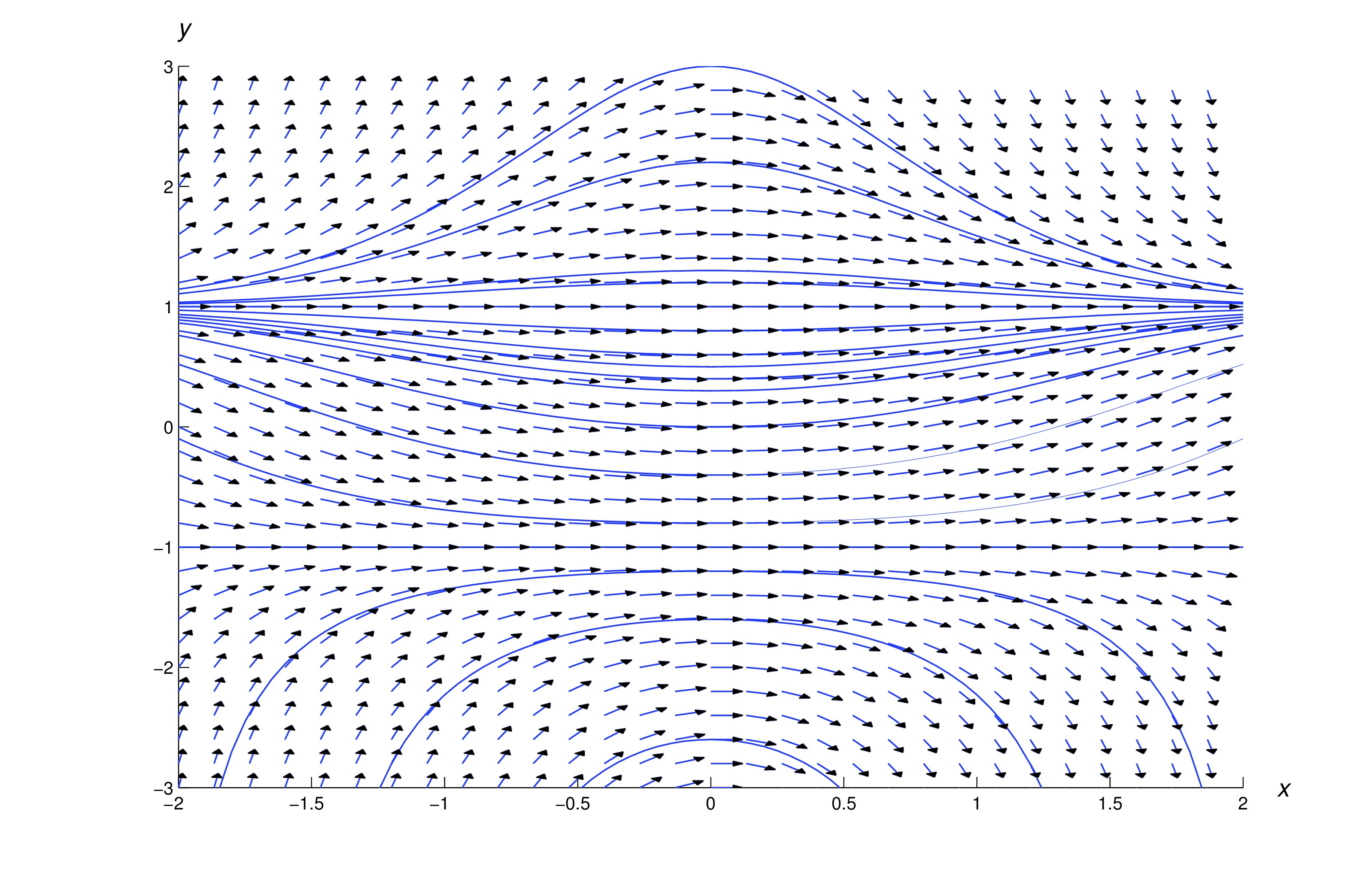
We’ve now shown that if is a solution of (eq:2.2.18) that is not identically equal to , then must be as in (eq:2.2.19). By substituting (eq:2.2.19) into (eq:2.2.18) you can verify that (eq:2.2.19) is a solution of (eq:2.2.18). Thus, the solutions of (eq:2.2.18) are , and the functions of the form (eq:2.2.19). Note that the constant solution can be obtained from this formula by taking ; however, the other constant solution, , can’t be obtained in this way.
The figure below shows a direction field and some integrals for (eq:2.2.18).
Text Source
Trench, William F., ”Elementary Differential Equations” (2013). Faculty Authored and Edited Books & CDs. 8. (CC-BY-NC-SA)