We study electric circuits as an application of second order linear differential equations.
The Circuit
In this section we consider the RLC circuit, shown schematically in the figure below.
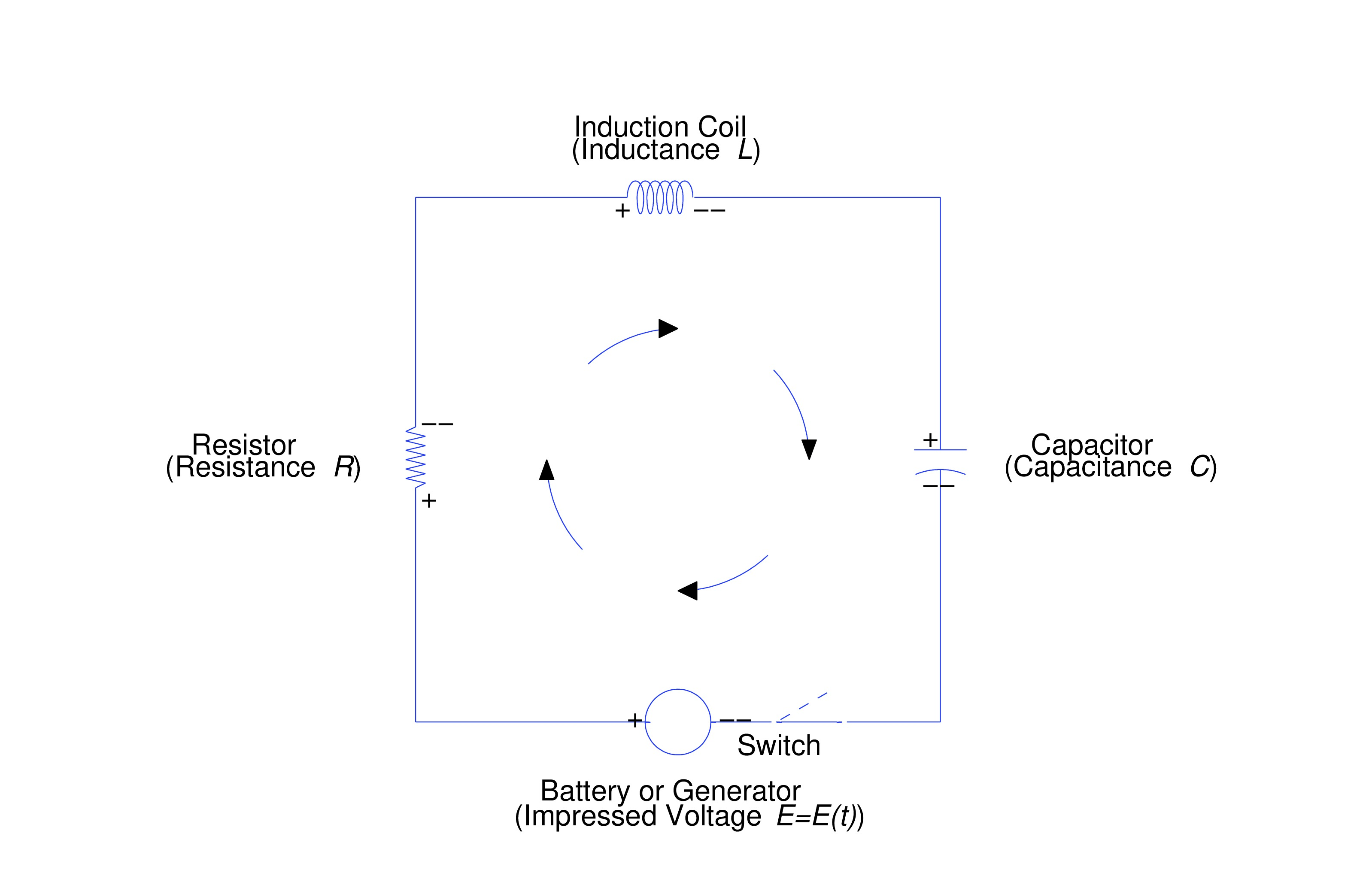
As we’ll see, the circuit is an electrical analog of a spring-mass system with damping.
Nothing happens while the switch is open (dashed line). When the switch is closed (solid line) we say that the circuit is closed. Differences in electrical potential in a closed circuit cause current to flow in the circuit. The battery or generator, shown in the figure, creates a difference in electrical potential between its two terminals, which we’ve marked arbitrarily as positive and negative. (We could just as well interchange the markings.) We’ll say that if the potential at the positive terminal is greater than the potential at the negative terminal, if the potential at the positive terminal is less than the potential at the negative terminal, and if the potential is the same at the two terminals. We call the impressed voltage.
At any time , the same current flows in all points of the circuit. We denote current by . We say that if the direction of flow is around the circuit from the positive terminal of the battery or generator back to the negative terminal, as indicated by the arrows in the figure, if the flow is in the opposite direction, and if no current flows at time .
Differences in potential occur at the resistor, induction coil, and capacitor. Note that the two sides of each of these components are also identified as positive and negative. The voltage drop across each component is defined to be the potential on the positive side of the component minus the potential on the negative side. This terminology is somewhat misleading, since “drop” suggests a decrease even though changes in potential are signed quantities and therefore may be increases. Nevertheless, we’ll go along with tradition and call them voltage drops. The voltage drop across the resistor, as shown in the figure, is given by
where is current and is a positive constant, the resistance of the resistor. The voltage drop across the induction coil is given by where is a positive constant, the inductance of the coil.A capacitor stores electrical charge , which is related to the current in the circuit by the equation
where is the charge on the capacitor at . The voltage drop across a capacitor is given by where is a positive constant, the capacitance of the capacitor.The following table names the units for the quantities that we’ve discussed. The units are defined so that
| Symbol | Name | Unit |
| Impressed Voltage | volt | |
| Current | ampere | |
| Charge | coulomb | |
| Resistance | ohm | |
| Inductance | henry | |
| Capacitance | farad | |
According to Kirchoff’s Law, the sum of the voltage drops in a closed circuit equals the impressed voltage. Therefore, from (eq:6.3.1), (eq:6.3.2), and (eq:6.3.4),
This equation contains two unknowns, the current in the circuit and the charge on the capacitor. However, (eq:6.3.3) implies that , so (eq:6.3.5) can be converted into the second order equation in . To find the current flowing in an circuit, we solve (eq:6.3.6) for and then differentiate the solution to obtain .In Trench 6.1 and 6.2 we encountered the equation
in connection with spring-mass systems. Except for notation this equation is the same as (eq:6.3.6). The correspondence between electrical and mechanical quantities connected with (eq:6.3.6) and (eq:6.3.7) is shown in the table below.
| Electrical | Mechanical | ||
| charge | displacement | ||
| curent | velocity | ||
| impressed voltage | external force | ||
| inductance | Mass | ||
| resistance | damping | ||
| 1/capacitance | spring constant | ||
The equivalence between (eq:6.3.6) and (eq:6.3.7) is an example of how mathematics unifies fundamental similarities in diverse physical phenomena. Since we’ve already studied the properties of solutions of (eq:6.3.7) in In Trench 6.1 and 6.2, we can obtain results concerning solutions of (eq:6.3.6) by simply changing notation, according to the table.
Free Oscillations
We say that an circuit is in free oscillation if for , so that (eq:6.3.6) becomes
The characteristic equation of (eq:6.3.8) is with roots There are three cases to consider, all analogous to the cases considered in In Trench 6.2 for free vibrations of a damped spring-mass system.Case 1. The oscillation is underdamped if . In this case, and in (eq:6.3.9) are complex conjugates, which we write as where The general solution of (eq:6.3.8) is which we can write as
where In the idealized case where , the solution (eq:6.3.10) reduces to which is analogous to the simple harmonic motion of an undamped spring-mass system in free vibration.Actual circuits are usually underdamped, so the case we’ve just considered is the most important. However, for completeness we’ll consider the other two possibilities.
Case 2. The oscillation is overdamped if . In this case, the zeros and of the characteristic polynomial are real, with (see (eq:6.3.9)), and the general solution of (eq:6.3.8) is
Case 3. The oscillation is critically damped if . In this case, and the general solution of (eq:6.3.8) is
If , the exponentials in (eq:6.3.10), (eq:6.3.11), and (eq:6.3.12) are negative, so the solution of any homogeneous initial value problem approaches zero exponentially as . Thus, all such solutions are transient, in the sense defined In Trench 6.2 in the discussion of forced vibrations of a spring-mass system with damping.
The characteristic equation of (eq:6.3.13) is which has complex zeros . Therefore the general solution of (eq:6.3.13) is
Differentiating this and collecting like terms yields To find the solution of the initial value problem (eq:6.3.14), we set in (eq:6.3.15) and (eq:6.3.16) to obtain therefore, and , so is the solution of (eq:6.3.14). Differentiating this yieldsForced Oscillations With Damping
An initial value problem for (eq:6.3.6) has the form
where is the initial charge on the capacitor and is the initial current in the circuit. We’ve already seen that if then all solutions of (eq:6.3.17) are transient. If , we know that the solution of (eq:6.3.17) has the form , where satisfies the complementary equation, and approaches zero exponentially as for any initial conditions , while depends only on and is independent of the initial conditions. As in the case of forced oscillations of a spring-mass system with damping, we call the steady state charge on the capacitor of the circuit. Since and also tends to zero exponentially as , we say that is the transient current and is the steady state current. In most applications we’re interested only in the steady state charge and current.
| Electrical | Mechanical | ||
| charge | displacement | ||
| curent | velocity | ||
| impressed voltage | external force | ||
| inductance | Mass | ||
| resistance | damping | ||
| 1/capacitance | spring constant | ||
yields the steady state charge where Therefore the steady state current in the circuit is
Text Source
Trench, William F., ”Elementary Differential Equations” (2013). Faculty Authored and Edited Books & CDs. 8. (CC-BY-NC-SA)