We study several applications of first order differential equations to elementary mechanics.
Newton’s Second Law of Motion
In this section we consider an object with constant mass moving along a line under a force . Let be the displacement of the object from a reference point on the line at time , and let and be the velocity and acceleration of the object at time . Thus, and , where the prime denotes differentiation with respect to . Newton’s second law of motion asserts that the force and the acceleration are related by the equation
Units
In applications there are three main sets of units in use for length, mass, force, and time: the cgs, mks, and British systems. All three use the second as the unit of time. Table 1 shows the other units. Consistent with (eq:4.3.1), the unit of force in each system is defined to be the force required to impart an acceleration of (one unit of length) to one unit of mass.
| Length | Force | Mass | |
| cgs | centimeter (cm) | dyne (d) | gram (g) |
| mks | meter (m) | newton (N) | kilogram (kg) |
| British | foot (ft) | pound (lb) | slug (sl) |
If we assume that Earth is a perfect sphere with constant mass density, Newton’s law of gravitation (discussed later in this section) asserts that the force exerted on an object by Earth’s gravitational field is proportional to the mass of the object and inversely proportional to the square of its distance from the center of Earth. However, if the object remains sufficiently close to Earth’s surface, we may assume that the gravitational force is constant and equal to its value at the surface. The magnitude of this force is , where is called the acceleration due to gravity. (To be completely accurate, should be called the magnitude of the acceleration due to gravity at Earth’s surface.) This quantity has been determined experimentally. Approximate values of are
In general, the force in (eq:4.3.1) may depend upon , , and . Since , (eq:4.3.1) can be written in the form
which is a second order equation. We’ll consider this equation with restrictions on later; however, since earlier we have dealt only with first order equations, we consider here only problems in which (eq:4.3.2) can be recast as a first order equation. This is possible if does not depend on , so (eq:4.3.2) is of the form Letting and yields a first order equation for : Solving this equation yields as a function of . If we know for some time , we can integrate to obtain as a function of .Equations of the form (eq:4.3.3) occur in problems involving motion through a resisting medium.
Motion Through a Resisting Medium Under Constant Gravitational Force
Now we consider an object moving vertically in some medium. We assume that the only forces acting on the object are gravity and resistance from the medium. We also assume that the motion takes place close to Earth’s surface and take the upward direction to be positive, so the gravitational force can be assumed to have the constant value . We’ll see that, under reasonable assumptions on the resisting force, the velocity approaches a limit as . We call this limit the terminal velocity.
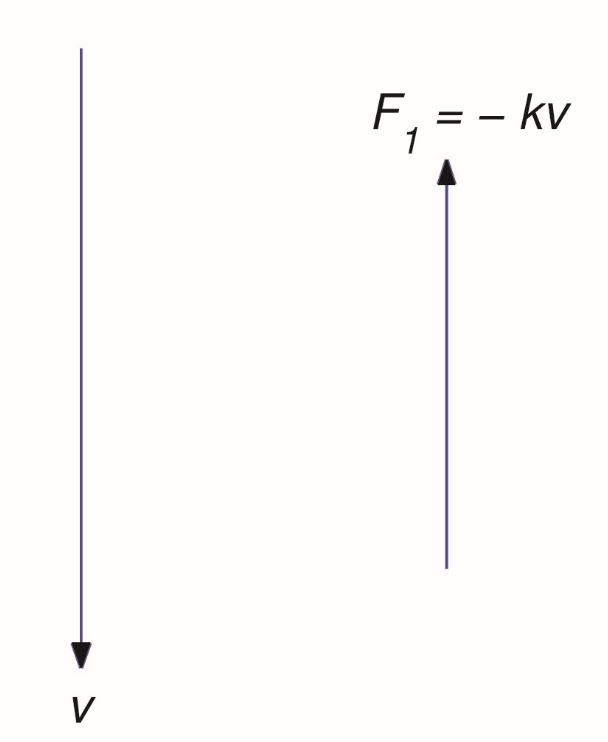
So On the other hand, if the object is moving upward (), the resisting force is downward, as shown.
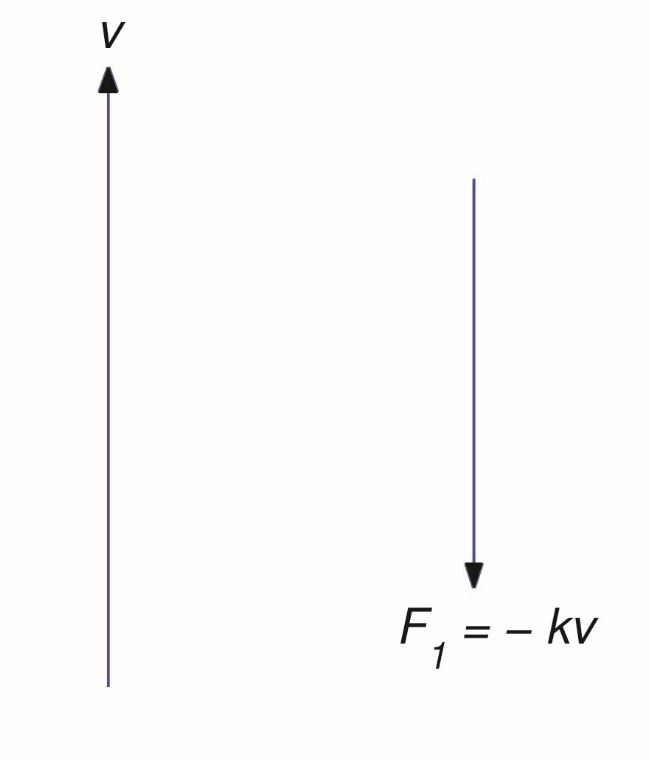
So Thus, (eq:4.3.4) can be written as
regardless of the sign of the velocity.From Newton’s second law of motion, so (eq:4.3.5) yields or
Since is a solution of the complementary equation, the solutions of (eq:4.3.6) are of the form , where , so . Hence, so Since , so and (eq:4.3.7) becomes Letting here shows that the terminal velocity is which is independent of the initial velocity (See figure below).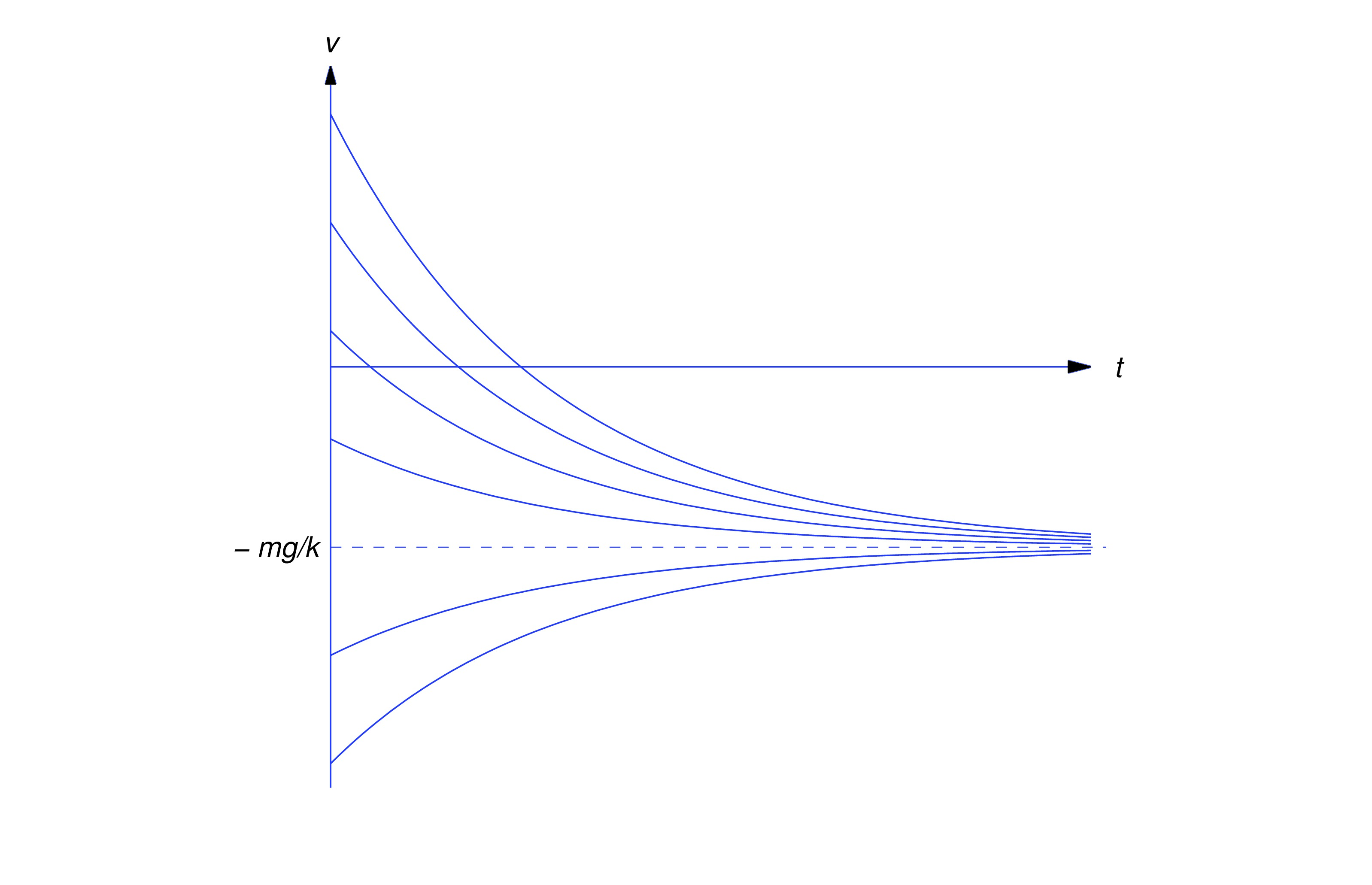
Separating variables yields and integrating this yields (Recall that is the number such that and .) Since , so is defined implicitly by
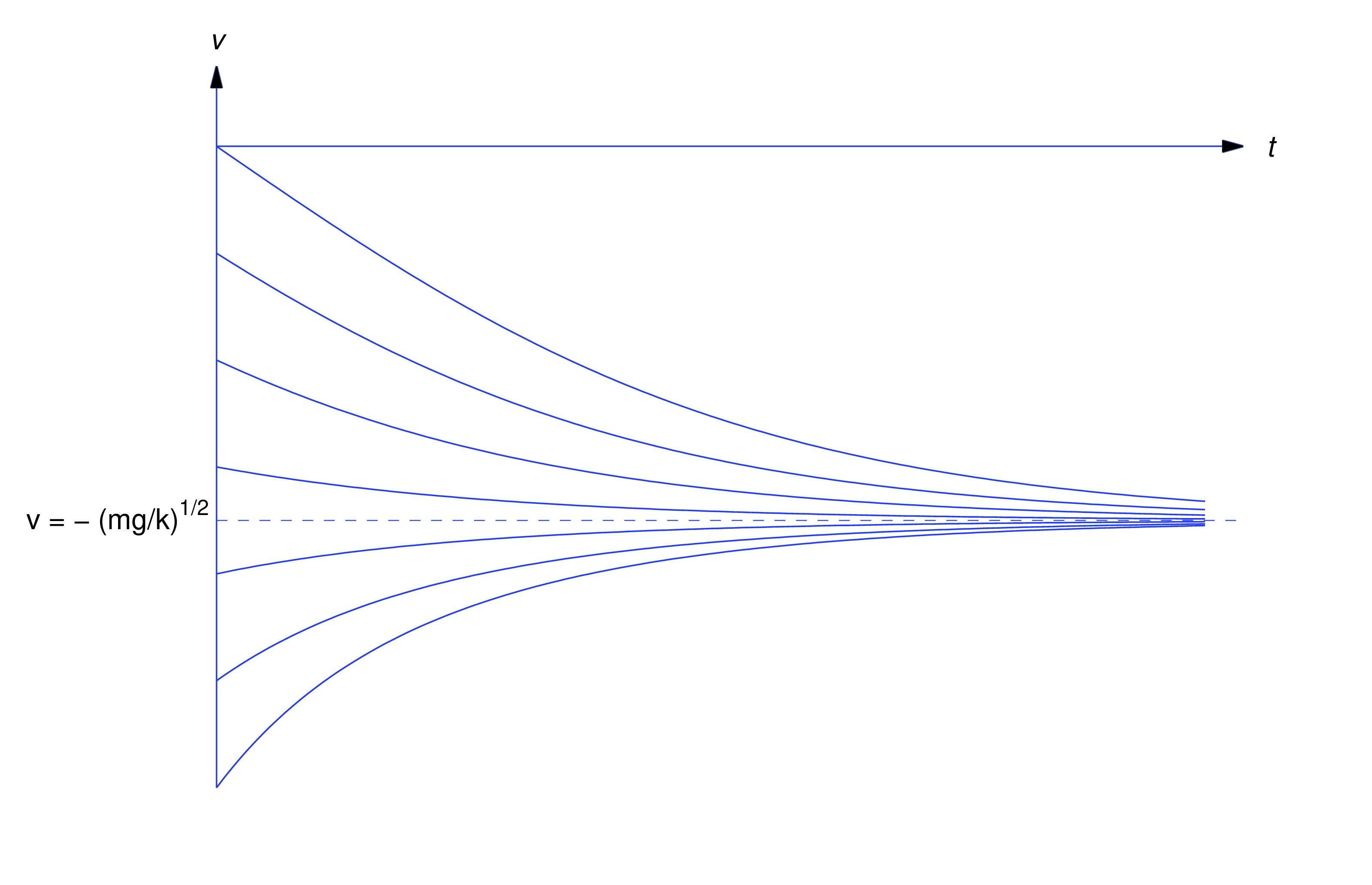
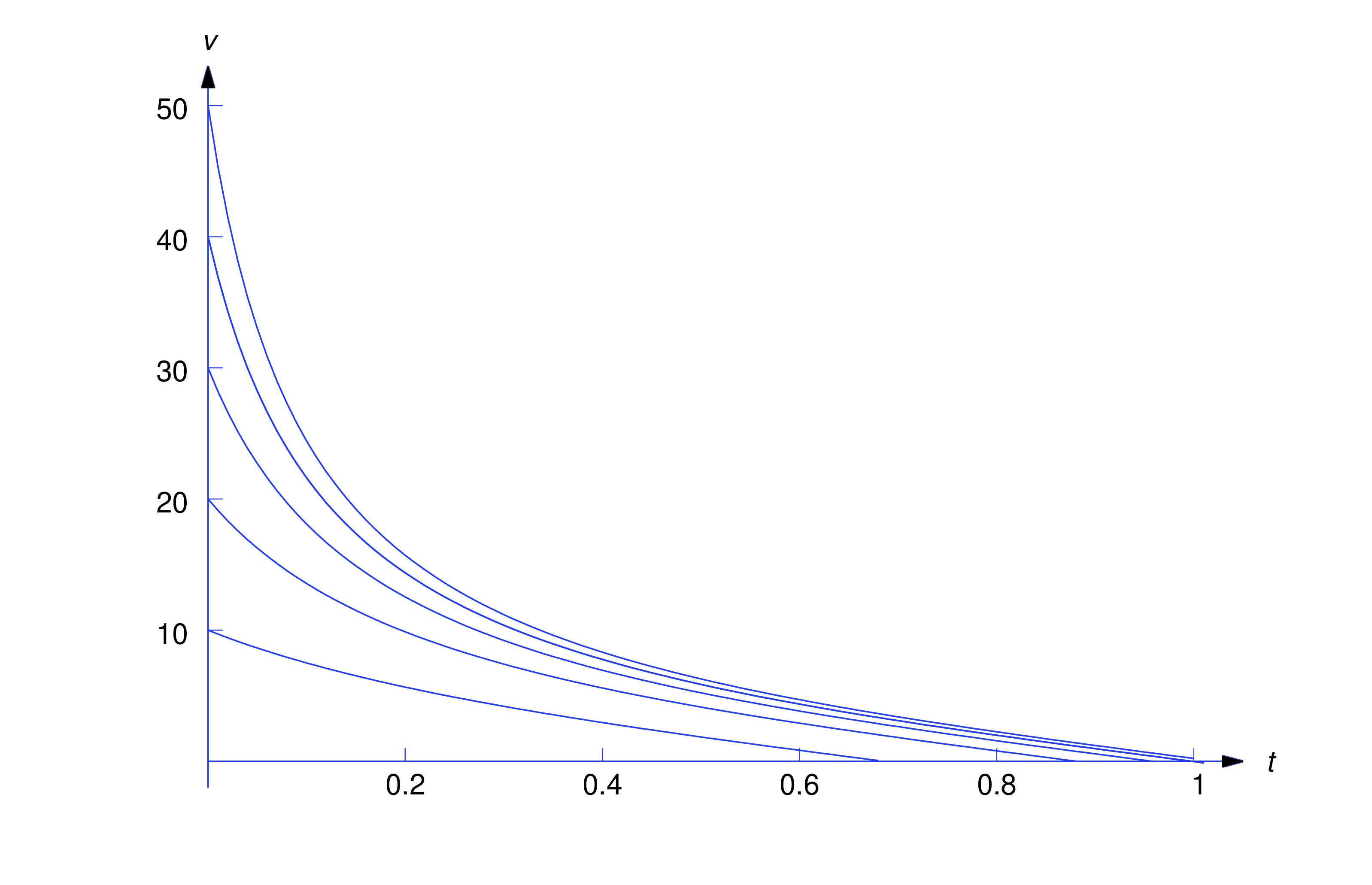
Solving this for yields Using the identity with and , and noting that , we can simplify (eq:4.3.17) toSince and , (eq:4.3.16) implies that Therefore Since for all , the time required for the mass to reach its maximum altitude is less than regardless of the initial velocity. The figure below shows graphs of over for various values of .
Escape Velocity
Suppose a space vehicle is launched vertically and its fuel is exhausted when the vehicle reaches an altitude above Earth, where is sufficiently large so that resistance due to Earth’s atmosphere can be neglected. Let be the time when burnout occurs. Assuming that the gravitational forces of all other celestial bodies can be neglected, the motion of the vehicle for is that of an object with constant mass under the influence of Earth’s gravitational force, which we now assume to vary inversely with the square of the distance from Earth’s center; thus, if we take the upward direction to be positive then gravitational force on the vehicle at an altitude above Earth is
where is Earth’s radius (see figure below).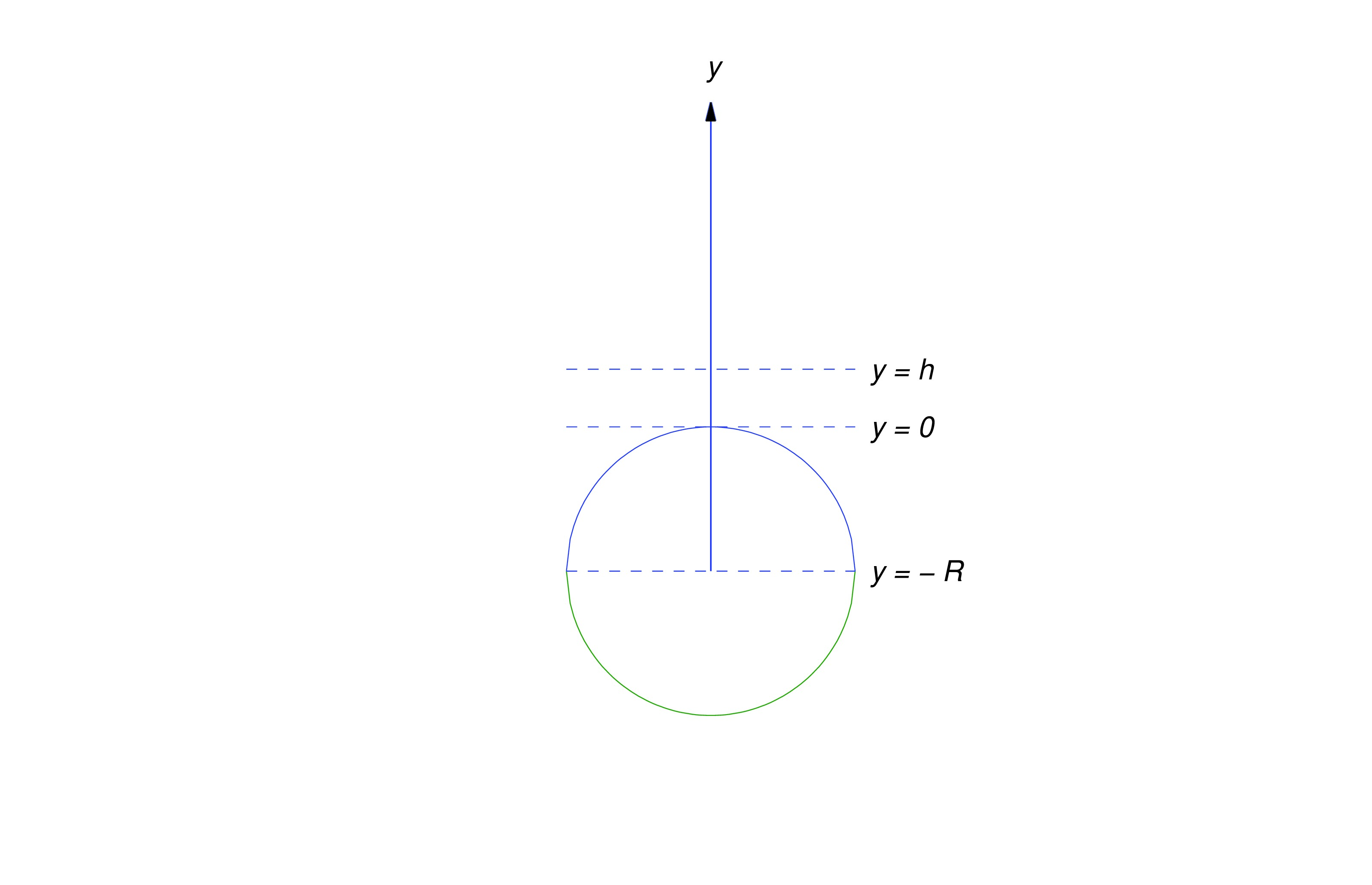
Since when , setting in (eq:4.3.18) yields therefore and (eq:4.3.18) can be written more specifically as
From Newton’s second law of motion, so (eq:4.3.19) implies that
We’ll show that there’s a number , called the escape velocity, with these properties:
- (a)
- If then for all , and the vehicle continues to climb for all ; that is, it “escapes” Earth. (Is it really so obvious that in this case?)
- (b)
- If then decreases to zero and becomes negative. Therefore the vehicle attains a maximum altitude and falls back to Earth.
Since (eq:4.3.20) is second order, we can’t solve it by methods discussed so far. However, we’re concerned with rather than , and is easier to find. Since the chain rule implies that Substituting this into (eq:4.3.20) yields the first order separable equation
When , the velocity is and the altitude is . Therefore we can obtain as a function of by solving the initial value problemIntegrating (eq:4.3.21) with respect to yields
Since , so (eq:4.3.22) becomes If the parenthetical expression in (eq:4.3.23) is nonnegative, so for . This proves that there’s an escape velocity . We’ll now prove that by showing that the vehicle falls back to Earth if If (eq:4.3.24) holds then the parenthetical expression in (eq:4.3.23) is negative and the vehicle will attain a maximum altitude that satisfies the equation The velocity will be zero at the maximum altitude, and the object will then fall to Earth under the influence of gravity.Text Source
Trench, William F., ”Elementary Differential Equations” (2013). Faculty Authored and Edited Books & CDs. 8. (CC-BY-NC-SA)