Mixing Problems

$\newenvironment {prompt}{}{} \newcommand {\DeclareMathOperator }[2]{\@OldDeclareMathOperator {##1}{##2}\immediate \write \myfile {\unexpanded {\DeclareMathOperator }{\unexpanded {##1}}{\unexpanded {##2}}}} \newcommand {\ungraded }[0]{} \newcommand {\inputGif }[1]{The gif ‘‘##1" would be inserted here when publishing online. } \newcommand {\npfourdigitsep }[0]{\nprt@numsepfourtrue } \newcommand {\npfourdigitnosep }[0]{\nprt@numsepfourfalse } \newcommand {\npaddmissingzero }[0]{\nprt@addmissingzerotrue } \newcommand {\npnoaddmissingzero }[0]{\nprt@addmissingzerofalse } \newcommand {\npaddplus }[0]{\nprt@addplus@mantissatrue } \newcommand {\npnoaddplus }[0]{\nprt@addplus@mantissafalse } \newcommand {\npaddplusexponent }[0]{\nprt@addplus@exponenttrue } \newcommand {\npnoaddplusexponent }[0]{\nprt@addplus@exponentfalse } \newcommand {\nprt@debug }[1]{} \newcommand {\npdecimalsign }[1]{\def \nprt@decimal {{##1}}} \newcommand {\npthousandsep }[1]{\def \nprt@separator@before {{##1}}\def \nprt@separator@after {{##1}}} \newcommand {\npthousandthpartsep }[1]{\def \nprt@separator@after {{##1}}} \newcommand {\npproductsign }[1]{\def \nprt@prod {\ensuremath {{}##1{}}}} \newcommand {\npunitseparator }[1]{\def \nprt@unitsep {{##1}}} \newcommand {\npdegreeseparator }[1]{\def \nprt@degreesep {{##1}}} \newcommand {\npcelsiusseparator }[1]{\def \nprt@celsiussep {{##1}}} \newcommand {\nppercentseparator }[1]{\def \nprt@percentsep {{##1}}} \newcommand {\nprounddigits }[1]{\def \nprt@rounddigits {##1}\def \nprt@roundnull {}\nprt@fillnull {\nprt@roundnull }{##1}} \newcommand {\npnoround }[0]{\nprounddigits {-1}} \newcommand {\nproundexpdigits }[1]{\def \nprt@roundexpdigits {##1}\def \nprt@roundexpnull {}\nprt@fillnull {\nprt@roundexpnull }{##1}} \newcommand {\npnoroundexp }[0]{\nproundexpdigits {-1}} \newcommand {\npnolpadding }[0]{\nplpadding [\@empty ]{-1}} \newcommand {\npreplacenull }[1]{\def \nprt@replacenull {##1}} \newcommand {\npprintnull }[0]{\let \nprt@replacenull =\@empty } \newcommand {\npunitcommand }[1]{\ensuremath {\mathrm {##1}}} \newcommand {\npdigits }[2]{\edef \nprt@mantissa@fixeddigits@before {##1}\edef \nprt@mantissa@fixeddigits@after {##2}\nprt@mantissa@fixeddigitstrue } \newcommand {\npnodigits }[0]{\nprt@mantissa@fixeddigitsfalse } \newcommand {\npnoexponentdigits }[0]{\nprt@exponent@fixeddigitsfalse } \newcommand {\nprt@error }[2]{\ifnprt@errormessage \PackageError {numprint}{##1}{##2}\else \PackageWarning {numprint}{##1}\fi \nprt@argumenterrortrue } \newcommand {\nprt@IfCharInString }[2]{\nprt@charfoundfalse \begingroup \def \nprt@searchfor {##1}\edef \nprt@argtwo {##2}\expandafter \nprt@@IfCharInString \nprt@argtwo \@empty \@empty \endgroup \ifnprt@charfound \expandafter \@firstoftwo \else \expandafter \@secondoftwo \fi } \newcommand {\nprt@plus@test }[0]{+} \newcommand {\nprt@minus@test }[0]{-} \newcommand {\nprt@plusminus@test }[0]{\pm } \newcommand {\nprt@numberlist }[0]{0123456789} \newcommand {\nprt@dotlist }[0]{.,} \newcommand {\nprt@explist }[0]{eEdD} \newcommand {\nprt@signlist }[0]{+-\pm } \newcommand {\nprt@ignorelist }[0]{} \newcommand {\nprt@testsign }[2]{\edef \nprt@commandname {##1}\edef \nprt@tmp {##2}\expandafter \nprt@@testsign \expandafter {\expandafter \nprt@commandname \expandafter }\nprt@tmp \@empty \@empty \@empty \@empty } \newcommand {\nprt@calcblockwidth }[3]{\edef \nprt@argone {##1}\edef \nprt@argtwo {##2}\edef \nprt@argthree {##3}\edef \nprt@mantissaname {mantissa}\edef \nprt@aftername {after}\ifx \nprt@argone \nprt@mantissaname \ifmmode \settowidth {\nprt@digitwidth }{$##30$}\settowidth {\nprt@sepwidth }{$##3\csname nprt@separator@##2\endcsname $}\settowidth {\nprt@decimalwidth }{$##3\nprt@decimal $}\else \settowidth {\nprt@digitwidth }{0}\settowidth {\nprt@sepwidth }{\csname nprt@separator@##2\endcsname }\settowidth {\nprt@decimalwidth }{\nprt@decimal }\fi \else \ifmmode \settowidth {\nprt@digitwidth }{$##3{}^{0}$}\settowidth {\nprt@sepwidth }{$##3{}^{\csname nprt@separator@##2\endcsname }$}\settowidth {\nprt@decimalwidth }{$##3{}^{\nprt@decimal }$}\else \settowidth {\nprt@digitwidth }{\textsuperscript {0}}\settowidth {\nprt@sepwidth }{\textsuperscript {\csname nprt@separator@##2\endcsname }}\settowidth {\nprt@decimalwidth }{\textsuperscript {\nprt@decimal }}\fi \fi \nprt@debug {Widths for ##1 ##2 decimal sign (\ifx \nprt@argthree \@empty text mode\else math mode ##3\fi ):\MessageBreak digits \the \nprt@digitwidth ,separators \the \nprt@sepwidth ,\MessageBreak decimal sign \the \nprt@decimalwidth }\ifnum \csname nprt@##1@fixeddigits@##2\endcsname <\csname thenprt@##1@digits##2\endcsname \PackageWarning {numprint}{##1 exceeds reserved space ##2\MessageBreak decimal sign}\fi \setlength {\nprt@blockwidth }{\csname nprt@##1@fixeddigits@##2\endcsname \nprt@digitwidth }\setcounter {nprt@blockcnt}{\csname nprt@##1@fixeddigits@##2\endcsname }\advance \c@nprt@blockcnt by -1\relax \divide \c@nprt@blockcnt 3\ifnprt@numsepfour \else \ifnum \csname nprt@##1@fixeddigits@before\endcsname <5 \ifnum \csname nprt@##1@fixeddigits@after\endcsname <5 \setcounter {nprt@blockcnt}{0}\fi \fi \fi \addtolength {\nprt@blockwidth }{\thenprt@blockcnt \nprt@sepwidth }\ifx \nprt@argtwo \nprt@aftername \expandafter \ifnum \csname nprt@##1@fixeddigits@after\endcsname >0 \addtolength {\nprt@blockwidth }{\the \nprt@decimalwidth }\fi \fi } \newcommand {\npunit }[1]{\def \nprt@unit {##1}} \newcommand {\npafternum }[1]{\def \nprt@afternum {##1}} \newcommand {\npmakebox }[0]{\@ifnextchar [{\nprt@makebox }{\makebox }} \newcommand {\nprt@makebox }[0]{} \newcommand {\nprt@round }[2]{\begingroup \edef \nprt@numname {##1}\ifnum ##2<0 \else \nprt@debug {\string \nprt@round : Round after ##2 digits for ##1}\setcounter {nprt@##1@digitsafter}{##2}\expandafter \g@addto@macro \csname nprt@##1@after\endcsname {\nprt@roundnull }\nprt@rndpos =##2 \nprt@roundupfalse \edef \nprt@tmpnum {\csname nprt@##1@after\endcsname }\edef \nprt@newnum {}\expandafter \nprt@round@after \nprt@tmpnum \@empty \@empty \expandafter \xdef \csname nprt@##1@after\endcsname {\nprt@newnum }\ifnprt@roundup \edef \nprt@tmpnum {\csname nprt@##1@before\endcsname }\edef \nprt@newnum {}\expandafter \nprt@round@before \nprt@tmpnum \@empty \@empty \ifnprt@roundup \expandafter \xdef \expandafter \nprt@newnum {1\nprt@newnum }\advance \csname c@nprt@##1@digitsbefore\endcsname by 1\relax \fi \expandafter \xdef \csname nprt@##1@before\endcsname {\nprt@newnum }\fi \fi \endgroup \ifnum ##2<0 \else \ifnum ##2=0 \csname nprt@##1@decimalfoundfalse\endcsname \else \csname nprt@##1@decimalfoundtrue\endcsname \fi \fi } \newcommand {\nprt@lpad }[3]{\ifnum ##2<0 \else \nprt@debug {\string \nprt@lpad : Padding ##1 with ##3 to a length of ##2}\ifnum \csname thenprt@##1@digitsbefore\endcsname <##2 \expandafter \xdef \csname nprt@##1@before\endcsname {##3\csname nprt@##1@before\endcsname }\advance \csname c@nprt@##1@digitsbefore\endcsname by 1\relax \nprt@lpad {##1}{##2}{##3}\fi \fi } \newcommand {\nprt@sign@+ }[0]{{\ensuremath {+}}} \newcommand {\nprt@sign@-}[0]{{\ensuremath {-}}} \newcommand {\nprt@sign@+-}[0]{{\ensuremath {\pm }}} \newcommand {\nprt@printsign }[2]{\nprt@debug {\string \nprt@printsign : ‘##2’}\edef \nprt@marg {##2}\csname ifnprt@addplus@##1\endcsname \ifx \nprt@marg \@empty \edef \nprt@marg {+}\fi \fi \ifx \nprt@marg \@empty \else \@ifundefined {nprt@sign@\nprt@marg }{\PackageWarning {numprint}{Unknown sign ‘\nprt@marg ’. Print as typed in}\nprt@marg }{\csname nprt@sign@\nprt@marg \endcsname }\fi } \newcommand {\nprt@printbefore }[1]{\ifnprt@addmissingzero \ifnum \csname thenprt@##1@digitsbefore\endcsname =0 \expandafter \edef \csname nprt@##1@before\endcsname {0}\advance \csname c@nprt@##1@digitsbefore\endcsname by 1\relax \fi \fi \begingroup \edef \nprt@numbertoprint {\csname nprt@##1@before\endcsname }\ifnprt@numsepfour \else \ifnum \csname thenprt@##1@digitsbefore\endcsname <5 \ifnum \csname thenprt@##1@digitsafter\endcsname <5 \nprt@shortnumbertrue \fi \fi \fi \ifnprt@shortnumber \nprt@numbertoprint \else \setcounter {nprt@blockcnt}{\csname thenprt@##1@digitsbefore\endcsname }\advance \c@nprt@blockcnt by -1\relax \divide \c@nprt@blockcnt 3\setcounter {nprt@digitsfirstblock}{\csname thenprt@##1@digitsbefore\endcsname }\setcounter {nprt@cntprint}{\thenprt@blockcnt }\multiply \c@nprt@cntprint 3\advance \c@nprt@digitsfirstblock by -\thenprt@cntprint \relax \ifnum \thenprt@digitsfirstblock =1 \expandafter \nprt@printone \nprt@numbertoprint \@empty \else \ifnum \thenprt@digitsfirstblock =2 \expandafter \nprt@printtwo \nprt@numbertoprint \@empty \else \ifnum \thenprt@digitsfirstblock =3 \expandafter \nprt@printthree \nprt@numbertoprint \@empty \else \ifnum \thenprt@digitsfirstblock =0 \else \PackageError {numprint}{internal error}{}\fi \fi \fi \fi \fi \endgroup } \newcommand {\nprt@printafter }[1]{\csname ifnprt@##1@decimalfound\endcsname \ifnprt@addmissingzero \ifnum \csname thenprt@##1@digitsafter\endcsname =0 \expandafter \edef \csname nprt@##1@after\endcsname {0}\advance \csname c@nprt@##1@digitsafter\endcsname by 1\relax \fi \fi \ifx \nprt@replacenull \@empty \else \ifnum \csname thenprt@##1@digitsafter\endcsname =0 \expandafter \edef \csname nprt@##1@after\endcsname {0}\advance \csname c@nprt@##1@digitsafter\endcsname by 1\relax \fi \fi \fi \begingroup \edef \nprt@numbertoprint {\csname nprt@##1@after\endcsname }\ifx \nprt@numbertoprint \@empty \else \ifnprt@numsepfour \else \ifnum \csname thenprt@##1@digitsbefore\endcsname <5 \ifnum \csname thenprt@##1@digitsafter\endcsname <5 \nprt@shortnumbertrue \fi \fi \fi \ifx \nprt@replacenull \@empty \else \ifnum \nprt@numbertoprint =0 \nprt@shortnumbertrue \edef \nprt@numbertoprint {\nprt@replacenull }\fi \fi \ifnprt@shortnumber \nprt@numbertoprint \else \expandafter \nprt@printthree@after \nprt@numbertoprint \@empty \@empty \@empty \fi \fi \endgroup } \newcommand {\npdefunit }[3]{\if ##3* \else \expandafter \def \csname nprt@factor@##1\endcsname {##3}\fi \expandafter \def \csname nprt@unit@##1\endcsname {##2}} \newcommand {\nprt@ifundefined }[1]{\begingroup \expandafter \expandafter \expandafter \endgroup \expandafter \ifx \csname ##1\endcsname \relax \expandafter \@firstoftwo \else \expandafter \@secondoftwo \fi } \newcommand {\nprt@addto }[2]{\expandafter \nprt@ifundefined {##1}{}{\expandafter \addto \expandafter {\csname ##1\endcsname }{##2}}} \newcommand {\npaddtolanguage }[2]{\nprt@addto {extras##1}{\csname npstyle##2\endcsname }\nprt@addto {noextras##1}{\npstyledefault }} \newcommand {\npstyledefault }[0]{\npthousandsep {\,}\npdecimalsign {,}\npproductsign {\cdot }\npunitseparator {\,}\npdegreeseparator {}\npcelsiusseparator {\nprt@unitsep }\nppercentseparator {\nprt@unitsep }} \newcommand {\npstylegerman }[0]{\npthousandsep {\,}\npdecimalsign {,}\npproductsign {\cdot }\npunitseparator {\,}\npdegreeseparator {}\npcelsiusseparator {\nprt@unitsep }\nppercentseparator {\nprt@unitsep }} \newcommand {\npstyleenglish }[0]{\npthousandsep {,}\npdecimalsign {.}\npproductsign {\times }\npunitseparator {\,}\npdegreeseparator {}\npcelsiusseparator {\nprt@unitsep }\nppercentseparator {\nprt@unitsep }} \newcommand {\npstyleportuguese }[0]{\npthousandsep {.}\npdecimalsign {,}\npproductsign {\cdot }\npunitseparator {\,}\npdegreeseparator {}\npcelsiusseparator {\nprt@unitsep }\nppercentseparator {\nprt@unitsep }} \newcommand {\npstyledutch }[0]{\npthousandsep {\,}\npdecimalsign {,}\npproductsign {\cdot }\npunitseparator {\,}\npdegreeseparator {}\npcelsiusseparator {\nprt@unitsep }\nppercentseparator {}} \newcommand {\npstylefrench }[0]{\npthousandsep {~}\npdecimalsign {,}\npproductsign {\cdot }\npunitseparator {\,}\npdegreeseparator {}\npcelsiusseparator {\nprt@unitsep }\nppercentseparator {\nprt@unitsep }} \newcommand {\nprt@renameerror }[1]{\expandafter \def \csname ##1\endcsname {\PackageError {numprint}{This command has been renamed to\MessageBreak \string \np ##1}{In order to avoid problems with other packages and for consistency,this\MessageBreak command has been renamed in this version.}}} \newcommand {\tkz@getdecimal }[1]{\expandafter \@getdecimal ##1.\@nil } \newcommand {\CountToken }[1]{\c@pgfmath@countb 0 \expandafter \C@untToken ##1\@nil } \newcommand {\C@untToken }[0]{\afterassignment \C@untT@ken \let \CurrT@ken = } \newcommand {\C@untT@ken }[0]{\ifx \CurrT@ken \@nil \else \advance \c@pgfmath@countb by1 \expandafter \C@untToken \fi } \newcommand {\tdplotsinandcos }[3]{\pgfmathsetmacro {##1}{sin(##3)}\pgfmathsetmacro {##2}{cos(##3)}} \newcommand {\tdplotmult }[3]{\pgfmathsetmacro {##1}{##2*##3}} \newcommand {\tdplotdiv }[3]{\pgfmathsetmacro {##1}{##2/##3}} \newcommand {\tdplotcheckdiff }[5]{\par \par \pgfmathparse { abs(##2 -##1)<##3 } \par \ifthenelse {\equal {\pgfmathresult }{1}}{##4}{##5} } \newcommand {\tdplotsetmaincoords }[2]{\pgfmathsetmacro {\tdplotmaintheta }{##1} \pgfmathsetmacro {\tdplotmainphi }{##2} \tdplotcalctransformmainscreen \tikzset {tdplot_main_coords/.style={x={(\raarot cm,\rbarot cm)},y={(\rabrot cm,\rbbrot cm)},z={(\racrot cm,\rbcrot cm)}}}} \newcommand {\tdplotcalctransformmainscreen }[0]{\tdplotsinandcos {\sintheta }{\costheta }{\tdplotmaintheta }\tdplotsinandcos {\sinphi }{\cosphi }{\tdplotmainphi }\tdplotmult {\stsp }{\sintheta }{\sinphi }\tdplotmult {\stcp }{\sintheta }{\cosphi }\tdplotmult {\ctsp }{\costheta }{\sinphi }\tdplotmult {\ctcp }{\costheta }{\cosphi }\pgfmathsetmacro {\raarot }{\cosphi }\pgfmathsetmacro {\rabrot }{\sinphi }\pgfmathsetmacro {\racrot }{0}\pgfmathsetmacro {\rbarot }{-\ctsp }\pgfmathsetmacro {\rbbrot }{\ctcp }\pgfmathsetmacro {\rbcrot }{\sintheta }\pgfmathsetmacro {\rcarot }{\stsp }\pgfmathsetmacro {\rcbrot }{-\stcp }\pgfmathsetmacro {\rccrot }{\costheta }} \newcommand {\tdplotcalctransformrotmain }[0]{\tdplotsinandcos {\sinalpha }{\cosalpha }{\tdplotalpha } \tdplotsinandcos {\sinbeta }{\cosbeta }{\tdplotbeta } \tdplotsinandcos {\singamma }{\cosgamma }{\tdplotgamma } \tdplotmult {\sasb }{\sinalpha }{\sinbeta } \tdplotmult {\sbsg }{\sinbeta }{\singamma } \tdplotmult {\sasg }{\sinalpha }{\singamma } \tdplotmult {\sasbsg }{\sasb }{\singamma } \tdplotmult {\sacb }{\sinalpha }{\cosbeta } \tdplotmult {\sacg }{\sinalpha }{\cosgamma } \tdplotmult {\sbcg }{\sinbeta }{\cosgamma } \tdplotmult {\sacbsg }{\sacb }{\singamma } \tdplotmult {\sacbcg }{\sacb }{\cosgamma } \tdplotmult {\casb }{\cosalpha }{\sinbeta } \tdplotmult {\cacb }{\cosalpha }{\cosbeta } \tdplotmult {\cacg }{\cosalpha }{\cosgamma } \tdplotmult {\casg }{\cosalpha }{\singamma } \tdplotmult {\cacbsg }{\cacb }{\singamma } \tdplotmult {\cacbcg }{\cacb }{\cosgamma } \pgfmathsetmacro {\raaeul }{\cacbcg -\sasg } \pgfmathsetmacro {\rabeul }{-\cacbsg -\sacg } \pgfmathsetmacro {\raceul }{\casb } \pgfmathsetmacro {\rbaeul }{\sacbcg + \casg } \pgfmathsetmacro {\rbbeul }{-\sacbsg + \cacg } \pgfmathsetmacro {\rbceul }{\sasb } \pgfmathsetmacro {\rcaeul }{-\sbcg } \pgfmathsetmacro {\rcbeul }{\sbsg } \pgfmathsetmacro {\rcceul }{\cosbeta } } \newcommand {\tdplotcalctransformmainrot }[0]{\tdplotsinandcos {\sinalpha }{\cosalpha }{\tdplotalpha } \tdplotsinandcos {\sinbeta }{\cosbeta }{\tdplotbeta } \tdplotsinandcos {\singamma }{\cosgamma }{\tdplotgamma } \tdplotmult {\sasb }{\sinalpha }{\sinbeta } \tdplotmult {\sbsg }{\sinbeta }{\singamma } \tdplotmult {\sasg }{\sinalpha }{\singamma } \tdplotmult {\sasbsg }{\sasb }{\singamma } \tdplotmult {\sacb }{\sinalpha }{\cosbeta } \tdplotmult {\sacg }{\sinalpha }{\cosgamma } \tdplotmult {\sbcg }{\sinbeta }{\cosgamma } \tdplotmult {\sacbsg }{\sacb }{\singamma } \tdplotmult {\sacbcg }{\sacb }{\cosgamma } \tdplotmult {\casb }{\cosalpha }{\sinbeta } \tdplotmult {\cacb }{\cosalpha }{\cosbeta } \tdplotmult {\cacg }{\cosalpha }{\cosgamma } \tdplotmult {\casg }{\cosalpha }{\singamma } \tdplotmult {\cacbsg }{\cacb }{\singamma } \tdplotmult {\cacbcg }{\cacb }{\cosgamma } \pgfmathsetmacro {\raaeul }{\cacbcg -\sasg } \pgfmathsetmacro {\rabeul }{\sacbcg + \casg } \pgfmathsetmacro {\raceul }{-\sbcg } \pgfmathsetmacro {\rbaeul }{-\cacbsg -\sacg } \pgfmathsetmacro {\rbbeul }{-\sacbsg + \cacg } \pgfmathsetmacro {\rbceul }{\sbsg } \pgfmathsetmacro {\rcaeul }{\casb } \pgfmathsetmacro {\rcbeul }{\sasb } \pgfmathsetmacro {\rcceul }{\cosbeta } } \newcommand {\tdplottransformmainrot }[3]{\tdplotcalctransformmainrot \par \pgfmathsetmacro {\tdplotresx }{\raaeul * ##1 + \rabeul * ##2 + \raceul * ##3} \pgfmathsetmacro {\tdplotresy }{\rbaeul * ##1 + \rbbeul * ##2 + \rbceul * ##3} \pgfmathsetmacro {\tdplotresz }{\rcaeul * ##1 + \rcbeul * ##2 + \rcceul * ##3} } \newcommand {\tdplottransformrotmain }[3]{\tdplotcalctransformrotmain \par \pgfmathsetmacro {\tdplotresx }{\raaeul * ##1 + \rabeul * ##2 + \raceul * ##3} \pgfmathsetmacro {\tdplotresy }{\rbaeul * ##1 + \rbbeul * ##2 + \rbceul * ##3} \pgfmathsetmacro {\tdplotresz }{\rcaeul * ##1 + \rcbeul * ##2 + \rcceul * ##3} } \newcommand {\tdplottransformmainscreen }[3]{\tdplotcalctransformmainscreen \par \pgfmathsetmacro {\tdplotresx }{\raarot * ##1 + \rabrot * ##2 + \racrot * ##3} \pgfmathsetmacro {\tdplotresy }{\rbarot * ##1 + \rbbrot * ##2 + \rbcrot * ##3} } \newcommand {\tdplotsetrotatedcoords }[3]{\pgfmathsetmacro {\tdplotalpha }{##1} \pgfmathsetmacro {\tdplotbeta }{##2} \pgfmathsetmacro {\tdplotgamma }{##3} \tdplotcalctransformrotmain \par \tdplotmult {\raaeaa }{\raarot }{\raaeul } \tdplotmult {\rabeba }{\rabrot }{\rbaeul } \tdplotmult {\raceca }{\racrot }{\rcaeul } \tdplotmult {\raaeab }{\raarot }{\rabeul } \tdplotmult {\rabebb }{\rabrot }{\rbbeul } \tdplotmult {\racecb }{\racrot }{\rcbeul } \tdplotmult {\raaeac }{\raarot }{\raceul } \tdplotmult {\rabebc }{\rabrot }{\rbceul } \tdplotmult {\racecc }{\racrot }{\rcceul } \tdplotmult {\rbaeaa }{\rbarot }{\raaeul } \tdplotmult {\rbbeba }{\rbbrot }{\rbaeul } \tdplotmult {\rbceca }{\rbcrot }{\rcaeul } \tdplotmult {\rbaeab }{\rbarot }{\rabeul } \tdplotmult {\rbbebb }{\rbbrot }{\rbbeul } \tdplotmult {\rbcecb }{\rbcrot }{\rcbeul } \tdplotmult {\rbaeac }{\rbarot }{\raceul } \tdplotmult {\rbbebc }{\rbbrot }{\rbceul } \tdplotmult {\rbcecc }{\rbcrot }{\rcceul } \pgfmathsetmacro {\raarc }{\raaeaa + \rabeba + \raceca } \pgfmathsetmacro {\rabrc }{\raaeab + \rabebb + \racecb } \pgfmathsetmacro {\racrc }{\raaeac + \rabebc + \racecc } \pgfmathsetmacro {\rbarc }{\rbaeaa + \rbbeba + \rbceca } \pgfmathsetmacro {\rbbrc }{\rbaeab + \rbbebb + \rbcecb } \pgfmathsetmacro {\rbcrc }{\rbaeac + \rbbebc + \rbcecc } \tikzset {tdplot_rotated_coords/.append style={x={(\raarc cm,\rbarc cm)},y={(\rabrc cm,\rbbrc cm)},z={(\racrc cm,\rbcrc cm)}}}} \newcommand {\tdplotsetrotatedcoordsorigin }[1]{\tikzset {tdplot_rotated_coords/.append style={shift=##1}}} \newcommand {\tdplotresetrotatedcoordsorigin }[0]{\tikzset {tdplot_rotated_coords/.append style={shift={(0,0,0)}}}} \newcommand {\tdplotsetthetaplanecoords }[1]{\tdplotresetrotatedcoordsorigin \tdplotsetrotatedcoords {270 + ##1}{270}{0}} \newcommand {\tdplotsetrotatedthetaplanecoords }[1]{\tdplotsetrotatedcoords {\tdplotalpha }{\tdplotbeta }{\tdplotgamma + ##1}\tikzset {tdplot_rotated_coords/.append style={y={(\raarc cm,\rbarc cm)},z={(\rabrc cm,\rbbrc cm)},x={(\racrc cm,\rbcrc cm)}}}} \newcommand {\tdplotsetcoord }[4]{\tdplotsinandcos {\sinthetavec }{\costhetavec }{##3}\tdplotsinandcos {\sinphivec }{\cosphivec }{##4}\tdplotmult {\stcpv }{\sinthetavec }{\cosphivec }\tdplotmult {\stspv }{\sinthetavec }{\sinphivec }\coordinate (##1) at ($##2*(\stcpv ,\stspv ,\costhetavec )$); \coordinate (##1xy) at ($##2*(\stcpv ,\stspv ,0)$); \coordinate (##1xz) at ($##2*(\stcpv ,0,\costhetavec )$); \coordinate (##1yz) at ($##2*(0,\stspv ,\costhetavec )$); \coordinate (##1x) at ($##2*(\stcpv ,0,0)$); \coordinate (##1y) at ($##2*(0,\stspv ,0)$); \coordinate (##1z) at ($##2*(0,0,\costhetavec )$); } \newcommand {\tdplotsimplesetcoord }[4]{\tdplotsinandcos {\sinthetavec }{\costhetavec }{##3}\tdplotsinandcos {\sinphivec }{\cosphivec }{##4}\tdplotmult {\stcpv }{\sinthetavec }{\cosphivec }\tdplotmult {\stspv }{\sinthetavec }{\sinphivec }\coordinate (##1) at ($##2*(\stcpv ,\stspv ,\costhetavec )$); } \newcommand {\tdplotsetpolarplotrange }[4]{\pgfmathsetmacro {\tdplotlowerphi }{##3} \pgfmathsetmacro {\tdplotupperphi }{##4} \pgfmathsetmacro {\tdplotlowertheta }{##1} \pgfmathsetmacro {\tdplotuppertheta }{##2} } \newcommand {\tdplotresetpolarplotrange }[0]{\pgfmathsetmacro {\tdplotlowerphi }{0} \pgfmathsetmacro {\tdplotupperphi }{360} \pgfmathsetmacro {\tdplotlowertheta }{0} \pgfmathsetmacro {\tdplotuppertheta }{180} } \newcommand {\tdplotdosurfaceplot }[6]{\par \pgfmathsetmacro {\nextphi }{\curphi + \tdplotsuperfudge *\viewphistep } \par \begin {scope}[opacity=1] \par \par \tdplotcheckdiff {\nextphi }{360}{\origviewphistep }{##2}{} \tdplotcheckdiff {\nextphi }{0}{\origviewphistep }{##2}{} \par \tdplotcheckdiff {\nextphi }{90}{\origviewphistep }{##3}{} \tdplotcheckdiff {\nextphi }{450}{\origviewphistep }{##3}{} \end {scope} \par \foreach \curtheta in{\viewthetastart ,\viewthetainc ,...,\viewthetaend } { \par \pgfmathsetmacro {\curlongitude }{90 -\curphi } \pgfmathsetmacro {\curlatitude }{90 -\curtheta } \par \ifthenelse {\equal {\leftright }{-1.0}}{\pgfmathsetmacro {\curphi }{\curphi -\origviewphistep } }{} \par \pgfmathsetmacro {\tdplottheta }{mod(\curtheta ,360)} \pgfmathsetmacro {\tdplotphi }{mod(\curphi ,360)} \par \pgfmathparse {\tdplotphi <0} \ifthenelse {\equal {\pgfmathresult }{1}}{ \pgfmathsetmacro {\tdplotphi }{\tdplotphi + 360} }{}\par \pgfmathparse {\tdplottheta >\tdplotuppertheta } \pgfmathsetmacro {\logictest }{1 -\pgfmathresult } \par \pgfmathparse {\tdplottheta <\tdplotlowertheta } \pgfmathsetmacro {\logictest }{\logictest * (1 -\pgfmathresult )} \par \pgfmathsetmacro {\tdplottheta }{\tdplottheta + \viewthetastep } \pgfmathparse {\tdplottheta >\tdplotuppertheta } \pgfmathsetmacro {\logictest }{\logictest * (1 -\pgfmathresult )} \par \pgfmathparse {\tdplottheta <\tdplotlowertheta } \pgfmathsetmacro {\logictest }{\logictest * (1 -\pgfmathresult )} \par \pgfmathparse {\tdplotphi >\tdplotupperphi } \pgfmathsetmacro {\logictest }{\logictest * (1 -\pgfmathresult )} \par \pgfmathparse {\tdplotphi <\tdplotlowerphi } \pgfmathsetmacro {\logictest }{\logictest * (1 -\pgfmathresult )} \par \pgfmathsetmacro {\tdplotphi }{\tdplotphi + \viewphistep } \par \pgfmathparse {\tdplotphi <0} \ifthenelse {\equal {\pgfmathresult }{1}}{ \pgfmathsetmacro {\tdplotphi }{\tdplotphi + 360} }{}\par \pgfmathparse {\tdplotphi >\tdplotupperphi } \pgfmathsetmacro {\logictest }{\logictest * (1 -\pgfmathresult )} \par \pgfmathparse {\tdplotphi <\tdplotlowerphi } \pgfmathsetmacro {\logictest }{\logictest * (1 -\pgfmathresult )} \par \par \pgfmathsetmacro {\tdplottheta }{\curtheta } \pgfmathsetmacro {\tdplotphi }{\curphi } \par \ifthenelse {\equal {##6}{parametricfill}}{\ifthenelse {\equal {\logictest }{1.0}}{\pgfmathsetmacro {\radius }{##1} \pgfmathsetmacro {\tdplotr }{\radius *360} \par \pgfmathlessthan {\radius }{0} \pgfmathsetmacro {\phaseshift }{180 * \pgfmathresult } \par \pgfmathsetmacro {\colorarg }{##5} \pgfmathsetmacro {\colorarg }{\colorarg + \phaseshift } \pgfmathsetmacro {\colorarg }{mod(\colorarg ,360)} \par \pgfmathlessthan {\colorarg }{0} \pgfmathsetmacro {\colorarg }{\colorarg + 360*\pgfmathresult } \par \pgfmathdivide {\colorarg }{360} \definecolor {tdplotfillcolor}{hsb}{\pgfmathresult ,1,1} \color {tdplotfillcolor} }{}}{\pgfsetfillcolor {##5} } \pgfsetstrokecolor {##4} \par \ifthenelse {\equal {\leftright }{-1.0}}{\pgfmathsetmacro {\curphi }{\curphi + \origviewphistep } }{} \par \ifthenelse {\equal {\logictest }{1.0}}{\pgfmathsetmacro {\radius }{abs(##1)} \pgfpathmoveto {\pgfpointspherical {\curlongitude }{\curlatitude }{\radius }} \par \pgfmathsetmacro {\tdplotphi }{\curphi + \viewphistep } \pgfmathsetmacro {\radius }{abs(##1)} \pgfpathlineto {\pgfpointspherical {\curlongitude -\viewphistep }{\curlatitude }{\radius }} \par \pgfmathsetmacro {\tdplottheta }{\curtheta + \viewthetastep } \pgfmathsetmacro {\radius }{abs(##1)} \pgfpathlineto {\pgfpointspherical {\curlongitude -\viewphistep }{\curlatitude -\viewthetastep }{\radius }} \par \pgfmathsetmacro {\tdplotphi }{\curphi } \pgfmathsetmacro {\radius }{abs(##1)} \pgfpathlineto {\pgfpointspherical {\curlongitude }{\curlatitude -\viewthetastep }{\radius }} \pgfpathclose \par \pgfusepath {fill,stroke} }{} } } \newcommand {\tdplotshowargcolorguide }[4]{ \par \pgfmathsetmacro {\tdplotx }{##1} \pgfmathsetmacro {\tdploty }{##2} \pgfmathsetmacro {\tdplothuestep }{5} \pgfmathsetmacro {\tdplotxsize }{##3} \pgfmathsetmacro {\tdplotysize }{##4} \par \pgfmathsetmacro {\tdplotyscale }{\tdplotysize /360} \par \foreach \tdplotphi in {0,\tdplothuestep ,...,360} { \pgfmathdivide {\tdplotphi }{360} \definecolor {tdplotfillcolor}{hsb}{\pgfmathresult ,1,1} \color {tdplotfillcolor} \par \pgfmathsetmacro {\tdplotstarty }{\tdploty + \tdplotphi * \tdplotyscale } \pgfmathsetmacro {\tdplotstopy }{\tdplotstarty + \tdplothuestep * \tdplotyscale } \pgfmathsetmacro {\tdplotstartx }{\tdplotx } \pgfmathsetmacro {\tdplotstopx }{\tdplotx + \tdplotxsize } \filldraw [tdplot_screen_coords] (\tdplotstartx ,\tdplotstarty ) rectangle (\tdplotstopx ,\tdplotstopy ); } \par \pgfmathsetmacro {\tdplotstopy }{\tdploty + (360+\tdplothuestep )*\tdplotyscale } \pgfmathsetmacro {\tdplotstopx }{\tdplotx + \tdplotxsize } \par \draw [tdplot_screen_coords] (\tdplotx ,\tdploty ) rectangle (\tdplotstopx ,\tdplotstopy ); \par \node [tdplot_screen_coords,anchor=west,xshift=5pt] at (\tdplotstopx ,\tdploty ) {$0$}; \node [tdplot_screen_coords,anchor=west,xshift=5pt] at (\tdplotstopx ,\tdplotstopy ) {$2\pi $}; \par \pgfmathsetmacro {\tdplotstopy }{\tdploty + (360+\tdplothuestep )/2*\tdplotyscale } \node [tdplot_screen_coords,anchor=west,xshift=5pt] at (\tdplotstopx ,\tdplotstopy ) {$\pi $}; } \newcommand {\tdplotgetpolarcoords }[3]{\pgfmathsetmacro {\vxcalc }{##1} \pgfmathsetmacro {\vycalc }{##2} \pgfmathsetmacro {\vzcalc }{##3} \pgfmathsetmacro {\vcalc }{ sqrt((\vxcalc )^2 + (\vycalc )^2 + (\vzcalc )^2) } \par \pgfmathsetmacro {\vxycalc }{ sqrt((\vxcalc )^2 + (\vycalc )^2) } \par \pgfmathsetmacro {\tdplotrestheta }{asin(\vxycalc /\vcalc )} \pgfmathparse {\vzcalc <0} \ifthenelse {\equal {\pgfmathresult }{1}}{\pgfmathsetmacro {\tdplotrestheta }{180 -\tdplotrestheta } } {} \ifthenelse {\equal {\vxcalc }{0.0}}{\pgfmathparse {\vycalc <0} \ifthenelse {\equal {\pgfmathresult }{1}}{\pgfmathsetmacro {\tdplotresphi }{270} } {\pgfmathparse {\vycalc >0} \ifthenelse {\equal {\pgfmathresult }{1}}{\pgfmathsetmacro {\tdplotresphi }{90} } {\pgfmathsetmacro {\tdplotresphi }{0} } } } {\pgfmathsetmacro {\tdplotresphi }{atan(\vycalc /\vxcalc )} \pgfmathparse {\vxcalc <0} \ifthenelse {\equal {\pgfmathresult }{1}}{\pgfmathsetmacro {\tdplotresphi }{\tdplotresphi +180} } { } \par \pgfmathparse {\tdplotresphi <0} \ifthenelse {\equal {\pgfmathresult }{1}}{\pgfmathsetmacro {\tdplotresphi }{\tdplotresphi +360} } {} } } \newcommand {\vec }[1]{\mathbf {##1}} \newcommand {\RR }[0]{\mathbb {R}} \newcommand {\dfn }[0]{\textit } \newcommand {\dotp }[0]{\cdot } \newcommand {\id }[0]{\text {id}} \newcommand {\norm }[1]{\left \lVert ##1\right \rVert } \newcommand {\dst }[0]{\displaystyle } \newcommand {\MHPrecedingSpacesOff }[0]{\MH_let:NwN \@xargdef \MH_nospace_xargdef:nwwn } \newcommand {\MHPrecedingSpacesOn }[0]{\MH_let:NwN \@xargdef \MH_kernel_xargdef:nwwn } \newcommand {\mathtoolsset }[1]{\setkeys {\MT_options_name: }{##1}} \newcommand {\newtagform }[1]{\@ifundefined {MT_tagform_##1:n}{\@ifnextchar [{\MT_define_tagform:nwnn ##1}{\MT_define_tagform:nwnn ##1[]}}{\PackageError {mathtools}{The tag form ‘##1’is already defined\MessageBreak You probably want to look up \@backslashchar renewtagform instead}{I will just ignore your wish for now.}}} \newcommand {\renewtagform }[1]{\@ifundefined {MT_tagform_##1:n}{\PackageError {mathtools}{The tag form ‘##1’is not defined\MessageBreak You probably want to look up \@backslashchar newtagform instead}{I will just ignore your wish for now.}}{\@ifnextchar [{\MT_define_tagform:nwnn ##1}{\MT_define_tagform:nwnn ##1[]}}} \newcommand {\usetagform }[1]{\@ifundefined {MT_tagform_##1:n}{\PackageError {mathtools}{You have chosen the tag form ‘##1’\MessageBreak but it appears to be undefined}{I will use the default tag form instead.}\@namedef {tagform@}{\@nameuse {MT_tagform_default:n}}}{\@namedef {tagform@}{\@nameuse {MT_tagform_##1:n}}}\MH_if_boolean:nT {show_only_refs}{\MH_let:NwN \MT_prev_tagform:n \tagform@ \def \tagform@ ####1{\MT_extended_tagform:n {####1}}}} \newcommand {\refeq }[1]{\textup {\ref {##1}}} \newcommand {\MT@newlabel }[1]{\global \@namedef {MT_r_##1}{}} \newcommand {\MT_showonlyrefs_true: }[0]{\MH_if_boolean:nF {show_only_refs}{\MH_set_boolean_T:n {show_only_refs}\MH_let:NwN \MT_incr_eqnum: \incr@eqnum \MH_let:NwN \incr@eqnum \@empty \MH_let:NwN \MT_array_parbox_restore: \@arrayparboxrestore \@xp \def \@xp \@arrayparboxrestore \@xp {\@arrayparboxrestore \MH_let:NwN \incr@eqnum \@empty }\MH_let:NwN \MT_prev_tagform:n \tagform@ \MH_let:NwN \MT_eqref:n \eqref \MH_let:NwN \MT_refeq:n \refeq \MH_let:NwN \MT_maketag:n \maketag@@@ \MH_let:NwN \maketag@@@ \MT_extended_maketag:n \def \tagform@ ####1{\MT_extended_tagform:n {####1}}\MH_let:NwN \eqref \MT_extended_eqref:n \MH_let:NwN \refeq \MT_extended_refeq:n }} \newcommand {\nonumber }[0]{\if@eqnsw \MH_if_meaning:NN \incr@eqnum \@empty \MH_if_boolean:nF {show_only_refs}{\addtocounter {equation}\m@ne }\MH_fi: \MH_fi: \MH_let:NwN \print@eqnum \@empty \MH_let:NwN \incr@eqnum \@empty \global \@eqnswfalse } \newcommand {\noeqref }[1]{\@bsphack \@for \@tempa :=##1\do {\@safe@activestrue \edef \@tempa {\expandafter \@firstofone \@tempa }\@ifundefined {r@\@tempa }{\protect \G@refundefinedtrue \@latex@warning {Reference ‘\@tempa ’on page \thepage \space undefined (\string \noeqref )}}{}\if@filesw \protected@write \@auxout {}{\string \MT@newlabel {\@tempa }}\fi \@safe@activesfalse }\@esphack } \newcommand {\reserved@a }[0]{} \newcommand {\reserved@a }[0]{} \newcommand {\underbracket }[0]{\@ifnextchar [{\MT_underbracket_I:w }{\MT_underbracket_I:w [\l_MT_bracketheight_fdim ]}} \newcommand {\overbracket }[0]{\@ifnextchar [{\MT_overbracket_I:w }{\MT_overbracket_I:w [\l_MT_bracketheight_fdim ]}} \newcommand {\lparen }[0]{(} \newcommand {\rparen }[0]{)} \newcommand {\ordinarycolon }[0]{:} \newcommand {\MT_test_for_tcb_other:nnnnn }[1]{\MH_if:w t##1\relax \expandafter \MH_use_choice_i:nnnn \MH_else: \MH_if:w c##1\relax \expandafter \expandafter \expandafter \MH_use_choice_ii:nnnn \MH_else: \MH_if:w b##1\relax \expandafter \expandafter \expandafter \expandafter \expandafter \expandafter \expandafter \MH_use_choice_iii:nnnn \MH_else: \expandafter \expandafter \expandafter \expandafter \expandafter \expandafter \expandafter \MH_use_choice_iv:nnnn \MH_fi: \MH_fi: \MH_fi: } \newcommand {\MT_start_mult:N }[1]{\MT_test_for_tcb_other:nnnnn {##1}{\MH_let:NwN \MT_next: \vtop }{\MH_let:NwN \MT_next: \vcenter }{\MH_let:NwN \MT_next: \vbox }{\PackageError {mathtools}{Invalid position specifier. I’ll try to recover with ‘c’}\@ehc }\collect@body \MT_mult_internal:n } \newcommand {\MT_mult_internal:n }[1]{\MH_if_boolean:nF {outer_mult}{\alignedspace@left }\MT_next: \bgroup \Let@ \def \l_MT_multline_lastline_fint {0}\chardef \dspbrk@context \@ne \restore@math@cr \MH_let:NwN \math@cr@@ \MT_mult_mathcr_atat:w \MH_let:NwN \shoveleft \MT_shoveleft:wn \MH_let:NwN \shoveright \MT_shoveright:wn \spread@equation \MH_set_boolean_F:n {mult_firstline}\MT_measure_mult:n {##1}\MH_if_dim:w \l_MT_multwidth_dim <\l_MT_multline_measure_fdim \MH_setlength:dn \l_MT_multwidth_dim {\l_MT_multline_measure_fdim }\fi \MH_set_boolean_T:n {mult_firstline}\MH_if_num:w \l_MT_multline_lastline_fint =\@ne \MH_let:NwN \math@cr@@ \MT_mult_firstandlast_mathcr:w \MH_fi: \ialign \bgroup \hfil \strut@ $\m@th \displaystyle {}####$\hfil \crcr \hfilneg ##1} \newcommand {\MT_measure_mult:n }[1]{\begingroup \measuring@true \g_MT_multlinerow_int \@ne \MH_let:NwN \label \MT_gobblelabel:w \MH_let:NwN \tag \gobble@tag \setbox \z@ \vbox {\ialign {\strut@ $\m@th \displaystyle {}####$\crcr ##1\crcr }}\xdef \l_MT_multline_measure_fdim {\the \wdz@ }\advance \g_MT_multlinerow_int \m@ne \xdef \l_MT_multline_lastline_fint {\number \g_MT_multlinerow_int }\endgroup \g_MT_multlinerow_int \@ne } \newcommand {\MultlinedHook }[0]{\renewenvironment {subarray}[1]{\vcenter \bgroup \Let@ \restore@math@cr \default@tag \let \math@cr@@ \AMS@math@cr@@ \baselineskip \fontdimen 10\scriptfont \tw@ \advance \baselineskip \fontdimen 12\scriptfont \tw@ \lineskip \thr@@ \fontdimen 8\scriptfont \thr@@ \lineskiplimit \lineskip \ialign \bgroup \ifx c####1\hfil \fi $\m@th \scriptstyle ########$\hfil \crcr }{\crcr \egroup \egroup }} \newcommand {\MT_delim_default_inner_wrappers:n }[1]{\@namedef {MT_delim_\MH_cs_to_str:N ##1_star_wrapper:nnn}####1####2####3{\mathopen {}\mathclose \bgroup ####1####2\aftergroup \egroup ####3}\@namedef {MT_delim_\MH_cs_to_str:N ##1_nostarscaled_wrapper:nnn}####1####2####3{\mathopen {####1}####2\mathclose {####3}}\@namedef {MT_delim_\MH_cs_to_str:N ##1_nostarnonscaled_wrapper:nnn}####1####2####3{\mathopen ####1####2\mathclose ####3}} \newcommand {\reDeclarePairedDelimiterInnerWrapper }[3]{\@ifundefined {MT_delim_\MH_cs_to_str:N ##1_##2_wrapper:nnn}{\PackageError {mathtools}{Wrapper not found for \string ##1 and option ’##2’.\MessageBreak Either \string ##1 is not defined,or you are using the \MessageBreak ’nostar’option,which is no longer supported. \MessageBreak Please use ’nostarnonscaled’or ’nostarscaled \MessageBreak instead. }{Seethemanual}}{\@namedef {MT_delim_\MH_cs_to_str:N ##1_##2_wrapper:nnn}####1####2####3{##3}}} \newcommand {\DeclarePairedDelimiter }[3]{\@ifdefinable {##1}{\MT_delim_default_inner_wrappers:n {##1}\@namedef {MT_delim_\MH_cs_to_str:N ##1_star:}####1{\@nameuse {MT_delim_\MH_cs_to_str:N ##1_star_wrapper:nnn}{\left ##2}{####1}{\right ##3}}\@xp \@xp \@xp \newcommand \@xp \csname MT_delim_\MH_cs_to_str:N ##1_nostar:\endcsname [2][\\@gobble]{\def \@tempa {\\@gobble}\def \@tempb {####1}\ifx \@tempa \@tempb \@nameuse {MT_delim_\MH_cs_to_str:N ##1_nostarnonscaled_wrapper:nnn}{##2}{####2}{##3}\else \MT_etb_ifblank:nnn {####1}{\@nameuse {MT_delim_\MH_cs_to_str:N ##1_nostarnonscaled_wrapper:nnn}{##2}{####2}{##3}}{\@nameuse {MT_delim_\MH_cs_to_str:N ##1_nostarscaled_wrapper:nnn}{\@nameuse {\MH_cs_to_str:N ####1l}##2}{####2}{\@nameuse {\MH_cs_to_str:N ####1r}##3}}\fi }\DeclareRobustCommand {##1}{\@ifstar {\@nameuse {MT_delim_\MH_cs_to_str:N ##1_star:}}{\@nameuse {MT_delim_\MH_cs_to_str:N ##1_nostar:}}}}} \newcommand {\MT_delim_inner_generator:nnnnnnn }[7]{\@xp \@xp \@xp \newcommand \@xp \csname MT_delim_\MH_cs_to_str:N ##1_nostar_inner:\endcsname [##2]{##3\def \@tempa {\@MHempty }\@xp \def \@xp \@tempb \@xp {\delimsize }\ifx \@tempa \@tempb \@nameuse {MT_delim_\MH_cs_to_str:N ##1_nostarnonscaled_wrapper:nnn}{##4}{##7}{##5}\else \MT_etb_ifdefempty_x:nnn {\delimsize }{\@nameuse {MT_delim_\MH_cs_to_str:N ##1_nostarnonscaled_wrapper:nnn}{##4}{##7}{##5}}{\@nameuse {MT_delim_\MH_cs_to_str:N ##1_nostarscaled_wrapper:nnn}{\@xp \@xp \@xp \csname \@xp \MH_cs_to_str:N \delimsize l\endcsname ##4}{##7}{\@xp \@xp \@xp \csname \@xp \MH_cs_to_str:N \delimsize r\endcsname ##5}}\fi ##6\endgroup }} \newcommand {\newcases }[6]{\newenvironment {##1}{\MT_start_cases:nnnn {##2}{##3}{##4}{##5}}{\MH_end_cases: \right ##6}} \newcommand {\renewcases }[6]{\renewenvironment {##1}{\MT_start_cases:nnnn {##2}{##3}{##4}{##5}}{\MH_end_cases: \right ##6}} \newcommand {\dcases }[0]{\MT_start_cases:nnnn {\quad }{$\m@th \displaystyle {####}$\hfil }{$\m@th \displaystyle {####}$\hfil }{\lbrace }} \newcommand {\dcases* }[0]{\MT_start_cases:nnnn {\quad }{$\m@th \displaystyle {####}$\hfil }{{####}\hfil }{\lbrace }} \newcommand {\rcases }[0]{\MT_start_cases:nnnn {\quad }{$\m@th {####}$\hfil }{$\m@th {####}$\hfil }{.}} \newcommand {\rcases* }[0]{\MT_start_cases:nnnn {\quad }{$\m@th {####}$\hfil }{{####}\hfil }{.}} \newcommand {\drcases }[0]{\MT_start_cases:nnnn {\quad }{$\m@th \displaystyle {####}$\hfil }{$\m@th \displaystyle {####}$\hfil }{.}} \newcommand {\drcases* }[0]{\MT_start_cases:nnnn {\quad }{$\m@th \displaystyle {####}$\hfil }{{####}\hfil }{.}} \newcommand {\cases* }[0]{\MT_start_cases:nnnn {\quad }{$\m@th {####}$\hfil }{{####}\hfil }{\lbrace }} \newcommand {\psmallmatrix }[0]{\@nameuse {psmallmatrixhook}\mathopen {}\mathclose \bgroup \left (\MT_smallmatrix_begin:N c} \newcommand {\bsmallmatrix }[0]{\@nameuse {bsmallmatrixhook}\mathopen {}\mathclose \bgroup \left [\MT_smallmatrix_begin:N c} \newcommand {\Bsmallmatrix }[0]{\@nameuse {Bsmallmatrixhook}\mathopen {}\mathclose \bgroup \left \lbrace \MT_smallmatrix_begin:N c} \newcommand {\vsmallmatrix }[0]{\@nameuse {vsmallmatrixhook}\mathopen {}\mathclose \bgroup \left \lvert \MT_smallmatrix_begin:N c} \newcommand {\Vsmallmatrix }[0]{\@nameuse {Vsmallmatrixhook}\mathopen {}\mathclose \bgroup \left \lVert \MT_smallmatrix_begin:N c} \newcommand {\adjustlimits }[6]{\sbox \z@ {$\m@th \displaystyle ##1$}\sbox \tw@ {$\m@th \displaystyle ##4$}\@tempdima =\dp \z@ \advance \@tempdima -\dp \tw@ \MH_if_dim:w \@tempdima >\z@ \mathop {##1}\limits ##2{##3}\MH_else: \mathop {##1\MT_vphantom:Nn \displaystyle {##4}}\limits ##2{\def \finsm@sh {\ht \z@ \z@ \box \z@ }\mathsm@sh \scriptstyle {\MT_cramped_internal:Nn \scriptstyle {##3}}\MT_vphantom:Nn \scriptstyle {\MT_cramped_internal:Nn \scriptstyle {##6}}}\MH_fi: \MH_if_dim:w \@tempdima >\z@ \mathop {##4\MT_vphantom:Nn \displaystyle {##1}}\limits ##5{\MT_vphantom:Nn \scriptstyle {\MT_cramped_internal:Nn \scriptstyle {##3}}\def \finsm@sh {\ht \z@ \z@ \box \z@ }\mathsm@sh \scriptstyle {\MT_cramped_internal:Nn \scriptstyle {##6}}}\MH_else: \mathop {##4}\limits ##5{##6}\MH_fi: } \newcommand {\SwapAboveDisplaySkip }[0]{\noalign {\vskip -\abovedisplayskip \vskip \abovedisplayshortskip }} \newcommand {\Aboxed }[1]{\let \bgroup {\romannumeral -‘}\@Aboxed ##1&&\ENDDNE } \newcommand {\vdotswithin }[1]{{\mathmakebox [\widthof {\ensuremath {{}##1{}}}][c]{{\vdots }}}} \newcommand {\MTFlushSpaceAbove }[0]{\expandafter \MT_remove_tag_unless_inner:n \expandafter {\@currenvir }\\\noalign {\nobreak \vskip -\baselineskip \vskip -\lineskip \vskip -\l_MT_shortvdotswithinadjustabove_dim \vskip -\origjot \vskip \jot }\noalign {\expandafter \MT_remove_tag_unless_inner:n \expandafter {\@currenvir }}} \newcommand {\MTFlushSpaceBelow }[0]{\\\noalign {\nobreak \vskip -\lineskip \vskip -\l_MT_shortvdotswithinadjustbelow_dim \vskip -\origjot \vskip \jot }} \newcommand {\shortintertext }[0]{\@amsmath@err {\Invalid@@ \shortintertext }\@eha } \newcommand {\clap }[1]{\hb@xt@ \z@ {\hss ##1\hss }} \newcommand {\mathmbox }[0]{\mathpalette \MT_mathmbox:nn } \newcommand {\mathmakebox }[0]{\@ifnextchar [\MT_mathmakebox_I:w \mathmbox } \newcommand {\MT_prescript_inner: }[4]{\@mathmeasure \z@ ##4{\MT_prescript_sup: {##1}}\@mathmeasure \tw@ ##4{\MT_prescript_sub: {##2}}\MH_if_dim:w \wd \tw@ >\wd \z@ \setbox \z@ \hbox to\wd \tw@ {\hfil \unhbox \z@ }\MH_else: \setbox \tw@ \hbox to\wd \z@ {\hfil \unhbox \tw@ }\MH_fi: \mathop {}\mathopen {\vphantom {\MT_prescript_arg: {##3}}}^{\box \z@ }\sb {\box \tw@ }\MT_prescript_arg: {##3}} \newcommand {\prescript }[3]{\mathchoice {\MT_prescript_inner: {##1}{##2}{##3}{\scriptstyle }}{\MT_prescript_inner: {##1}{##2}{##3}{\scriptstyle }}{\MT_prescript_inner: {##1}{##2}{##3}{\scriptscriptstyle }}{\MT_prescript_inner: {##1}{##2}{##3}{\scriptscriptstyle }}} \newcommand {\spreadlines }[1]{\setlength {\jot }{##1}\ignorespaces } \newcommand {\newgathered }[4]{\newenvironment {##1}{\def \MT_gathered_pre: {##2}\def \MT_gathered_post: {##3}\def \MT_gathered_env_end: {##4}\MT_gathered_env }{\endMT_gathered_env }} \newcommand {\renewgathered }[4]{\renewenvironment {##1}{\def \MT_gathered_pre: {##2}\def \MT_gathered_post: {##3}\def \MT_gathered_env_end: {##4}\MT_gathered_env }{\endMT_gathered_env }} \newcommand {\lgathered }[0]{\def \MT_gathered_pre: {}\def \MT_gathered_post: {\hfil }\def \MT_gathered_env_end: {}\MT_gathered_env } \newcommand {\rgathered }[0]{\def \MT_gathered_pre: {\hfil }\def \MT_gathered_post: {}\def \MT_gathered_env_end: {}\MT_gathered_env } \newcommand {\gathered }[0]{\def \MT_gathered_pre: {\hfil }\def \MT_gathered_post: {\hfil }\def \MT_gathered_env_end: {}\MT_gathered_env } \newcommand {\splitfrac }[2]{\genfrac {}{}{0pt}{1}{\textstyle ##1\quad \hfill }{\textstyle \hfill \quad \mathstrut ##2}} \newcommand {\splitdfrac }[2]{\genfrac {}{}{0pt}{0}{##1\quad \hfill }{\hfill \quad \mathstrut ##2}} \newcommand {\reserved@a }[2]{} \newcommand {\HyperFirstAtBeginDocument }[0]{\AtBeginDocument } \newcommand {\reserved@a }[1]{} \newcommand {\reserved@a }[2]{} \newcommand {\vnameref }[1]{\unskip ~\nameref {##1}\@vpageref [\unskip ]{##1}} \newcommand {\ref }[0]{\@ifstar \@refstar \T@ref } \newcommand {\pageref }[0]{\@ifstar \@pagerefstar \T@pageref } \newcommand {\nameref }[0]{\@ifstar \@namerefstar \T@nameref } \newcommand {\dblcolon }[0]{\vcentcolon \mathrel {\mkern -.9mu}\vcentcolon } \newcommand {\coloneqq }[0]{\vcentcolon \mathrel {\mkern -1.2mu}=} \newcommand {\Coloneqq }[0]{\dblcolon \mathrel {\mkern -1.2mu}=} \newcommand {\coloneq }[0]{\vcentcolon \mathrel {\mkern -1.2mu}\mathrel {-}} \newcommand {\Coloneq }[0]{\dblcolon \mathrel {\mkern -1.2mu}\mathrel {-}} \newcommand {\eqqcolon }[0]{=\mathrel {\mkern -1.2mu}\vcentcolon } \newcommand {\Eqqcolon }[0]{=\mathrel {\mkern -1.2mu}\dblcolon } \newcommand {\eqcolon }[0]{\mathrel {-}\mathrel {\mkern -1.2mu}\vcentcolon } \newcommand {\Eqcolon }[0]{\mathrel {-}\mathrel {\mkern -1.2mu}\dblcolon } \newcommand {\colonapprox }[0]{\vcentcolon \mathrel {\mkern -1.2mu}\approx } \newcommand {\Colonapprox }[0]{\dblcolon \mathrel {\mkern -1.2mu}\approx } \newcommand {\colonsim }[0]{\vcentcolon \mathrel {\mkern -1.2mu}\sim } \newcommand {\Colonsim }[0]{\dblcolon \mathrel {\mkern -1.2mu}\sim } \newcommand {\nuparrow }[0]{\MH_nuparrow: } \newcommand {\ndownarrow }[0]{\MH_ndownarrow: } \newcommand {\bigtimes }[0]{\MH_csym_bigtimes: } \newcommand {\reserved@a }[2]{} \newcommand {\reserved@a }[0]{\AtBeginDocument } \newcommand {\reserved@a }[1]{} \newcommand {\reserved@a }[2]{}$

Mixing Problems

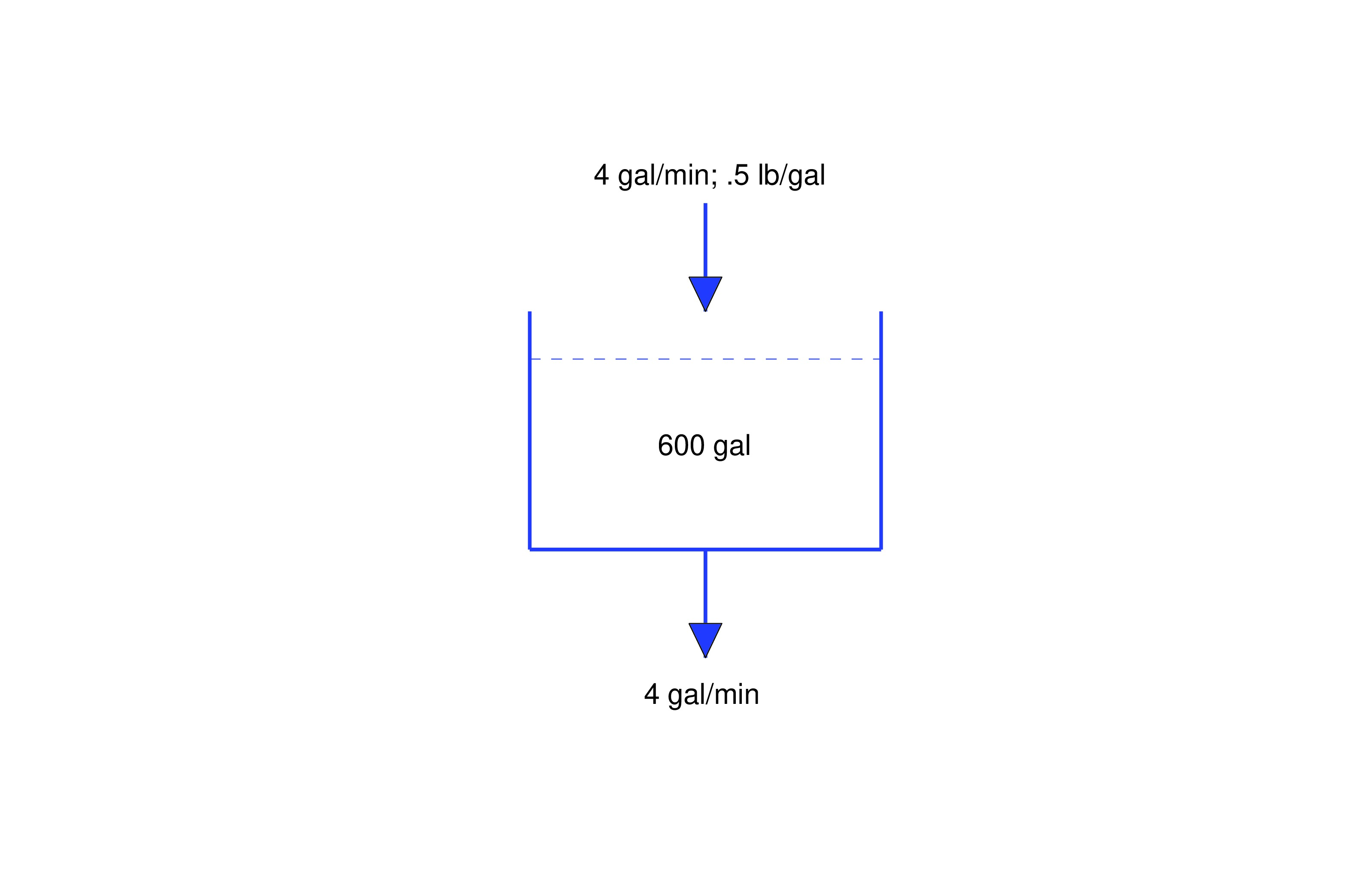
In the next two examples a saltwater solution with a given concentration (weight of salt per unit volume of solution) is added at a specified rate to a tank that initially contains saltwater with a different concentration. The problem is to determine the quantity of salt in the tank as a function of time. This is an example of a mixing problem. To construct a tractable mathematical model for mixing problems we assume in our examples (and most exercises) that the mixture is stirred instantly so that the salt is always uniformly distributed throughout the mixture. Several exercises will deal with situations where this isn’t so, but the distribution of salt becomes approximately uniform as $t\to \infty$ .

A tank initially contains $40$ pounds of salt dissolved in 600 gallons of water. Starting at $t_0 = 0$ , water that contains $1/2$ pound of salt per gallon is poured into the tank at the rate of $4$ gal/min and the mixture is drained from the tank at the same rate, as shown in the figure.

(a): Find a differential equation for the quantity $Q(t)$ of salt in the tank at time $t > 0$ , and solve the equation to determine $Q(t)$ .
(b): Find $\lim _{t\rightarrow \infty }Q(t)$ .

item:4.2.3a To find a differential equation for $Q$ , we must use the given information to derive an expression for $Q'$ . But $Q'$ is the rate of change of the quantity of salt in the tank changes with respect to time; thus, if rate in denotes the rate at which salt enters the tank and rate out denotes the rate by which it leaves, then $\begin{equation} \label{eq:4.2.5} Q' = \mbox{rate in}-\mbox{rate out}. \end{equation}$ The rate in is $\left (\frac {1}{2}\ \mbox {lb/gal}\right ) \times (4\ \mbox {gal/min}) = 2\ \mbox {lb/min}.$ Determining the rate out requires a little more thought. We’re removing $4$ gallons of the mixture per minute, and there are always $600$ gallons in the tank; that is, we’re removing $1/150$ of the mixture per minute. 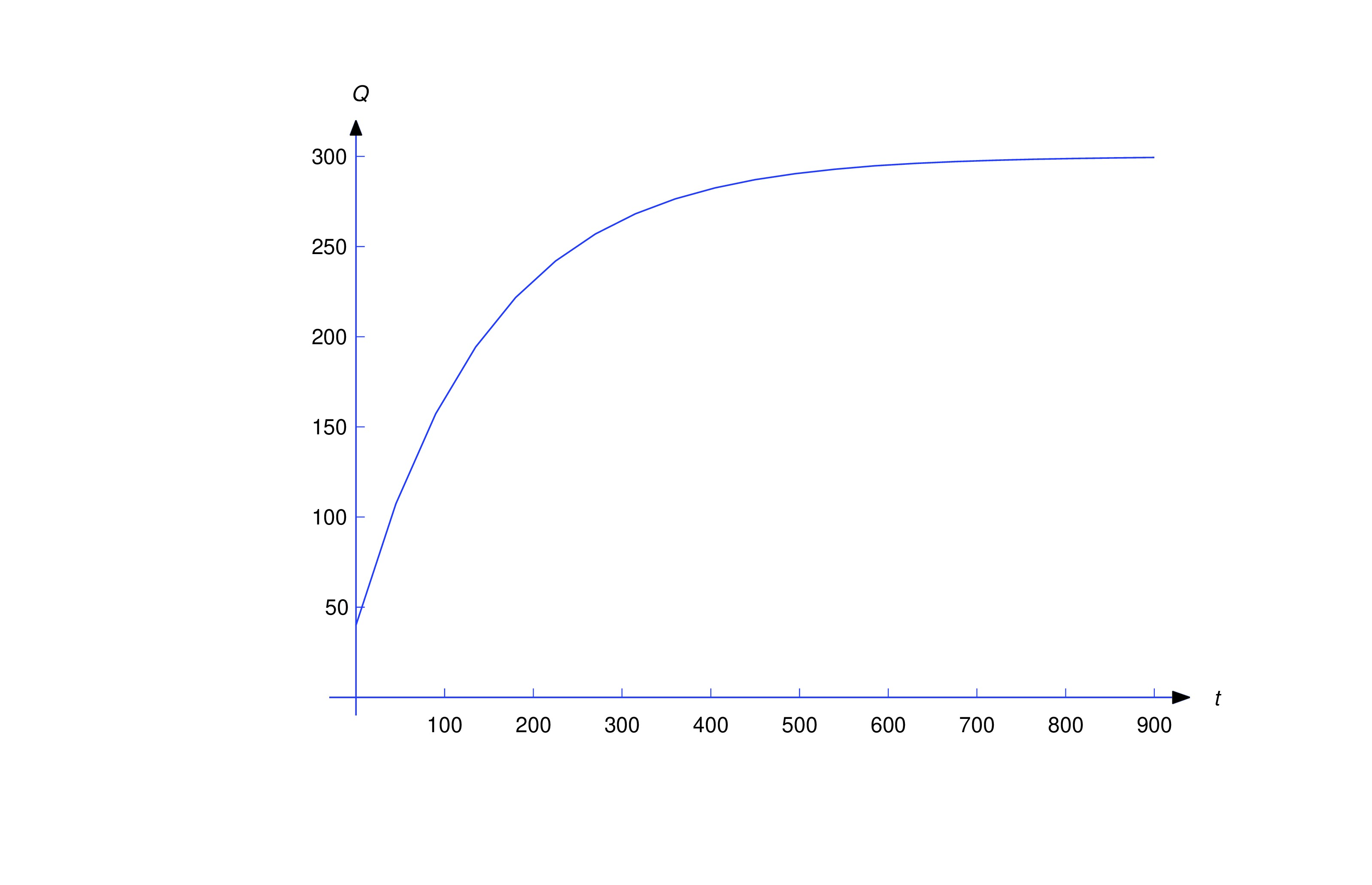Since the salt is evenly distributed in the mixture, we are also removing $1/150$ of the salt per minute. Therefore, if there are $Q(t)$ pounds of salt in the tank at time $t$ , the rate out at any time $t$ is $Q(t)/150$ . Alternatively, we can arrive at this conclusion by arguing that $\begin {array}{lcl} \mbox {rate out} & = & (\mbox {concentration})\times (\mbox {rate of flow out})\\ \mbox {}&=&(\mbox {lb/gal})\times (\mbox {gal/min})\\ &=&\frac {Q(t)}{600}\times 4=\frac {Q(t)}{150} \end {array}$ We can now write (eq:4.2.5) as $Q' = 2-\frac {Q}{150}.$ This first order equation can be rewritten as $Q'+\frac {Q}{150} = 2.$ Since $e^{-t/150}$ is a solution of the complementary equation, the solutions of this equation are of the form $Q=ue^{-t/150}$ , where $u'e^{-t/150}=2$ , so $u'=2e^{t/150}$ . Hence, $u = 300e^{t/150}+c,$ so $\begin{equation} \label{eq:4.2.6} Q=ue^{-t/150}=300+ce^{-t/150} \end{equation}$ See the graph of $Q$ in the figure below.

Since $Q(0)=40$ , $c=-260$ ; therefore, $Q=300-260e^{-t/150}.$

item:4.2.3b From (eq:4.2.6), we see that that $\lim _{t \rightarrow \infty }Q(t)=300$ for any value of $Q(0)$ . This is intuitively reasonable, since the incoming solution contains $1/2$ pound of salt per gallon and there are always 600 gallons of water in the tank.

A $500$ -liter tank initially contains $10$ g of salt dissolved in $200$ liters of water. Starting at $t_0=0$ , water that contains $1/4$ g of salt per liter is poured into the tank at the rate of $4$ liters/min and the mixture is drained from the tank at the rate of $2$ liters/min, as shown in the figure below.

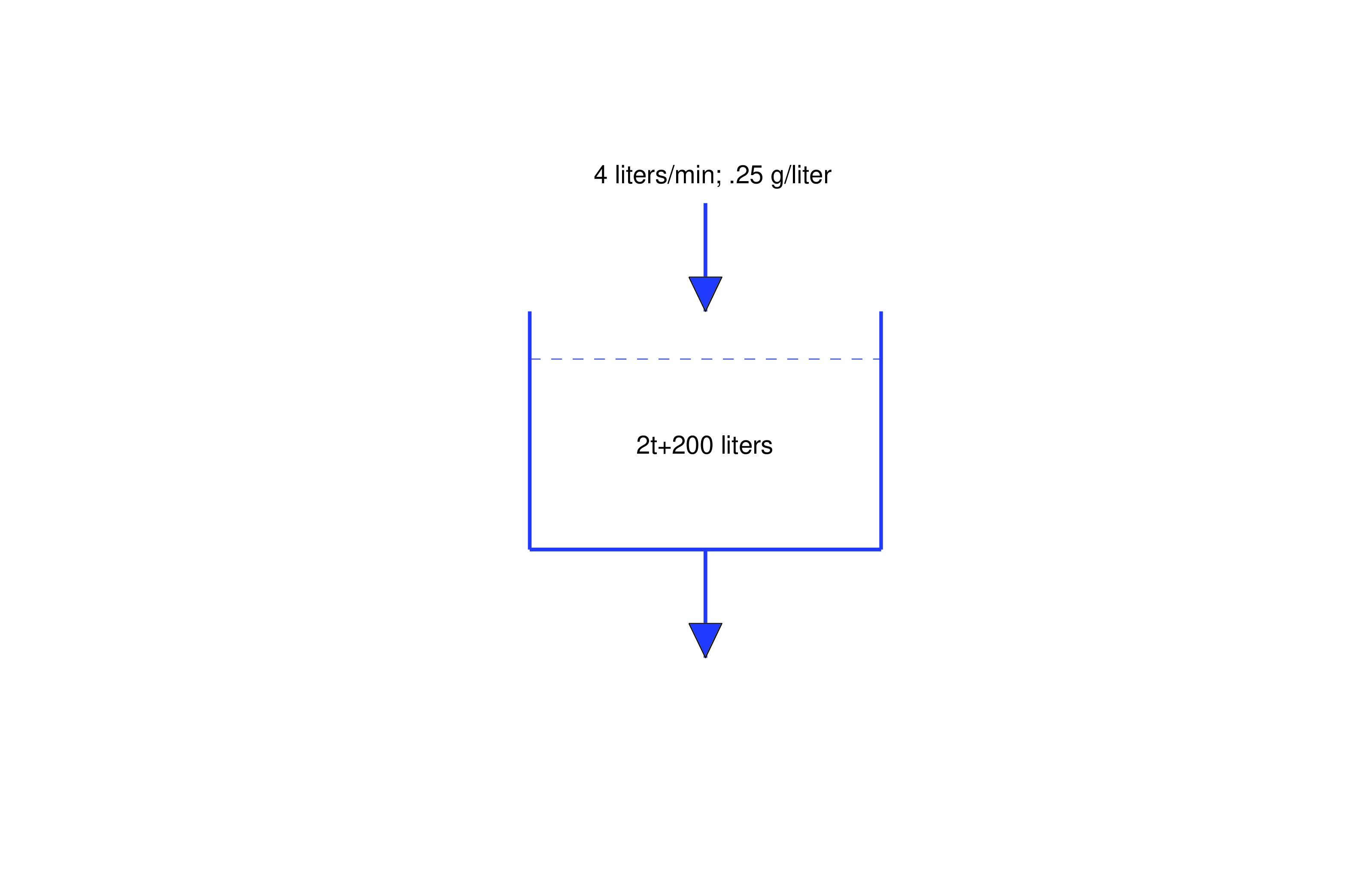
When will the tank overflow? $t=\answer {150}$ minutes.

Find a differential equation for the quantity $Q(t)$ of salt in the tank at time $t$ prior to the time when the tank overflows and find the concentration $K(t)$ (g/liter ) of salt in the tank at any such time.

We first determine the amount $W(t)$ of solution in the tank at any time $t$ prior to overflow. Since $W(0) = 200$ and we’re adding $4$ liters/min while removing only $2$ liters/min, there’s a net gain of $2$ liters/min in the tank; therefore, $W(t) = 2t+200.$ Since $W(150)=500$ liters (capacity of the tank), this formula is valid for $0 \leq t \leq 150$ .

Now let $Q(t)$ be the number of grams of salt in the tank at time $t$ , where $0 \leq t \leq 150$ . As in Example example:4.2.3,

$\begin{equation} \label{eq:4.2.7} Q' = \mbox{rate in}-\mbox{rate out}. \end{equation}$ The rate in is $\begin{equation} \label{eq:4.2.8} \left(\frac{1}{4}\ \mbox{g/liter}\,\right) \times (4\ \mbox{liters/min}\,) = 1\ \mbox{g/min}. \end{equation}$ To determine the rate out, we observe that since the mixture is being removed from the tank at the constant rate of $2$ liters/min and there are $2t+200$ liters in the tank at time $t$ , the fraction of the mixture being removed per minute at time $t$ is $\frac {2}{2t+200} = \frac {1}{t+100}.$ We’re removing this same fraction of the salt per minute. Therefore, since there are $Q(t)$ grams of salt in the tank at time $t$ , $\begin{equation} \label{eq:4.2.9} \mbox{rate out} = \frac{Q(t)}{t+100}. \end{equation}$ Alternatively, we can arrive at this conclusion by arguing that $\begin {array}{lcl} \mbox {rate out} & = & (\mbox {concentration})\times (\mbox {rate of flow out}) =(\mbox {g/liter})\times (\mbox {liters/min})\\ &=&\frac {Q(t)}{2t+200}\times 2=\frac {Q(t)}{t+100}. \end {array}$ Substituting (eq:4.2.8) and (eq:4.2.9) into (eq:4.2.7) yields $\begin{equation} \label{eq:4.2.10} Q'=1-\frac{Q}{t+100},\quad\text{ so }\quad Q'+\frac{1}{t+100} Q=1. \end{equation}$ By separation of variables, $1/(t+100)$ is a solution of the complementary equation, so the solutions of (eq:4.2.10) are of the form $Q=\frac {u}{t+100},\quad \mbox {where}\quad \frac {u'}{t+100}=1,\quad \mbox {so}\quad u'=t+100.$ Hence, $\begin{equation} \label{eq:4.2.11} u = \frac{(t+100)^2}{2}+c. \end{equation}$ Since $Q(0)=10$ and $u=(t+100)Q$ , (eq:4.2.11) implies that $(100)(10) = \frac {(100)^2}{2}+c,$ so $c=100(10)-\frac {(100)^2}{2} =-4000$ and therefore $u = \frac {(t+100)^2}{2} -4000.$ Hence, $Q = \frac {u}{t+200}= \frac {t+100}{2}-\frac {4000}{t+100}.$ Now let $K(t)$ be the concentration of salt at time $t$ . Then $K(t) = \frac {1}{4}-\frac {2000}{(t+100)^2}$ The graph of $K$ is shown below.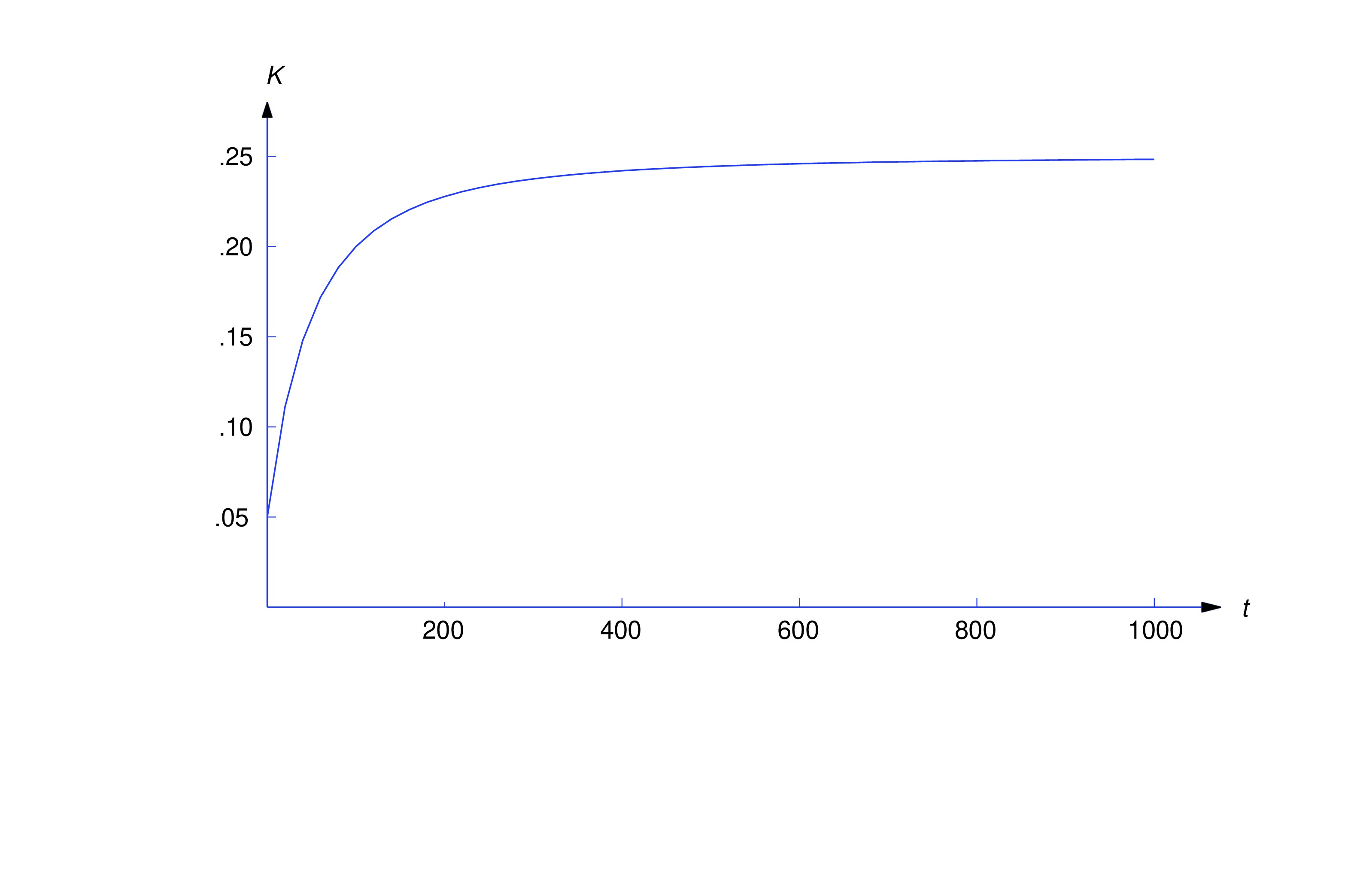

Text Source

Trench, William F., ”Elementary Differential Equations” (2013). Faculty Authored and Edited Books & CDs. 8. (CC-BY-NC-SA)

https://digitalcommons.trinity.edu/mono/8/