We demonstrate how Laplace transforms can be used to solve constant coefficient second order initial value problems.
Solution of Initial Value Problems
Laplace Transforms of Derivatives
In the rest of this chapter we’ll use the Laplace transform to solve initial value problems for constant coefficient second order equations. To do this, we must know how the Laplace transform of is related to the Laplace transform of . The next theorem answers this question.
- Proof
-
We know from Theorem 8.1.6 that is defined for . We first consider the case where is continuous on . Integration by parts yields
for any . Since is of exponential order , and the last integral in (eq:8.3.2) converges as if . Thereforewhich proves (eq:8.3.1). Now suppose and is only piecewise continuous on , with discontinuities at . For convenience, let and . Integrating by parts yieldsSumming both sides of this equation from to and noting that yields (eq:8.3.2), so (eq:8.3.1) follows as before.
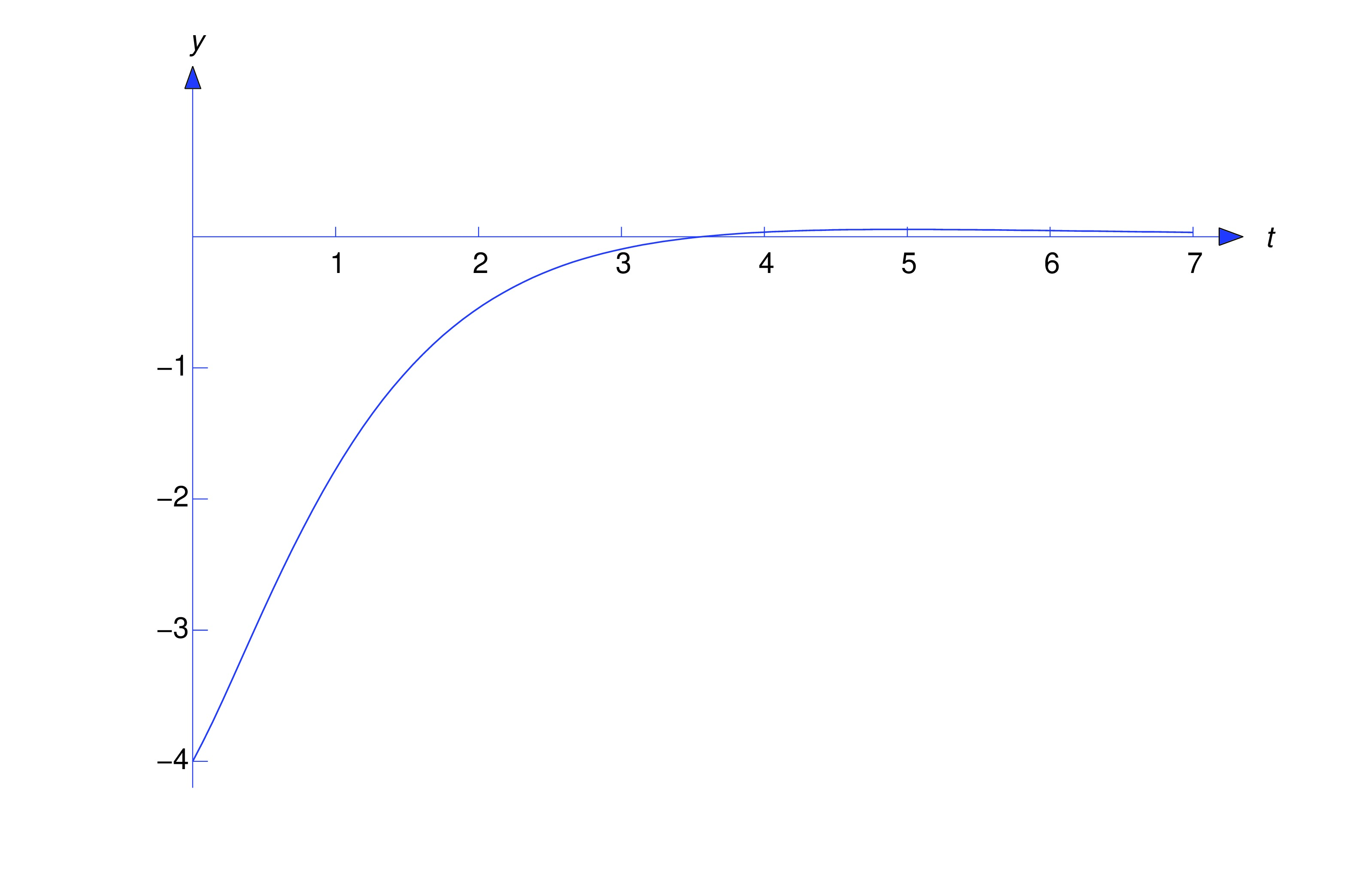
At this point it is easy for us to check (do so!) that the solution of the initial value problem
is . We’ll now obtain this result by using the Laplace transform.Let be the Laplace transform of the unknown solution of (eq:8.3.3). Taking Laplace transforms of both sides of (eq:8.3.3) yields which, by Theorem thmtype:8.3.1, can be rewritten as or Solving for yields so which agrees with the known result.
We need the next theorem to solve second order differential equations using the Laplace transform.
- Proof
- Theorem thmtype:8.3.1 implies that exists and satisfies (eq:8.3.4) for . To prove that exists and satisfies (eq:8.3.5) for , we first apply Theorem thmtype:8.3.1 to . Since satisfies the hypotheses of Theorem thmtype:8.3.1, we conclude that is defined and satisfies for . However, since , this can be rewritten as Substituting (eq:8.3.4) into this yields (eq:8.3.5).
Solving Second Order Equations with the Laplace Transform
We’ll now use the Laplace transform to solve initial value problems for second order equations.
It isn’t necessary to write all the steps that we used to obtain (eq:8.3.8). To see how to avoid this, let’s apply the method of Example example:8.3.2 to the general initial value problem
Taking Laplace transforms of both sides of the differential equation in (eq:8.3.9) yields
Now let . Theorem thmtype:8.3.2 and the initial conditions in (eq:8.3.9) imply that Substituting these into (eq:8.3.10) yields The coefficient of on the left is the characteristic polynomial of the complementary equation for (eq:8.3.9). Using this and moving the terms involving and to the right side of (eq:8.3.11) yields This equation corresponds to (eq:8.3.8) of Example example:8.3.2. Having established the form of this equation in the general case, it is preferable to go directly from the initial value problem to this equation. You may find it easier to remember (eq:8.3.12) rewritten as
Text Source
Trench, William F., ”Elementary Differential Equations” (2013). Faculty Authored and Edited Books & CDs. 8. (CC-BY-NC-SA)