We study the solution of initial value problems where the external force is an impulse.
Constant Coefficient Equations with Impulses
So far in this chapter, we’ve considered initial value problems for the constant coefficient equation where is continuous or piecewise continuous on . In this section we consider initial value problems where represents a force that’s very large for a short time and zero otherwise. We say that such forces are impulsive. Impulsive forces occur, for example, when two objects collide. Since it isn’t feasible to represent such forces as continuous or piecewise continuous functions, we must construct a different mathematical model to deal with them.
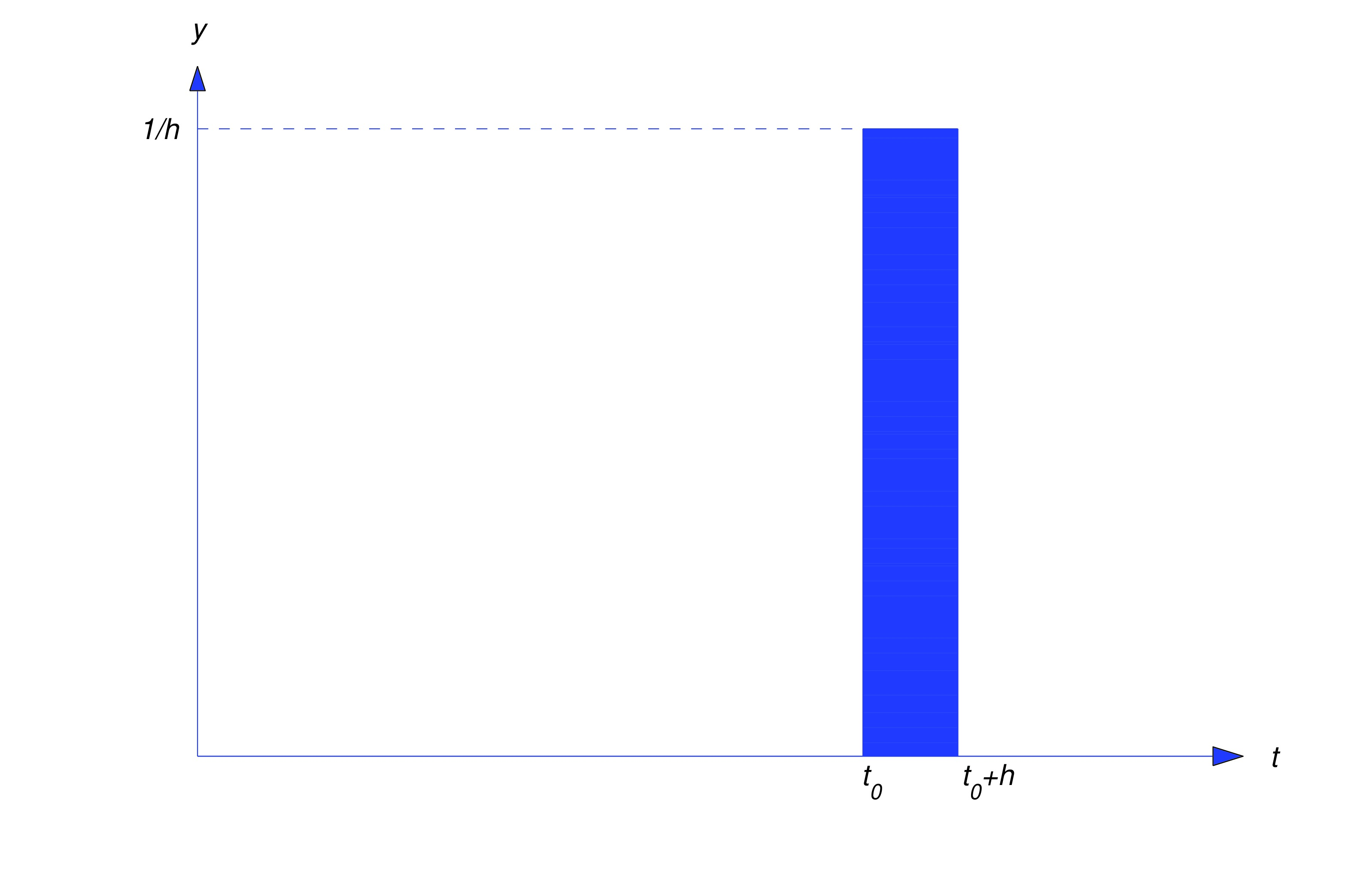
If is an integrable function and for outside of the interval , then is called the total impulse of . We’re interested in the idealized situation where is so small that the total impulse can be assumed to be applied instantaneously at . We say in this case that is an impulse function. In particular, we denote by the impulse function with total impulse equal to one, applied at . (The impulse function obtained by setting is the Dirac function.) It must be understood, however, that isn’t a function in the standard sense, since our “definition” implies that if , while From calculus we know that no function can have these properties; nevertheless, there’s a branch of mathematics known as the theory of distributions where the definition can be made rigorous. Since the theory of distributions is beyond the scope of this book, we’ll take an intuitive approach to impulse functions.
Our first task is to define what we mean by the solution of the initial value problem where is a fixed nonnegative number. The next theorem will motivate our definition.
Then
where
- Proof
- Taking Laplace transforms in (eq:8.7.1) yields
so
The convolution theorem implies that
Therefore, (eq:8.7.2) implies that
Since for all if , it follows that
We’ll now show that
Suppose is fixed and . From (eq:8.7.4),
Since we can write From this and (eq:8.7.7), Therefore Now let be the maximum value of as varies over the interval . (Remember that and are fixed.) Then (eq:8.7.8) and (eq:8.7.9) imply that But , since is continuous. Therefore (eq:8.7.10) implies (eq:8.7.6). This and (eq:8.7.5) imply (eq:8.7.3).
Theorem thmtype:8.7.1 motivates the next definition.
In physical applications where the input and the output of a device are related by the differential equation is called the impulse response of the device. Note that is the solution of the initial value problem
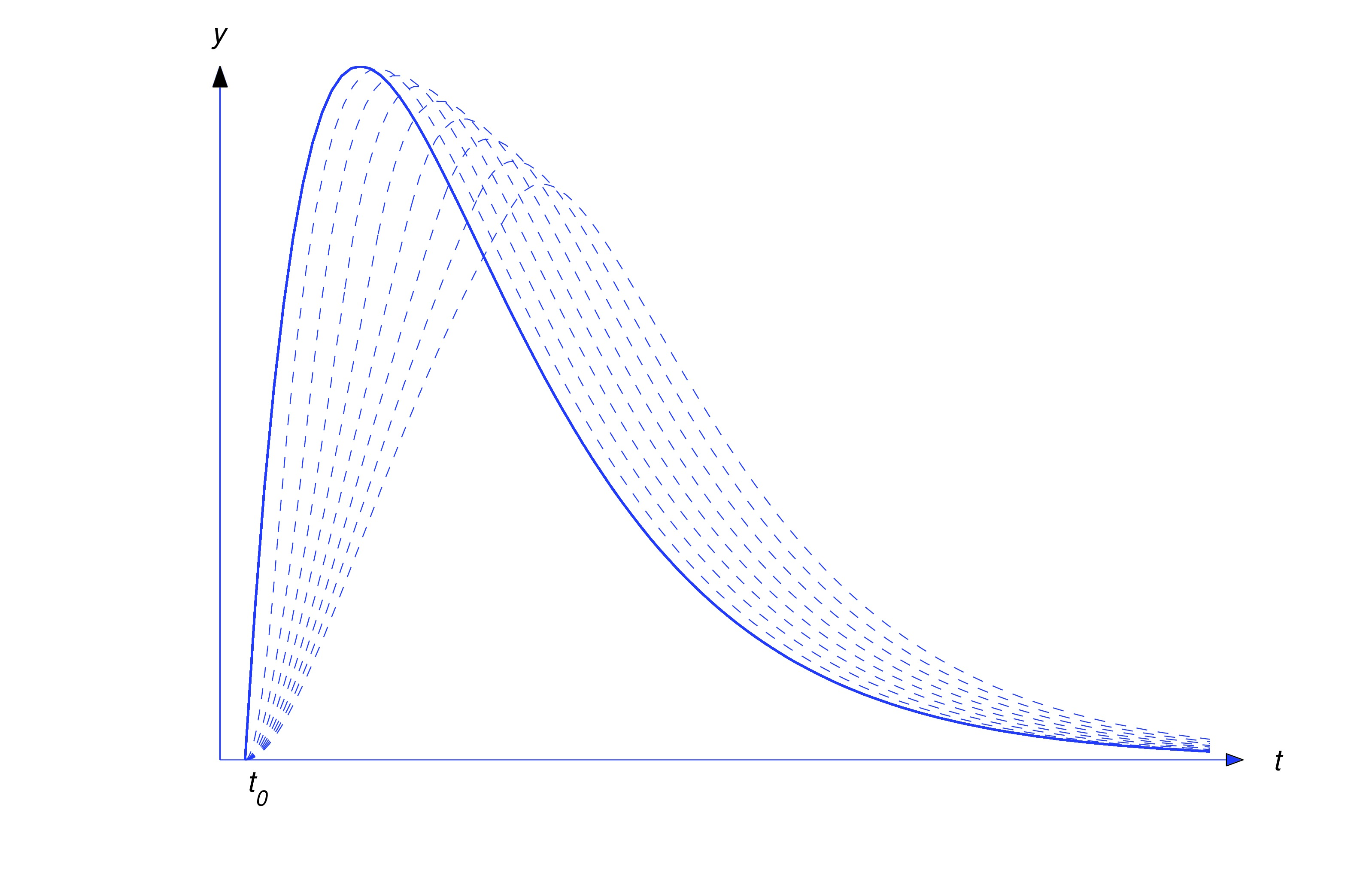
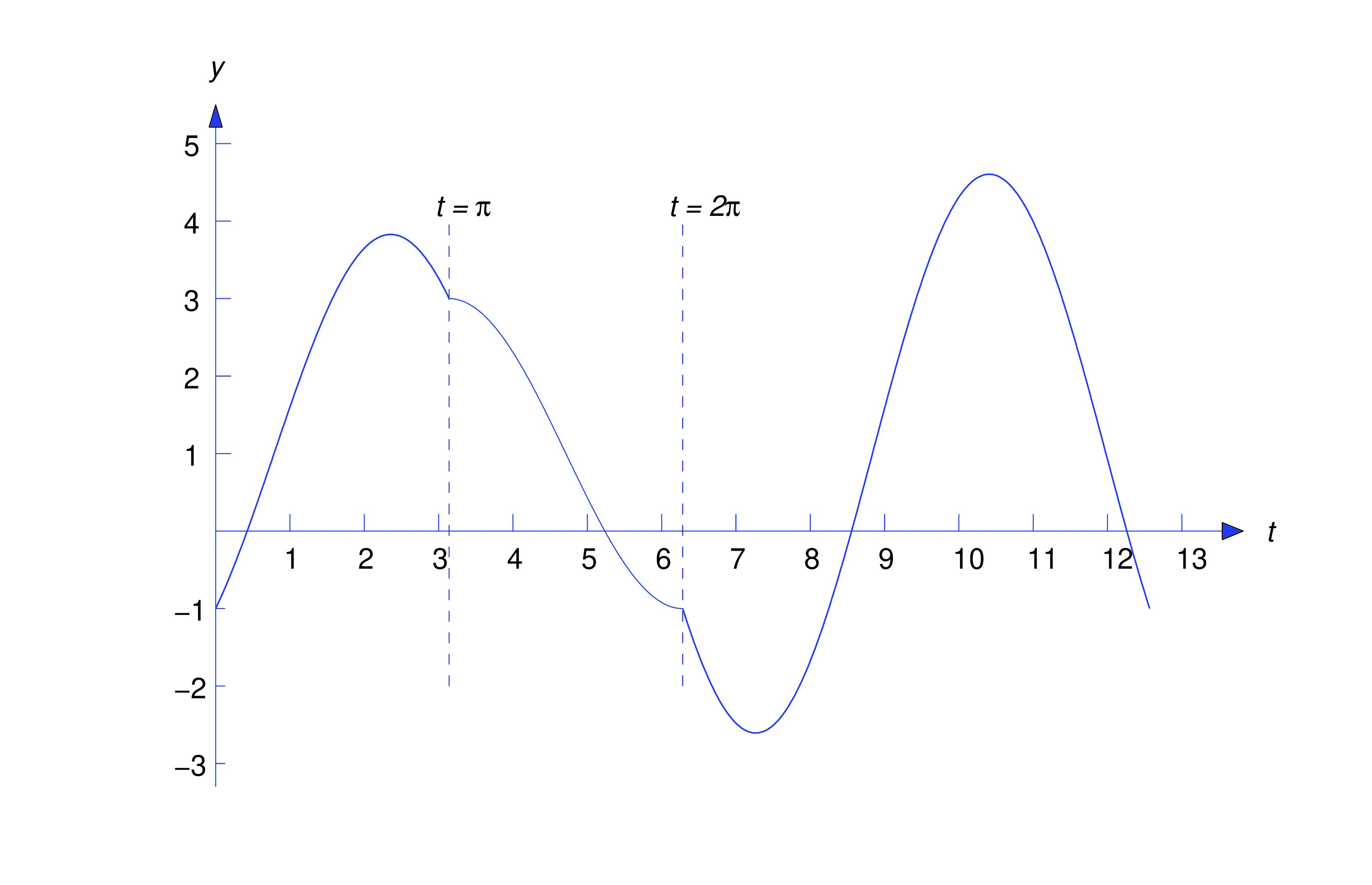
as can be seen by using the Laplace transform to solve this problem. (Verify.) On the other hand, we can solve (eq:8.7.12) by the methods of Trench 5.2 and show that is defined on by depending upon whether the polynomial has distinct real zeros and , a repeated zero , or complex conjugate zeros . (In most physical applications, the zeros of the characteristic polynomial have negative real parts, so .) This means that is defined on and has the following properties: and (remember that and are derivatives from the right and left, respectively) and does not exist. Thus, even though we defined to be the solution of (eq:8.7.11), this function doesn’t satisfy the differential equation in (eq:8.7.11) at , since it isn’t differentiable there; in fact (eq:8.7.14) indicates that an impulse causes a jump discontinuity in velocity. (To see that this is reasonable, think of what happens when you hit a ball with a bat.) This means that the initial value problem (eq:8.7.11) doesn’t make sense if , since doesn’t exist in this case. However can be defined to be the solution of the modified initial value problem where the condition on the derivative at has been replaced by a condition on the derivative from the left.The figure below illustrates Theorem thmtype:8.7.1 for the case where the impulse response is the first expression in (eq:8.7.13) and and are distinct and both negative. The solid curve in the figure is the graph of . The dashed curves are solutions of (eq:8.7.1) for various values of . As decreases the graph of moves to the left toward the graph of .
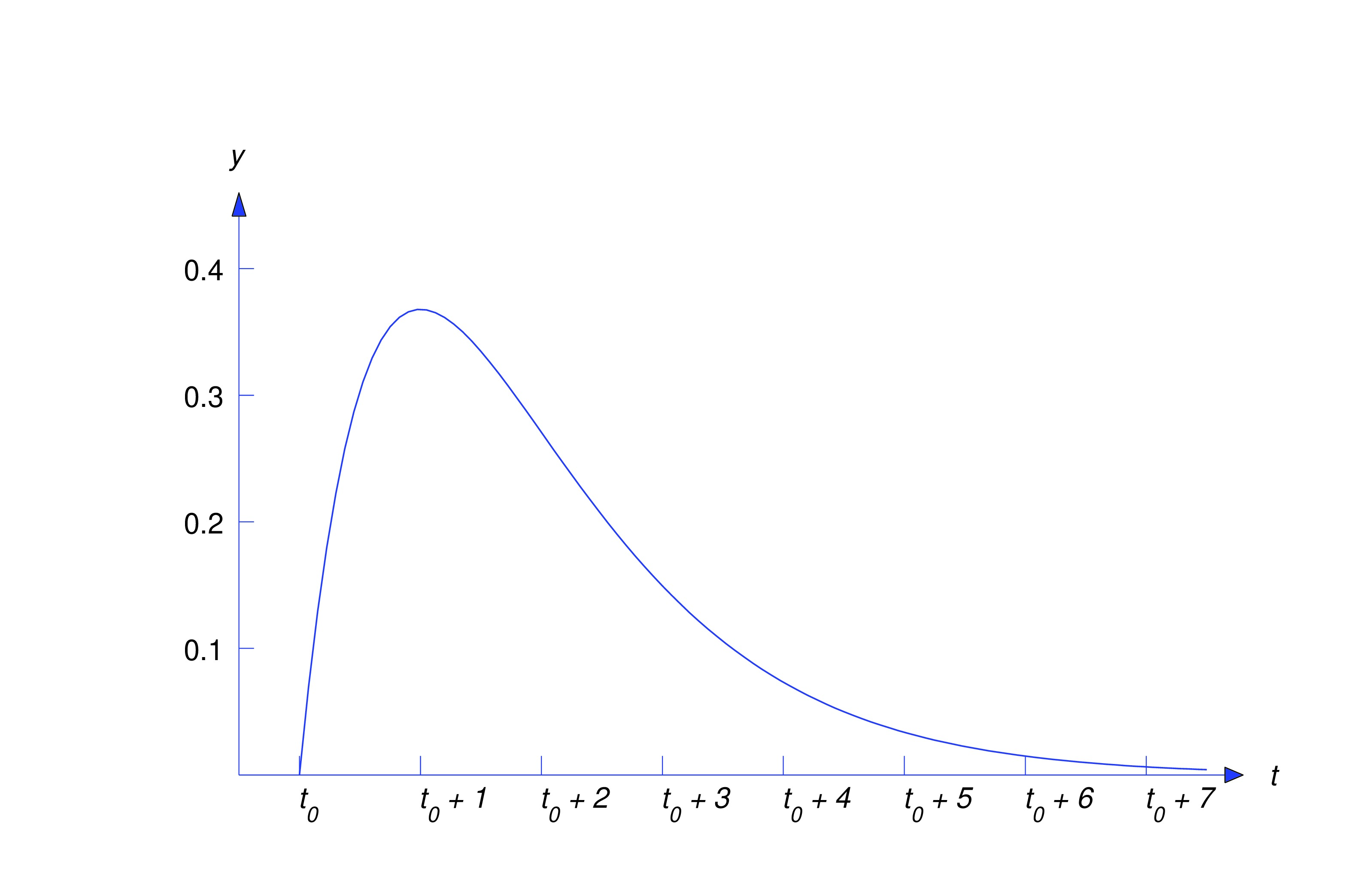
The graph of is shown in the figure below.
Definition thmtype:8.7.2 and the principle of superposition motivate the next definition.
Definition thmtype:8.7.3 can be extended in the obvious way to cover the case where the forcing function contains more than one impulse.
Text Source
Trench, William F., ”Elementary Differential Equations” (2013). Faculty Authored and Edited Books & CDs. 8. (CC-BY-NC-SA)