We show how Laplace Transforms may be used to solve initial value problems with piecewise continuous forcing functions.

Constant Coefficient Equations with Piecewise Continuous Forcing Functions

We’ll now consider initial value problems of the form

where , , and are constants () and is piecewise continuous on . Problems of this kind occur in situations where the input to a physical system undergoes instantaneous changes, as when a switch is turned on or off or the forces acting on the system change abruptly.

It can be shown that the differential equation in (eq:8.5.1) has no solutions on an open interval that contains a jump discontinuity of . Therefore we must define what we mean by a solution of (eq:8.5.1) on in the case where has jump discontinuities. The next theorem motivates our definition. We omit the proof.

We define the function of Theorem thmtype:8.5.1 to be the solution of the initial value problem (eq:8.5.1).

We begin by considering initial value problems of the form

where the forcing function has a single jump discontinuity at .

We can solve (eq:8.5.2) by the these steps:

It can be shown that exists and is continuous at . The next example illustrates this procedure.

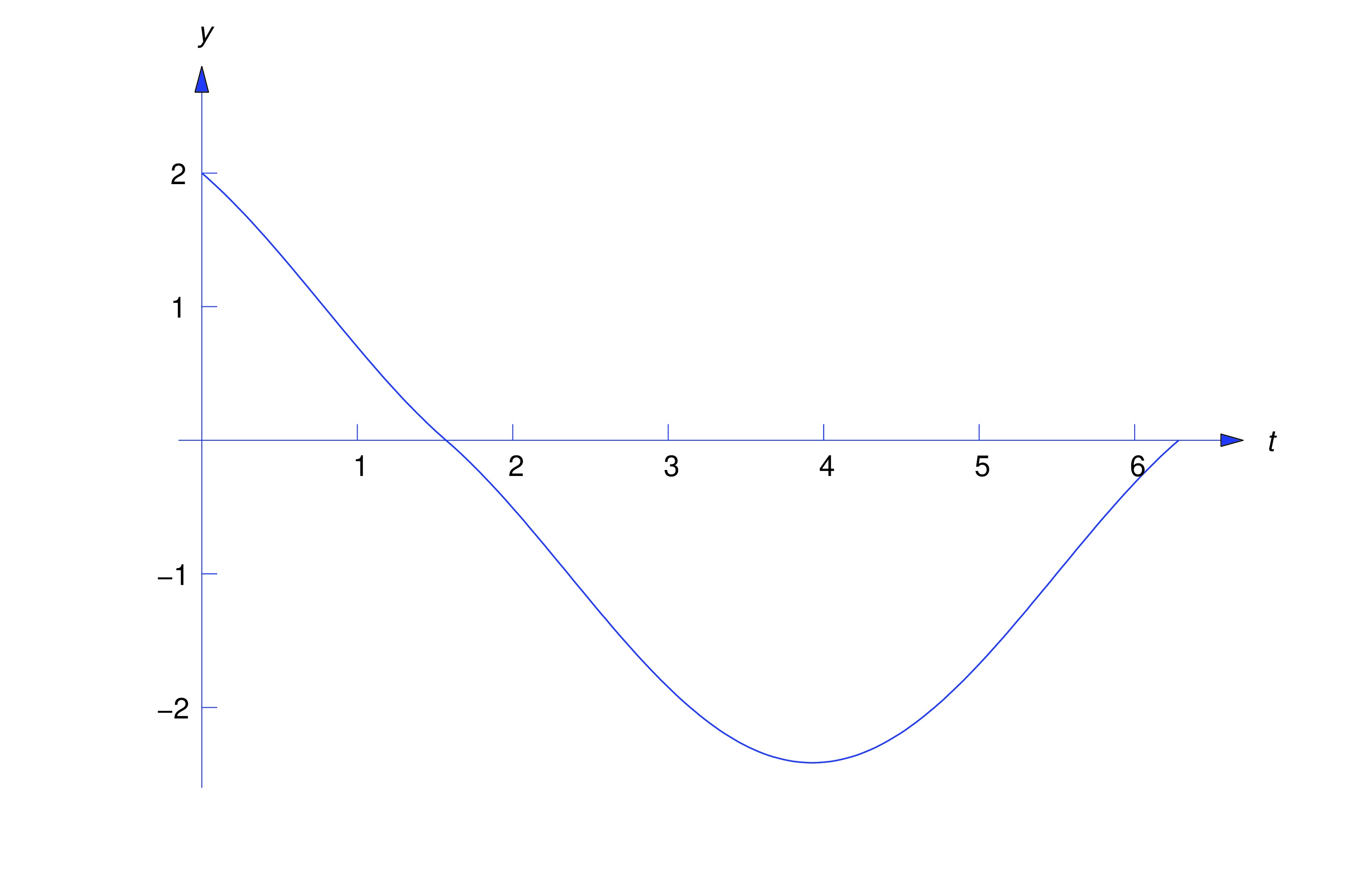
If and are defined on , we can rewrite (eq:8.5.2) as and apply the method of Laplace transforms. We’ll now solve the problem considered in Example example:8.5.1 by this method.

Text Source

Trench, William F., ”Elementary Differential Equations” (2013). Faculty Authored and Edited Books & CDs. 8. (CC-BY-NC-SA)

https://digitalcommons.trinity.edu/mono/8/