The general linear constant coefficient system in two unknown functions is:
The uncoupled systems studied in Section ?? are obtained by setting in (??). We have discussed how to solve (??) by formula (??) when the system is uncoupled. We have also discussed how to visualize the phase plane for different choices of the diagonal entries and . At present, we cannot solve (??) by formula when the coefficient matrix is not diagonal. But we may use pplane5 to solve the initial value problems numerically for these coupled systems. We illustrate this point by solvingEigendirections
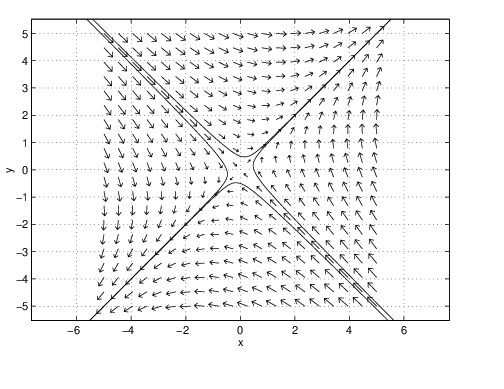
After computing several solutions, we find that for increasing time all the solutions seem to approach the diagonal line given by the equation . Similarly, in backward time the solutions approach the anti-diagonal . In other words, as for the case of uncoupled systems, we find two distinguished directions in the -plane. See Figure ??. Moreover, the computations indicate that these lines are invariant in the sense that solutions starting on these lines remain on them for all time. This statement can be verified numerically by using the Keyboard input in the PPLANE5 Options to choose initial conditions and .
Observe that eigendirections vary if we change parameters. For example, if we set to , then there are still two distinguished lines but these lines are no longer perpendicular.
For uncoupled systems, we have shown analytically that the and axes are eigendirections. The numerical computations that we have just performed indicate that eigendirections exist for many coupled systems. This discussion leads naturally to two questions:
- (a)
- Do eigendirections always exist?
- (b)
- How can we find eigendirections?
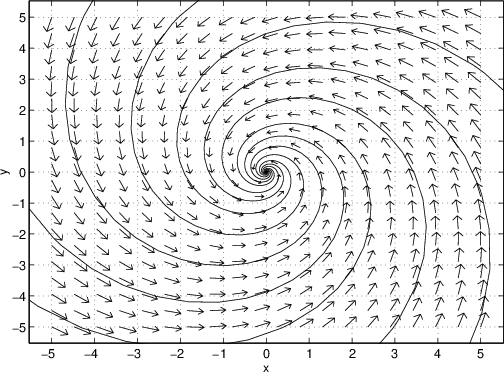
The second question will be answered in Sections ?? and ??. We can answer the first question by performing another numerical computation. In the setup window, change the parameter to . Then numerically compute some solutions to see that there are no eigendirections in the phase space of this system. Observe that all solutions appear to spiral into the origin as time goes to infinity. The phase portrait is shown in Figure ??.
Second Order Differential Equations
We now show analytically that certain linear systems of differential equations have no invariant lines in their phase portrait.
We do this by showing that second order differential equations can be reduced to first order systems by a simple but important trick. Indeed, sometimes it is easier to solve a single second order equation, and sometimes it is easier to solve the first order system. At this stage we introduce this connection by considering the differential equation
This differential equation states that we are looking for a function whose second derivative is . From calculus, we know that is such a function.Let . Then (??) may be rewritten as a first order coupled system in and as follows:
Observe that if is a solution to (??), then Hence, Conversely, if is a solution to (??), then is a solution to (??). That is,It follows from the discussion that is a solution to the differential equation (??). We have shown analytically that the unit circle centered at the origin is a solution trajectory for (??). Hence (??) has no eigendirections. It may be checked using MATLAB that all solution trajectories for (??) are just circles centered at the origin.
Exercises
- spiral into the origin;
- spiral away from the origin;
- form circles around the origin;
- When typical trajectories approach the line as and the line as .
- Assume that is positive, is negative, and . With these assumptions show that the origin is a sink and that typical trajectories approach the origin tangent to the line .
In Exercises ?? – ??, determine which of the function pairs and are solutions to the given system of ordinary differential equations.