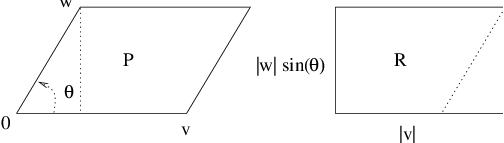The Geometry of Vector Operations

$\newenvironment {prompt}{}{} \newcommand {\Sec }[2]{\section {#1}} \newcommand {\trademark }[0]{{R\!\!\!\!\!\bigcirc }} \newcommand {\EXER }[0]{\section *{Exercises}} \newcommand {\CEXER }[0]{} \newcommand {\TEXER }[0]{} \newcommand {\R }[0]{\mbox {$\Bbb {R}$}} \newcommand {\C }[0]{\mbox {$\Bbb {C}$}} \newcommand {\Z }[0]{\mbox {$\Bbb {Z}$}} \newcommand {\N }[0]{\mbox {$\Bbb {N}$}} \newcommand {\D }[0]{\mbox {{\bf D}}} \newcommand {\setmin }[0]{\;\mbox {--}\;} \newcommand {\Matlab }[0]{{M\small {AT\-LAB}} } \newcommand {\Matlabp }[0]{{M\small {AT\-LAB}}} \newcommand {\computer }[0]{\Matlab Instructions} \newcommand {\half }[0]{\mbox {$\frac {1}{2}$}} \newcommand {\compose }[0]{\raisebox {.15ex}{\mbox {{\scriptsize $\circ $}}}} \newcommand {\AND }[0]{\quad \mbox {and}\quad } \newcommand {\vect }[2]{\left (\begin {array}{c} #1_1 \\ \vdots \\ #1_{#2}\end {array}\right )} \newcommand {\mattwo }[4]{\left (\begin {array}{rr} #1 & #2\\ #3 &#4\end {array}\right )} \newcommand {\mattwoc }[4]{\left (\begin {array}{cc} #1 & #2\\ #3 &#4\end {array}\right )} \newcommand {\vectwo }[2]{\left (\begin {array}{r} #1 \\ #2\end {array}\right )} \newcommand {\vectwoc }[2]{\left (\begin {array}{c} #1 \\ #2\end {array}\right )} \newcommand {\inv }[0]{^{-1}} \newcommand {\CC }[0]{{\cal C}} \newcommand {\CCone }[0]{\CC ^1} \newcommand {\Span }[0]{{\rm span}} \newcommand {\rank }[0]{{\rm rank}} \newcommand {\trace }[0]{{\rm tr}} \newcommand {\RE }[0]{{\rm Re}} \newcommand {\IM }[0]{{\rm Im}} \newcommand {\nulls }[0]{{\rm null\;space}} \newcommand {\dps }[0]{\displaystyle } \newcommand {\arraystart }[0]{\renewcommand {\arraystretch }{1.8}} \newcommand {\arrayfinish }[0]{\renewcommand {\arraystretch }{1.2}} \newcommand {\Start }[1]{\vspace {0.08in}\noindent {\bf Section~\ref {#1}}} \newcommand {\exer }[1]{\noindent {\bf \ref {#1}}} \newcommand {\ans }[0]{} \newcommand {\matthree }[9]{\left (\begin {array}{rrr} #1 & #2 & #3 \\ #4 & #5 & #6 \\ #7 & #8 & #9\end {array}\right )} \newcommand {\cvectwo }[2]{\left (\begin {array}{c} #1 \\ #2\end {array}\right )} \newcommand {\cmatthree }[9]{\left (\begin {array}{ccc} #1 & #2 & #3 \\ #4 & #5 & #6 \\ #7 & #8 & #9\end {array}\right )} \newcommand {\vecthree }[3]{\left (\begin {array}{r} #1 \\ #2 \\ #3\end {array}\right )} \newcommand {\cvecthree }[3]{\left (\begin {array}{c} #1 \\ #2 \\ #3\end {array}\right )} \newcommand {\cmattwo }[4]{\left (\begin {array}{cc} #1 & #2\\ #3 &#4\end {array}\right )} \newcommand {\thehelp }[0]{\thesection .\arabic {equation}} \newcommand {\matlabEquation }[0]{\let \oldtheequation \theequation \renewcommand {\theequation }{\oldtheequation *}\begin {equation}} \newcommand {\HyperFirstAtBeginDocument }[0]{\AtBeginDocument } \newcommand {\epstopdfsetup }[0]{\setkeys {ETE}} changed the theorem header of amsthm failed\MessageBreak }}} \newcommand {\GetTitleStringSetup }[0]{\setkeys {gettitlestring}} \newcommand {\Sectionformat }[2]{#1}$ $% This file was *autogenerated* from theGeometryOfVectorOperations.sagetex.sage with % sagetex.py version 2015/08/26 v3.0-92d9f7a %6c9e17e6703d69eae41d34c60215acff% md5sum of corresponding .sage file (minus "goboom","current_tex_line",and pause/unpause lines)$

In this section we discuss the geometry of addition, scalar multiplication, and dot product of vectors. We also use MATLAB graphics to visualize these operations.

Geometry of Addition

MATLAB has an excellent graphics language that we shall use at various times to illustrate concepts in both two and three dimensions. In order to make the connections between ideas and graphics more transparent, we will sometimes use previously developed MATLAB programs. We begin with such an example — the illustration of the parallelogram law for vector addition.

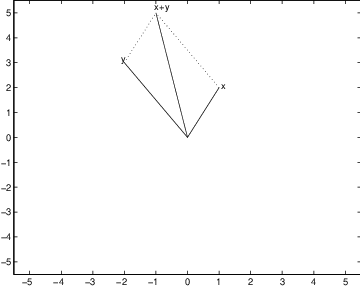
Suppose that $x$ and $y$ are two planar vectors. Think of these vectors as line segments from the origin to the points $x$ and $y$ in $\R ^2$ . We use a program written by T.A. Bryan to visualize $x+y$ . In MATLAB type¹ :

x = [1 2];
 
y = [-2 3];
 
addvec(x,y)

The vector $x$ is displayed in blue, the vector $y$ in green, and the vector $x+y$ in red. Note that $x+y$ is just the diagonal of the parallelogram spanned by $x$ and $y$ . A black and white version of this figure is given in Figure ??.

Figure 1: Addition of two planar vectors.

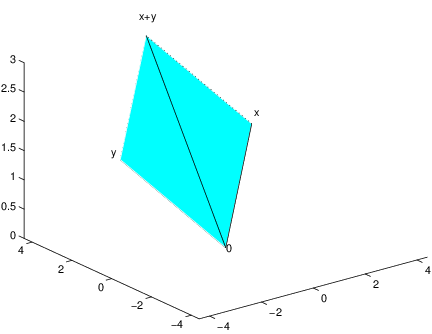
The parallelogram law (the diagonal of the parallelogram spanned by $x$ and $y$ is $x+y$ ) is equally valid in three dimensions. Use MATLAB to verify this statement by typing:

x = [1 0 2];
 
y = [-1 4 1];
 
addvec3(x,y)

The parallelogram spanned by $x$ and $y$ in $\R ^3$ is shown in cyan; the diagonal $x+y$ is shown in blue. See Figure ??. To test your geometric intuition, make several choices of vectors $x$ and $y$ . Note that one vertex of the parallelogram is always the origin.

Figure 2: Addition of two vectors in three dimensions.

Geometry of Scalar Multiplication

In all dimensions scalar multiplication just scales the length of the vector. To discuss this point we need to define the length of a vector. View an $n$ -vector $x=(x_1,\ldots ,x_n)$ as a line segment from the origin to the point $x$ . Using the Pythagorean theorem, it can be shown that the length or norm of this line segment is: $||x|| = \sqrt {x_1^2 + \cdots + x_n^2}.$ MATLAB has the command norm for finding the length of a vector. Test this by entering the $3$ -vector

x = [1 4 2];

Then type

norm(x)

MATLAB responds with:

ans =
 
    4.5826

which is indeed approximately $\sqrt {1+4^2+2^2} = \sqrt {21}$ .

Now suppose $r\in \R$ and $x\in \R ^n$ . A calculation shows that

$\begin{equation} \label{E:lengths} ||rx|| = |r| ||x||. \end{equation}$ See Exercise ??. Note also that if $r$ is positive, then the direction of $rx$ is the same as that of $x$ ; while if $r$ is negative, then the direction of $rx$ is opposite to the direction of $x$ . The lengths of the vectors $3x$ and $-3x$ are each three times the length of $x$ — but these vectors point in opposite directions. Scalar multiplication by the scalar $0$ produces the $0$ vector, the vector whose entries are all zero.

Dot Product and Angles

The dot product of two $n$ -vectors $x=(x_1,\ldots ,x_n)$ and $y=(y_1,\ldots ,y_n)$ is an important operation on vectors. It is defined by:

$\begin{equation} \label{e:dotproduct} x\cdot y = x_1y_1 + \cdots + x_ny_n. \end{equation}$ Note that $x\cdot x$ is just $||x||^2$ , the length of $x$ squared.

MATLAB also has a command for computing dot products of $n$ -vectors. Type

x = [1 4 2];
 
y = [2 3 -1];
 
dot(x,y)

MATLAB responds with the dot product of $x$ and $y$ , namely,

ans =
 
    12

One of the most important facts concerning dot products is the one that states

$\begin{equation} \label{dotprod=0} x\cdot y = 0 \quad \mbox{if and only if} \quad \mbox{$x$ and $y$ are perpendicular}. \end{equation}$ Indeed, dot product also gives a way of numerically determining the angle between $n$ -vectors, as follows.

Let $\theta$ be the angle between two nonzero $n$ -vectors $x$ and $y$ . Then $\begin{equation} \label{e:dotproductang} \cos \theta = \frac{x\cdot y}{||x|| ||y||}. \end{equation}$

It follows that $\cos \theta =0$ if and only if $x\cdot y = 0$ . Thus (??) is valid.

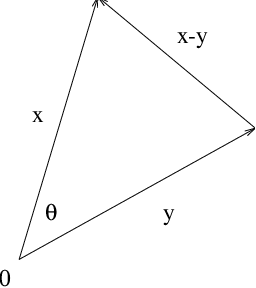
Proof: Theorem ?? is just a restatement of the law of cosines. Recall that the law of cosines states that $c^2 = a^2 + b^2 -2ab\cos \theta ,$ where $a,b,c$ are the lengths of the sides of a triangle and $\theta$ is the interior angle opposite the side of length $c$ . In vector notation we can form a triangle two of whose sides are given by $x$ and $y$ in $\R ^n$ . The third side is just $x-y$ as $x=y+(x-y)$ , as in Figure ??.

Figure 3: Triangle formed by vectors $x$ and $y$ with interior angle $\theta$ .

It follows from the law of cosines that $||x-y||^2 = ||x||^2 + ||y||^2 - 2||x|| ||y|| \cos \theta .$ We claim that $||x-y||^2 = ||x||^2 + ||y||^2 -2x\cdot y.$ Assuming that the claim is valid, it follows that $x\cdot y = ||x|| ||y|| \cos \theta ,$ which proves the theorem. Finally, compute
$\begin{eqnarray*} ||x-y||^2 & = &(x_1-y_1)^2 + \cdots + (x_n-y_n)^2 \\ & = & (x_1^2-2x_1y_1+y_1^2) + \cdots + (x_n^2-2x_ny_n+y_n^2)\\ & = & (x_1^2+\cdots+x_n^2)-2(x_1y_1+\cdots+x_ny_n)+(y_1^2+\cdots+y_n^2)\\ & = & ||x||^2 -2x\cdot y + ||y||^2 \end{eqnarray*}$
to verify the claim. $\blacksquare$

Theorem ?? gives a numerically efficient method for computing the angle between vectors $x$ and $y$ . In MATLAB this computation proceeds by typing

theta = acos(dot(x,y)/(norm(x)*norm(y)))

where acos is the inverse cosine of a number. For example, using the $3$ -vectors $x = (1,4,2)$ and $y = (2,3,-1)$ entered previously, MATLAB responds with

theta =
 
    0.7956

Remember that this answer is in radians. To convert this answer to degrees, just multiply by $360$ and divide by $2\pi$ :

360*theta / (2*pi)

to obtain the answer of $45.5847^\circ$ .

Area of Parallelograms

Let $P$ be a parallelogram whose sides are the vectors $v$ and $w$ as in Figure ??. Let $|P|$ denote the area of $P$ . As an application of dot products and (??), we calculate $|P|$ . We claim that

$\begin{equation} \label{e:areaP} |P|^2 = ||v||^2||w||^2 - (v\cdot w)^2. \end{equation}$ We verify (??) as follows. Note that the area of $P$ is the same as the area of the rectangle $R$ also pictured in Figure ??. The side lengths of $R$ are: $||v||$ and $||w||\sin \theta$ where $\theta$ is the angle between $v$ and $w$ . A computation using (??) shows that

$\begin{eqnarray*} |R|^2 & = & ||v||^2 ||w||^2\sin^2\theta \\ & = & ||v||^2 ||w||^2(1-\cos^2\theta) \\ & = & ||v||^2 ||w||^2\left(1-\left(\frac{v\cdot w}{||v|| ||w||} \right)^2\right)\\ & = & ||v||^2 ||w||^2 - (v\cdot w)^2, \end{eqnarray*}$

which establishes (??).

Figure 4: Parallelogram $P$ beside rectangle $R$ with same area.

Exercises

In Exercises ?? – ?? compute the lengths of the given vectors.

$x=(3,0)$ . The length of $x$ is $\answer {3}$ .

$x=(2,-1)$ . The length of $x$ is $\answer {\sqrt {5}}$ .

$x=(-1,1,1)$ . The length of $x$ is $\answer {\sqrt {3}}$ .

$x=(-1,0,2,-1,3)$ . The length of $x$ is $\answer {15}$ .

In Exercises ?? – ?? determine whether the given pair of vectors is perpendicular.

$x=(1,3)$ and $y=(3,-1)$ .

The vectors are perpendicular. The vectors are not perpendicular.

Vectors $x$ and $y$ are perpendicular if and only if $x \cdot y = 0$ . In this case, $(1,3) \cdot (3,-1) = 0$ .

$x=(2,-1)$ and $y=(-2,1)$ .

The vectors are perpendicular. The vectors are not perpendicular.

Compute: $(2,-1) \cdot (-2,1) = -5$ .

$x=(1,1,3,5)$ and $y=(1,-4,3,0)$ .

The vectors are perpendicular. The vectors are not perpendicular.

Compute: $(1,1,3,5) \cdot (1,-4,3,0) = 6$ .

$x=(2,1,4,5)$ and $y=(1,-4,3,-2)$ .

The vectors are perpendicular. The vectors are not perpendicular.

Compute: $(2,1,4,5) \cdot (1,-4,3,-2) = 0$ .

Find a real number $a\begin {prompt}=\answer {10/3}\end {prompt}$ so that the vectors $x = (1,3,2) \AND y = (2,a,-6)$ are perpendicular.

The vectors $x$ and $y$ are perpendicular when $(1,3,2) \cdot (2,a,-6) = 3a - 10 = 0$ .

This means that $a = \frac {10}{3}$ .

Find the lengths of the vectors $u=(2,1,-2)$ and $v=(0,1,-1)$ , and the angle $\theta = \answer {\pi /4}$ in radians between them. $||u|| = \answer {3} \mbox { and } ||v|| = \answer {\sqrt {2}}$

$||u|| = \sqrt {2^2 + 1^2 + (-2)^2}$ .

$||v|| = \sqrt {0^2 + 1^2 + (-1)^2}$ .

$\cos \theta = \frac {u \cdot v}{||u||\;||v||} = \frac {3}{3\sqrt {2}} = \frac {1}{\sqrt {2}}$

So $\theta = \frac {\pi }{4}$ .

In Exercises ?? – ?? compute the dot product $x\cdot y$ for the given pair of vectors and the cosine of the angle $\theta$ in radians between them.

$x=(2,0)$ and $y=(2,1)$ . $x \cdot y = \answer {4} \mbox { and } \cos \theta = \answer {\frac {2}{\sqrt {5}}}$

$x=(2,-1)$ and $y=(1,2)$ . $x \cdot y = \answer {0} \mbox { and } \cos \theta = \answer {0}$

$x=(-1,1,4)$ and $y=(0,1,3)$ . $x \cdot y = \answer {13} \mbox { and } \cos \theta = \answer {\frac {13}{6\sqrt {5}}}$

$x=(-10,1,0)$ and $y=(0,1,20)$ . $x \cdot y = \answer {1} \mbox { and } \cos \theta = \answer {\frac {1}{\sqrt {40501}}}$

$x=(2,-1,1,3,0)$ and $y=(4,0,2,7,5)$ . $x \cdot y = \answer {31} \mbox { and } \cos \theta = \answer {\frac {31}{\sqrt {1410}}}$

$x=(5,-1,4,1,0,0)$ and $y=(-3,0,0,1,10,-5)$ . $x \cdot y = \answer {-14} \mbox { and } \cos \theta = \answer {\frac {-14}{\sqrt {5805}}}$

Using the definition of length, verify that formula (??) is valid. $\begin{align*} ||rx|| & = ||\answer{r}(x_1,\dots,x_n)|| \\ & = ||(\answer{r}x_1,\dots,\answer{r}x_n)|| \\ & = \sqrt{(rx_1)^2 + \cdots + (rx_n)^2} \\ & = \sqrt{ \answer{r^2} (x_1^2 + \cdots + x_n^2)} \\ & = |\answer{r}|\sqrt{x_1^2 + \cdots + x_n^2} \\ & = |\answer{r}| ||x||. \end{align*}$

Use addvec and addvec3 to add vectors in $\R ^2$ and $\R ^3$ . More precisely, enter pairs of $2$ -vectors x and y of your choosing into MATLAB, use addvec to compute x+y, and note the parallelogram formed by $0,x,y,x+y$ . Similarly, enter pairs of $3$ -vectors and use addvec3.

Determine the vector of length $1$ that points in the same direction as the vector $x=(2,13.5,-6.7,5.23).$

Determine the vector of length $1$ that points in the same direction as the vector $y=(2.1,-3.5,1.5,1.3,5.2).$

In Exercises ??– ?? find the angle in degrees between the given pair of vectors.

$x=(2,1,-3,4)$ and $y=(1,1,-5,7)$ .

$x=(2.43, 10.2,-5.27,\pi )$ and $y= (-2.2,0.33,4,-1.7)$ .

$x=(1,-2,2,1,2.1)$ and $y=(-3.44,1.2,1.5,-2,-3.5)$ .

In Exercises ?? – ?? let $P$ be the parallelogram generated by the given vectors $v$ and $w$ in $\R ^3$ . Compute the area of that parallelogram.

$v=(1,5,7)$ and $w=(-2,4,13)$ .

$v=(2,-1,1)$ and $w=(-1,4,3)$ .