Determinants

$\newenvironment {prompt}{}{} \newcommand {\Sec }[2]{\section {#1}} \newcommand {\trademark }[0]{{R\!\!\!\!\!\bigcirc }} \newcommand {\EXER }[0]{\section *{Exercises}} \newcommand {\CEXER }[0]{} \newcommand {\TEXER }[0]{} \newcommand {\R }[0]{\mbox {$\Bbb {R}$}} \newcommand {\C }[0]{\mbox {$\Bbb {C}$}} \newcommand {\Z }[0]{\mbox {$\Bbb {Z}$}} \newcommand {\N }[0]{\mbox {$\Bbb {N}$}} \newcommand {\D }[0]{\mbox {{\bf D}}} \newcommand {\setmin }[0]{\;\mbox {--}\;} \newcommand {\Matlab }[0]{{M\small {AT\-LAB}} } \newcommand {\Matlabp }[0]{{M\small {AT\-LAB}}} \newcommand {\computer }[0]{\Matlab Instructions} \newcommand {\half }[0]{\mbox {$\frac {1}{2}$}} \newcommand {\compose }[0]{\raisebox {.15ex}{\mbox {{\scriptsize $\circ $}}}} \newcommand {\AND }[0]{\quad \mbox {and}\quad } \newcommand {\vect }[2]{\left (\begin {array}{c} #1_1 \\ \vdots \\ #1_{#2}\end {array}\right )} \newcommand {\mattwo }[4]{\left (\begin {array}{rr} #1 & #2\\ #3 &#4\end {array}\right )} \newcommand {\mattwoc }[4]{\left (\begin {array}{cc} #1 & #2\\ #3 &#4\end {array}\right )} \newcommand {\vectwo }[2]{\left (\begin {array}{r} #1 \\ #2\end {array}\right )} \newcommand {\vectwoc }[2]{\left (\begin {array}{c} #1 \\ #2\end {array}\right )} \newcommand {\inv }[0]{^{-1}} \newcommand {\CC }[0]{{\cal C}} \newcommand {\CCone }[0]{\CC ^1} \newcommand {\Span }[0]{{\rm span}} \newcommand {\rank }[0]{{\rm rank}} \newcommand {\trace }[0]{{\rm tr}} \newcommand {\RE }[0]{{\rm Re}} \newcommand {\IM }[0]{{\rm Im}} \newcommand {\nulls }[0]{{\rm null\;space}} \newcommand {\dps }[0]{\displaystyle } \newcommand {\arraystart }[0]{\renewcommand {\arraystretch }{1.8}} \newcommand {\arrayfinish }[0]{\renewcommand {\arraystretch }{1.2}} \newcommand {\Start }[1]{\vspace {0.08in}\noindent {\bf Section~\ref {#1}}} \newcommand {\exer }[1]{\noindent {\bf \ref {#1}}} \newcommand {\ans }[0]{} \newcommand {\matthree }[9]{\left (\begin {array}{rrr} #1 & #2 & #3 \\ #4 & #5 & #6 \\ #7 & #8 & #9\end {array}\right )} \newcommand {\cvectwo }[2]{\left (\begin {array}{c} #1 \\ #2\end {array}\right )} \newcommand {\cmatthree }[9]{\left (\begin {array}{ccc} #1 & #2 & #3 \\ #4 & #5 & #6 \\ #7 & #8 & #9\end {array}\right )} \newcommand {\vecthree }[3]{\left (\begin {array}{r} #1 \\ #2 \\ #3\end {array}\right )} \newcommand {\cvecthree }[3]{\left (\begin {array}{c} #1 \\ #2 \\ #3\end {array}\right )} \newcommand {\cmattwo }[4]{\left (\begin {array}{cc} #1 & #2\\ #3 &#4\end {array}\right )} \newcommand {\thehelp }[0]{\thesection .\arabic {equation}} \newcommand {\matlabEquation }[0]{\let \oldtheequation \theequation \renewcommand {\theequation }{\oldtheequation *}\begin {equation}} \newcommand {\HyperFirstAtBeginDocument }[0]{\AtBeginDocument } \newcommand {\epstopdfsetup }[0]{\setkeys {ETE}} changed the theorem header of amsthm failed\MessageBreak }}} \newcommand {\GetTitleStringSetup }[0]{\setkeys {gettitlestring}} \newcommand {\Sectionformat }[2]{#1} \newcommand {\theequation }[0]{\oldtheequation *} \newcommand {\theequation }[0]{\oldtheequation *}$ $% This file was *autogenerated* from determinants.sagetex.sage with % sagetex.py version 2015/08/26 v3.0-92d9f7a %399b4ee564175961a5f823e13d9a17da% md5sum of corresponding .sage file (minus "goboom","current_tex_line",and pause/unpause lines)$

There are several equivalent ways to introduce determinants — none of which are easily motivated. We prefer to define determinants through the properties they satisfy rather than by formula. These properties actually enable us to compute determinants of $n\times n$ matrices where $n>3$ , which further justifies the approach. Later on, we will give an inductive formula (??) for computing the determinant.

A determinant of a square $n\times n$ matrix $A$ is a real number that satisfies the following three properties:

If $A=(a_{ij})$ is lower triangular, then the determinant of $A$ is the product of the diagonal entries; that is, $\det (A) = a_{11}\cdot \cdots \cdot a_{nn}.$
$\det (A^t)=\det (A)$ .
Let $B$ be an $n\times n$ matrix. Then $\begin{equation} \label{e:detproduct} \det(AB) = \det(A)\det(B). \end{equation}$

There exists a unique determinant function satisfying the three properties of Definition ??.

We will show that it is possible to compute the determinant of any $n\times n$ matrix using Definition ??. Here we present a few examples:

Let $A$ be an $n\times n$ matrix.

Let $c\in \R$ be a scalar. Then $\det (cA) = c^n\det (A)$ .
If all of the entries in either a row or a column of $A$ are zero, then $\det (A)=0$ .

Proof: (a) Note that Definition ??(a) implies that $\det (cI_n)=c^n$ . It follows from (??) that $\det (cA) = \det (cI_n A) = \det (cI_n)\det (A) = c^n\det (A).$
(b) Definition ??(b) implies that it suffices to prove this assertion when one row of $A$ is zero. Suppose that the $i^{th}$ row of $A$ is zero. Let $J$ be an $n\times n$ diagonal matrix with a $1$ in every diagonal entry except the $i^{th}$ diagonal entry which is $0$ . A matrix calculation shows that $JA=A$ . It follows from Definition ??(a) that $\det (J)=0$ and from (??) that $\det (A)=0$ . $\blacksquare$

Determinants of $2\times 2$ Matrices

Before discussing how to compute determinants, we discuss the special case of $2\times 2$ matrices. Recall from (??) of Section ?? that when $A=\left (\begin {array}{cc} a & b\\c & d \end {array}\right )$ we defined

$\begin{equation} \label{e:determinantn=2} \det(A)=ad-bc. \end{equation}$ We check that (??) satisfies the three properties in Definition ??. Observe that when $A$ is lower triangular, then $b=0$ and $\det (A)=ad$ . So (a) is satisfied. It is straightforward to verify (b). We already verified (c) in Chapter ??, Proposition ??.

It is less obvious perhaps — but true nonetheless — that the three properties of $\det (A)$ actually force the determinant of $2\times 2$ matrices to be given by formula (??). We begin by showing that Definition ?? implies that

$\begin{equation} \label{e:detswap} \det \left(\begin{array}{cc} 0 & 1\\1 & 0 \end{array}\right)=-1. \end{equation}$ We verify this by observing that $\begin{equation} \label{MATLAB:41} \left(\begin{array}{cc} 0 & 1\\1 & 0 \end{array}\right) \end{matlabEquation} equals \begin{equation}\label{e:swapdecomp} \left(\begin{array}{cr} 1 & -1\\0 & 1 \end{array}\right) \left(\begin{array}{cc} 1 & 0\\1 & 1 \end{array}\right) \left(\begin{array}{cr} 1 & 0\\0 & -1 \end{array}\right) \left(\begin{array}{cc} 1 & 1\\0 & 1 \end{array}\right). \end{equation}$ Hence property (c), (a) and (b) imply that $\det \left (\begin {array}{cc} 0 & 1\\1 & 0 \end {array}\right ) = 1\cdot 1\cdot (-1) \cdot 1 = -1.$ It is helpful to interpret the matrices in (??) as elementary row operations. Then (??) states that swapping two rows in a $2\times 2$ matrix is the same as performing the following row operations in order:

add the $2^{nd}$ row to the $1^{st}$ row;
multiply the $2^{nd}$ row by $-1$ ;
add the $1^{st}$ row to the $2^{nd}$ row; and
subtract the $2^{nd}$ row from the $1^{st}$ row.

Suppose that $d\neq 0$ . Then $A=\left (\begin {array}{cc} a & b\\c & d \end {array}\right ) = \left (\begin {array}{cc} 1 & \frac {b}{d}\\0 & 1 \end {array}\right ) \left (\begin {array}{cc} \frac {ad-bc}{d} & 0\\c & d \end {array}\right ).$ It follows from properties (c), (b) and (a) that $\det (A) = \frac {ad-bc}{d}d = ad-bc,$ as claimed.

Now suppose that $d=0$ and note that $A=\left (\begin {array}{cc} a & b\\c & 0 \end {array}\right ) = \left (\begin {array}{cc} 0 & 1\\1 & 0 \end {array}\right ) \left (\begin {array}{cc} c & 0\\a & b \end {array}\right ).$ Using (??) we see that $\det (A) = -\det \left (\begin {array}{cc} c & 0\\a & b \end {array}\right ) = -bc,$ as desired.

We have verified that the only possible determinant function for $2\times 2$ matrices is the determinant function defined by (??).

Row Operations are Invertible Matrices

Let $A$ and $B$ be $m\times n$ matrices where $B$ is obtained from $A$ by a single elementary row operation. Then there exists an invertible $m\times m$ matrix $R$ such that $B=RA$ .

Proof

First consider multiplying the $j^{th}$ row of $A$ by the nonzero constant $c$ . Let $R$ be the diagonal matrix whose $j^{th}$ entry on the diagonal is $c$ and whose other diagonal entries are $1$ . Then the matrix $RA$ is just the matrix obtained from $A$ by multiplying the $j^{th}$ row of $A$ by $c$ . Note that $R$ is invertible when $c\neq 0$ and that $R\inv$ is the diagonal matrix whose $j^{th}$ entry is $\frac {1}{c}$ and whose other diagonal entries are $1$ . For example $\left (\begin {array}{ccc} 1 & 0 & 0\\ 0 & 1 & 0 \\ 0 & 0 & 2\end {array}\right ) \left (\begin {array}{ccc} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end {array}\right ) = \left (\begin {array}{ccc} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23} \\ 2a_{31} & 2a_{32} & 2a_{33} \end {array}\right ),$ multiplies the $3^{rd}$ row by $2$ .

Next we show that the elementary row operation that swaps two rows may also be thought of as matrix multiplication. Let $R=(r_{kl})$ be the matrix that deviates from the identity matrix by changing in the four entries:

$\begin{eqnarray*} r_{ii} & = & 0 \\ r_{jj} & = & 0\\ r_{ij} & = & 1 \\ r_{ji} & = & 1 \end{eqnarray*}$

A calculation shows that $RA$ is the matrix obtained from $A$ by swapping the $i^{th}$ and $j^{th}$ rows. For example, $\left (\begin {array}{ccc} 0 & 0 & 1\\ 0 & 1 & 0 \\ 1 & 0 & 0\end {array}\right ) \left (\begin {array}{ccc} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end {array}\right ) = \left (\begin {array}{ccc} a_{31} & a_{32} & a_{33}\\ a_{21} & a_{22} & a_{23} \\ a_{11} & a_{12} & a_{13} \end {array}\right ),$ which swaps the $1^{st}$ and $3^{rd}$ rows. Another calculation shows that $R^2=I_n$ and hence that $R$ is invertible since $R\inv =R$ .

Finally, we claim that adding $c$ times the $i^{th}$ row of $A$ to the $j^{th}$ row of $A$ can be viewed as matrix multiplication. Let $E_{k\ell }$ be the matrix all of whose entries are $0$ except for the entry in the $k^{th}$ row and $\ell ^{th}$ column which is $1$ . Then $R=I_n+cE_{ij}$ has the property that $RA$ is the matrix obtained by adding $c$ times the $j^{th}$ row of $A$ to the $i^{th}$ row. We can verify by multiplication that $R$ is invertible and that $R\inv =I_n-cE_{ij}$ . More precisely, $(I_n+cE_{ij})(I_n-cE_{ij})=I_n+cE_{ij}-cE_{ij}-c^2E_{ij}^2=I_n,$ since $E_{ij}^2 = O$ for $i\not = j$ . For example,

$\begin{eqnarray*} (I_3 + 5E_{12})A & = & \left(\begin{array}{ccc} 1 & 5 & 0\\ 0 & 1 & 0 \\ 0 & 0 & 1\end{array}\right) \left(\begin{array}{ccc} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{array}\right) \\ & = & \left(\begin{array}{ccc} a_{11}+5a_{21} & a_{12}+5a_{22} & a_{13}+5a_{23} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{array}\right), \end{eqnarray*}$

adds $5$ times the $2^{nd}$ row to the $1^{st}$ row. $\blacksquare$

Determinants of Elementary Row Matrices

The determinant of a swap matrix is $-1$ .
The determinant of the matrix that adds a multiple of one row to another is $1$ .
The determinant of the matrix that multiplies one row by $c$ is $c$ .

Proof

The matrix that swaps the $i^{th}$ row with the $j^{th}$ row is the matrix whose nonzero elements are $a_{kk}=1$ where $k\neq i,j$ and $a_{ij}=1=a_{ji}$ . Using a similar argument as in (??) we see that the determinants of these matrices are equal to $-1$ .

The matrix that adds a multiple of one row to another is triangular (either upper or lower) and has $1$ ’s on the diagonal. Thus property (a) in Definition ?? implies that the determinants of these matrices are equal to $1$ .

Finally, the matrix that multiplies the $i^{th}$ row by $c\neq 0$ is a diagonal matrix all of whose diagonal entries are $1$ except for $a_{ii}=c$ . Again property (a) implies that the determinant of this matrix is $c\neq 0$ . $\blacksquare$

Computation of Determinants

We now show how to compute the determinant of any $n\times n$ matrix $A$ using elementary row operations and Definition ??. It follows from Proposition ?? that every elementary row operation on $A$ may be performed by premultiplying $A$ by an elementary row matrix.

For each matrix $A$ there is a unique reduced echelon form matrix $E$ and a sequence of elementary row matrices $R_1\ldots R_s$ such that

$\begin{equation} \label{e:rowreduction} E = R_s\cdots R_1A. \end{equation}$ It follows from Definition ??(c) that we can compute the determinant of $A$ once we know the determinants of reduced echelon form matrices and the determinants of elementary row matrices. In particular $\begin{equation} \label{e:detformula} \det(A) = \det(E)/(\det(R_1)\cdots\det(R_s)). \end{equation}$

It is easy to compute the determinant of any matrix in reduced echelon form using Definition ??(a) since all reduced echelon form $n\times n$ matrices are upper triangular. Lemma ?? tells us how to compute the determinants of elementary row matrices. This discussion proves:

If a determinant function exists for $n\times n$ matrices, then it is unique.

We still need to show that determinant functions exist when $n>2$ . More precisely, we know that the reduced echelon form matrix $E$ is uniquely defined from $A$ (Chapter ??, Theorem ??), but there is more than one way to perform elementary row operations on $A$ to get to $E$ . Thus, we can write $A$ in the form (??) in many different ways, and these different decompositions might lead to different values for $\det A$ . (They don’t.)

An Example of Determinants by Row Reduction

As a practical matter we row reduce a square matrix $A$ by premultiplying $A$ by an elementary row matrix $R_j$ . Thus

$\begin{equation} \label{e:pracdet} \det(A) = \frac{1}{\det(R_j)} \det (R_j A). \end{equation}$ We use this approach to compute the determinant of the $4\times 4$ matrix $A = \left (\begin {array}{rrrr} 0 & 2 & 10 & -2 \\ 1 & 2 & 4 & 0\\ 1 & 6 & 1 & -2 \\ 2 & 1 & 1 & 0 \end {array}\right ).$ The idea is to use (??) to keep track of the determinant while row reducing $A$ to upper triangular form. For instance, swapping rows changes the sign of the determinant; so $\det (A) = -\det \left (\begin {array}{rrrr} 1 & 2 & 4 & 0\\ 0 & 2 & 10 & -2 \\ 1 & 6 & 1 & -2 \\ 2 & 1 & 1 & 0 \end {array}\right ).$ Adding multiples of one row to another leaves the determinant unchanged; so $\det (A) = -\det \left (\begin {array}{rrrr} 1 & 2 & 4 & 0\\ 0 & 2 & 10 & -2 \\ 0 & 4 & -3 & -2 \\ 0 & -3 & -7 & 0 \end {array}\right ).$ Multiplying a row by a scalar $c$ corresponds to an elementary row matrix whose determinant is $c$ . To make sure that we do not change the value of $\det (A)$ , we have to divide the determinant by $c$ as we multiply a row of $A$ by $c$ . So as we divide the second row of the matrix by $2$ , we multiply the whole result by $2$ , obtaining $\det (A) = -2\det \left (\begin {array}{rrrr} 1 & 2 & 4 & 0\\ 0 & 1 & 5 & -1 \\ 0 & 4 & -3 & -2 \\ 0 & -3 & -7 & 0 \end {array}\right ).$ We continue row reduction by zeroing out the last two entries in the $2^{nd}$ column, obtaining $\begin{align*} \det(A) &= -2\det\left(\begin{array}{rrrr} 1 & 2 & 4 & 0\\ 0 & 1 & 5 & -1 \\ 0 & 0 & -23 & 2 \\ 0 & 0 & 8 & -3 \end{array}\right) \\ &= 46\det\left(\begin{array}{rrrr} 1 & 2 & 4 & 0\\ 0 & 1 & 5 & -1 \\ 0 & 0 & 1 & -\frac{2}{23} \\ 0 & 0 & 8 & -3 \end{array}\right). \end{align*}$

Thus $\det (A) = 46\det \left (\begin {array}{rrrr} 1 & 2 & 4 & 0\\ 0 & 1 & 5 & -1 \\ 0 & 0 & 1 & -\frac {2}{23} \\ 0 & 0 & 0 & -\frac {53}{23} \end {array}\right ) = -106.$

Determinants and Inverses

We end this subsection with an important observation about the determinant function. This observation generalizes to dimension $n$ Corollary ?? of Chapter ??.

An $n\times n$ matrix $A$ is invertible if and only if $\det (A)\neq 0$ . Moreover, if $A\inv$ exists, then $\begin{equation} \label{E:detinv} \det A\inv = \frac{1}{\det A}. \end{equation}$

Proof: If $A$ is invertible, then $\det (A)\det (A\inv ) = \det (AA\inv ) = \det (I_n) =1.$ Thus $\det (A)\neq 0$ and (??) is valid. In particular, the determinants of elementary row matrices are nonzero, since they are all invertible. (This point was proved by direct calculation in Lemma ??.)
If $A$ is singular, then $A$ is row equivalent to a non-identity reduced echelon form matrix $E$ whose determinant is zero (since $E$ is upper triangular and its last diagonal entry is zero). So it follows from (??) that $0=\det (E) = \det (R_1)\cdots \det (R_s)\det (A)$ Since $\det (R_j)\neq 0$ , it follows that $\det (A)=0$ . $\blacksquare$

If the rows of an $n\times n$ matrix $A$ are linearly dependent (for example, if one row of $A$ is a scalar multiple of another row of $A$ ), then $\det (A)=0$ .

An Inductive Formula for Determinants

In this subsection we present an inductive formula for the determinant — that is, we assume that the determinant is known for square $(n-1)\times (n-1)$ matrices and use this formula to define the determinant for $n\times n$ matrices. This inductive formula is called expansion by cofactors.

Let $A=(a_{ij})$ be an $n\times n$ matrix. Let $A_{ij}$ be the $(n-1)\times (n-1)$ matrix formed from $A$ by deleting the $i^{th}$ row and the $j^{th}$ column. The matrices $(-1)^{i+j}A_{ij}$ are called cofactor matrices of $A$ .

Inductively we define the determinant of an $n\times n$ matrix $A$ by:

$\begin{align} \det(A) & = \sum^n_{j=1} (-1)^{1+j}a_{1j}\det(A_{1j}) \nonumber \\ & = a_{11}\det(A_{11})-a_{12}\det(A_{12})+\cdots \nonumber\\ & \quad +(-1)^{n+1}a_{1n}\det(A_{1n}). \label{e:inductdet} \end{align}$

In Appendix ?? we show that the determinant function defined by (??) satisfies all properties of a determinant function. Formula (??) is also called expansion by cofactors along the $1^{st}$ row, since the $a_{1j}$ are taken from the $1^{st}$ row of $A$ . Since $\det (A)=\det (A^t)$ , it follows that if (??) is valid as an inductive definition of determinant, then expansion by cofactors along the $1^{st}$ column is also valid. That is,

$\begin{equation} \label{e:inductdetc} \det(A) = a_{11}\det(A_{11})-a_{21}\det(A_{21})+\cdots+(-1)^{n+1}a_{n1}\det(A_{n1}). \end{equation}$

We now explore some of the consequences of this definition, beginning with determinants of small matrices. For example, Definition ??(a) implies that the determinant of a $1\times 1$ matrix is just $\det (a) = a.$ Therefore, using (??), the determinant of a $2\times 2$ matrix is: $\det \left (\begin {array}{cc} a_{11} & a_{12}\\a_{21} & a_{22} \end {array}\right ) = a_{11}\det (a_{22}) - a_{12}\det (a_{21}) = a_{11}a_{22} - a_{12}a_{21},$ which is just the formula for determinants of $2\times 2$ matrices given in (??).

Similarly, we can now find a formula for the determinant of $3\times 3$ matrices $A$ as follows.

$\begin{align} \det(A) & = a_{11} \det \left(\begin{array}{cc} a_{22} & a_{23}\\a_{32} & a_{33} \end{array}\right) - a_{12} \det \left(\begin{array}{cc} a_{21} & a_{23}\\a_{31} & a_{33} \end{array}\right) \nonumber\\ &\quad + a_{13} \det\left(\begin{array}{cc} a_{21} & a_{22}\\a_{31} & a_{32} \end{array}\right) \nonumber\\ & = a_{11}a_{22}a_{33} + a_{12}a_{23}a_{31} + a_{13}a_{21}a_{32} \nonumber\\ &\quad - a_{11}a_{23}a_{32} - a_{12}a_{21}a_{33} - a_{13}a_{22}a_{31}. \label{e:det3} \end{align}$

As an example, compute $\det \left (\begin {array}{rrr} 2 & 1 & 4\\ 1 & -1 & 3\\ 5 & 6 & -2 \end {array}\right )$ using formula (??) as

$\begin{align*} 2(-1)(-2) & + 1\cdot3\cdot5 + 4\cdot6\cdot1 -4(-1)5 -3\cdot6\cdot2 - (-2)1\cdot1 \\ &= 4+15+24+20 -36 +2 = 29. \end{align*}$

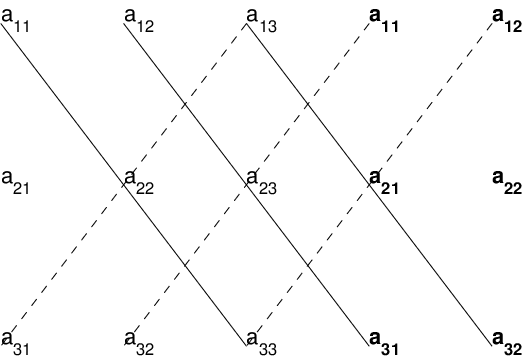
There is a visual mnemonic for remembering how to compute the six terms in formula (??) for the determinant of $3\times 3$ matrices. Write the matrix as a $3\times 5$ array by repeating the first two columns, as shown in bold face in Figure ??:

Figure 1: Mnemonic for computation of determinants of $3\times 3$ matrices.

Then add the product of terms connected by solid lines sloping down and to the right and subtract the products of terms connected by dashed lines sloping up and to the right. Warning: this nice crisscross algorithm for computing determinants of $3\times 3$ matrices does not generalize to $n\times n$ matrices.

When computing determinants of $n\times n$ matrices when $n>3$ , it is usually more efficient to compute the determinant using row reduction rather than by using formula (??). In the appendix to this chapter, Section ??, we verify that formula (??) actually satisfies the three properties of a determinant, thus completing the proof of Theorem ??.

An interesting and useful formula for reducing the effort in computing determinants is given by the following formula.

Let $A$ be an $n\times n$ matrix of the form $A=\mattwo {B}{0}{C}{D},$ where $B$ is a $k\times k$ matrix and $D$ is an $(n-k)\times (n-k)$ matrix. Then $\det (A)=\det (B)\det (D).$

Proof: We prove this result using (??) coupled with induction. Assume that this lemma is valid or all $(n-1)\times (n-1)$ matrices of the appropriate form. Now use (??) to compute
$\begin{eqnarray*} \det(A) & = & a_{11}\det(A_{11})-a_{12}\det(A_{12}) + \cdots\pm a_{1n}\det(A_{1n}) \\ & = & b_{11}\det(A_{11})-b_{12}\det(A_{12}) + \cdots\pm b_{1k}\det(A_{1k}). \end{eqnarray*}$
Note that the cofactor matrices $A_{1j}$ are obtained from $A$ by deleting the $1^{st}$ row and the $j^{th}$ column. These matrices all have the form $A_{1j} = \mattwo {B_{1j}}{0}{C_j}{D},$ where $C_j$ is obtained from $C$ by deleting the $j^{th}$ column. By induction on $k$ $\det (A_{1j}) = \det (B_{1j})\det (D).$ It follows that $\begin{align*} \det(A) & = \left(b_{11}\det(B_{11})-b_{12}\det(B_{12}) + \cdots \right. \\ &\quad \left. \pm b_{1k}\det(B_{1k})\right)\det(D) \\ & = \det(B)\det(D), \end{align*}$
as desired. $\blacksquare$

Determinants in MATLAB

The determinant function has been preprogrammed in MATLAB and is quite easy to use. For example, typing e8_1_11 will load the matrix

$\begin{equation} \label{e:A4x4} A = \left(\begin{array}{rrrr} 1 & 2 & 3 & 0\\ 2 & 1 & 4 & 1\\ -2 & -1 & 0 & 1\\ -1 & 0 & -2 & 3 \end{array} \right). \end{matlabEquation} To compute the determinant of $A$ just type {\tt det(A)} and obtain the answer \index{\computer!det} \begin{verbatim} ans = -46 \end{verbatim} Alternatively, we can use row reduction techniques in \Matlab to compute the determinant of $A$ --- just to test the theory that we have developed. Note that to compute the determinant we do not need to row reduce to reduced echelon form\index{echelon form!reduced} --- we need only reduce to an upper triangular matrix. This can always be done by successively adding multiples of one row to another --- an operation that does not change the determinant. For example, to clear the entries in the $1^{st}$ column below the $1^{st}$ row, type \begin{verbatim} A(2,:) = A(2,:) - 2*A(1,:); A(3,:) = A(3,:) + 2*A(1,:); A(4,:) = A(4,:) + A(1,:) \end{verbatim} obtaining \begin{verbatim} A = 1 2 3 0 0 -3 -2 1 0 3 6 1 0 2 1 3 \end{verbatim} To clear the $2^{nd}$ column below the $2^{nd}$ row type \begin{verbatim} A(3,:) = A(3,:) + A(2,:);A(4,:) = A(4,:) - A(4,2)*A(2,:)/A(2,2)\end{verbatim} obtaining \begin{verbatim} A = 1.0000 2.0000 3.0000 0 0 -3.0000 -2.0000 1.0000 0 0 4.0000 2.0000 0 0 -0.3333 3.6667 \end{verbatim} Finally, to clear the entry $(4,3)$ type \begin{verbatim} A(4,:) = A(4,:) -A(4,3)*A(3,:)/A(3,3)\end{verbatim} to obtain \begin{verbatim} A = 1.0000 2.0000 3.0000 0 0 -3.0000 -2.0000 1.0000 0 0 4.0000 2.0000 0 0 0 3.8333 \end{verbatim} To evaluate the determinant of $A$, which is now an upper triangular matrix, type \begin{verbatim} A(1,1)*A(2,2)*A(3,3)*A(4,4)\end{verbatim} obtaining \begin{verbatim} ans = -46 \end{verbatim} as expected. \EXER \TEXER \noindent In Exercises~\ref{c10.1.1a} -- \ref{c10.1.1c} compute the determinants of the given matrix. \begin{exercise} \label{c10.1.1a} $A = \left(\begin{array}{rrr} -2 & 1 & 0 \\ 4 & 5& 0 \\ 1 & 0 & 2 \end{array} \right)$. \end{exercise} \begin{exercise} \label{c10.1.1b} $B = \left(\begin{array}{rrrr} 1 & 0 & 2 & 3 \\ -1 & -2 & 3 & 2 \\ 4 & -2 & 0 & 3 \\ 1 & 2 & 0 & -3 \end{array} \right)$. \end{exercise} \begin{exercise} \label{c10.1.1c} $C = \left(\begin{array}{rrrrr} 2 & 1 & -1 & 0 & 0 \\ 1 & -2 & 3 & 0 & 0 \\ -3 & 2 & -2 & 0 & 0 \\ 1 & 1 & -1 & 2 & 4 \\ 0 & 2 & 3 & -1 & -3 \end{array} \right)$. \end{exercise} \begin{exercise} \label{c10.1.2} Find $\det(A\inv)$ where $A = \left(\begin{array}{rrr} -2 & -3 & 2 \\ 4 & 1 & 3 \\ -1 & 1 & 1 \end{array} \right)$. \end{exercise} \begin{exercise} \label{c10.1.3} Show that the determinants of similar $n\times n$ matrices are equal. \end{exercise} \noindent In Exercises~\ref{c10.1.4} -- \ref{c10.1.5b} use row reduction to compute the determinant of the given matrix. \begin{exercise} \label{c10.1.4} $A = \left(\begin{array}{rrr} -1 & -2 & 1 \\ 3 & 1 & 3 \\ -1 & 1 & 1 \end{array} \right)$. \end{exercise} \begin{exercise} \label{c10.1.5a} $B = \left(\begin{array}{rrrr} 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & -1 \\ 1 & 0 & -1 & 0 \\ 0 & 1 & 0 & 1 \end{array}\right)$. \end{exercise} \begin{exercise} \label{c10.1.5b} $C = \left(\begin{array}{rrrr} 1 & 2 & 0 & 1 \\ 0 & 2 & 1 & 0 \\ -2 & -3 & 3 & -1 \\ 1 & 0 & 5 & 2 \end{array}\right)$. \end{exercise} \begin{exercise} \label{c10.1.6} Let \[ A = \left(\begin{array}{rrr} 2 & -1 & 0 \\ 0 & 3 & 0 \\ 1 & 5 & 3 \end{array} \right) \AND B = \left(\begin{array}{rrr} 2 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & 3 \end{array} \right). \] \begin{itemize} \item[(a)] For what values of $\lambda$ is $\det(\lambda A-B)=0$? \item[(b)] Is there a vector $x$ for which $Ax=Bx$? \end{itemize} \end{exercise} \noindent In Exercises~\ref{c10.1.a7a} -- \ref{c10.1.a7b} verify that the given matrix has determinant $-1$. \begin{exercise} \label{c10.1.a7a} $A = \left( \begin{array}{rrr} 1 & 0 & 0\\ 0 & 0 & 1\\ 0 & 1 & 0 \end{array} \right)$. \end{exercise} \begin{exercise} \label{c10.1.a7b} $B = \left( \begin{array}{rrr} 0 & 0 & 1\\ 0 & 1 & 0\\ 1 & 0 & 0 \end{array} \right)$. \end{exercise} \begin{exercise} \label{c10.1.b7a} Compute the cofactor matrices $A_{13}, A_{22}, A_{21}$ when $A = \left( \begin{array}{rrr} 3 & 2 & -4\\ 0 & 1 & 5\\ 0 & 0 & 6\end{array} \right)$. \end{exercise} \begin{exercise} \label{c10.1.b7b} Compute the cofactor matrices $B_{11}, B_{23}, B_{43}$ when $B = \left( \begin{array}{rrrr} 0 & 2 & -4 & 5\\ -1 & 7 & -2 & 10\\ 0 & 0 & 0 & -1\\ 3 & 4 & 2 & -10 \end{array} \right)$. \end{exercise} \begin{exercise} \label{c10.1.c7} Find values of $\lambda$ where the determinant of the matrix \[ A_\lambda = \left( \begin{array}{ccr} \lambda -1 & 0 & -1\\ 0 & \lambda -1 & 1\\ -1 & 1 & \lambda \end{array} \right) \] vanishes. \end{exercise} \begin{exercise} \label{c10.1.c8} Suppose that two $n\times p$ matrices $A$ and $B$ are row equivalent. \index{row!equivalent} Show that there is an invertible $n\times n$ matrix $P$ such that $B = PA$. \end{exercise} \begin{exercise} \label{c10.1.c9} Let $A$ be an invertible $n\times n$ matrix and let $b\in\R^n$ be a column vector. Let $B_j$ be the $n\times n$ matrix obtained from $A$ by replacing the $j^{th}$ column of $A$ by the vector $b$. Let $x=(x_1,\ldots,x_n)^t$ be the unique solution to $Ax=b$. Then Cramer's rule \index{Cramer's rule} states that \begin{equation} \label{E:cramer2} x_j = \frac{\det(B_j)}{\det(A)}. \end{equation}$ Prove Cramer’s rule. Hint: Let $A_j$ be the $j^{th}$ column of $A$ so that $A_j = Ae_j$ . Show that $B_j = A (e_1|\cdots |e_{j-1}|x|e_{j+1}|\cdots |e_n).$ Using this product, compute the determinant of $B_j$ and verify (??).

Determinants of <![CDATA[ 2\times 2 ]]> Matrices