Exponential

$\newenvironment {prompt}{}{} \newcommand {\ungraded }[0]{} \newcommand {\todo }[0]{} \newcommand {\oiint }[0]{{\large \bigcirc }\kern -1.56em\iint } \newcommand {\mooculus }[0]{\textsf {\textbf {MOOC}\textnormal {\textsf {ULUS}}}} \newcommand {\npnoround }[0]{\nprounddigits {-1}} \newcommand {\npnoroundexp }[0]{\nproundexpdigits {-1}} \newcommand {\npunitcommand }[1]{\ensuremath {\mathrm {#1}}} \newcommand {\sagemath }[0]{\textsf {SageMath}} \newcommand {\surfaceColor }[0]{violet} \newcommand {\surfaceColorTwo }[0]{redyellow} \newcommand {\sliceColor }[0]{greenyellow} \newcommand {\vector }[1]{\left \langle #1\right \rangle } \newcommand {\sectionOutcomes }[0]{} \newcommand {\HyperFirstAtBeginDocument }[0]{\AtBeginDocument }$

percentage growth

The defining characteristic of linear functions is that the pairs experience a constant growth rate. If you calculate the rate of change between any two pairs, $(a, f(a))$ and $(b, f(b))$ , in the function, you get the same value, $m$ .

$\frac {f(b)-f(a)}{b-a} = m$

This led to the equation or formula for linear functions: $f(x) = m(x-a) + f(a)$

Said another way: If you move a fixed amount anywhere in the domain, $\Delta x$ , then the function always grows by a proportionally fixed amount, $f(x + \Delta x) - f(x) = m(\Delta x)$ . This fixed growth rate is always the same multiple of the change in the domain. That multiple is the constant growth rate.

$\blacktriangleright$ Exponential functions are similar, but it is their percentage growth rate that is constant.

Cancer Cells

https://www.ncbi.nlm.nih.gov/pmc/articles/PMC6695196/

Abstract:. Most models of cancer cell population expansion assume exponential growth kinetics at low cell densities, with deviations to account for observed slowing of growth rate only at higher densities due to limited resources such as space and nutrients. [...]

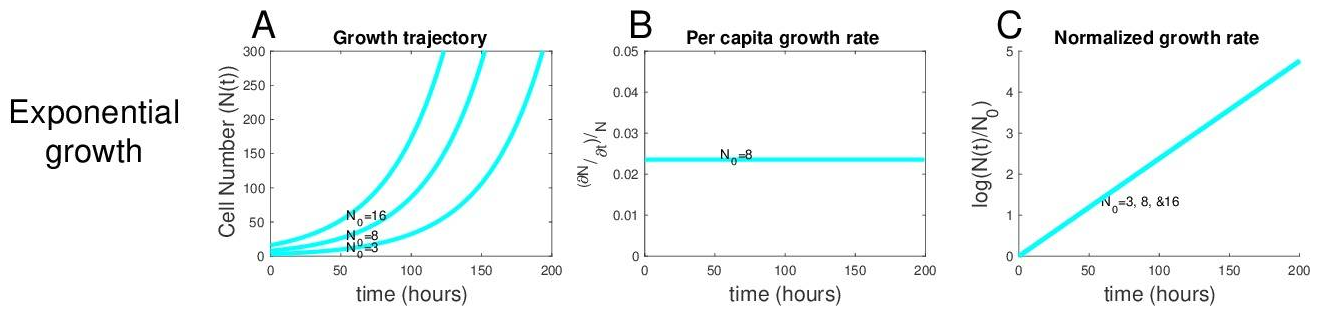
The number of cancer cells is given by $N(t) = N_0 \, e^{g \, t}$ .

The graphs above show $N_0 = 3, 8, 16$

The first graph illustrate classical exponential growth.

The second graph captures the “per capita growth rate”. This would be the growth in the number of cancer cells divided by the number of cancer cells. This gives the percentage growth. The graph shows a constant function, because the percentage growth rate is a constant.

The third graph shows the logarithm of the first graph, which turns out to be a linear function.

The growth of an exponential function, $g(t)$ over the interval $[a, b]$ is $g(b)-g(a)$ . To get a percentage, we compare this back to the starting value, $g(a)$ :

$\frac {g(b)-g(a)}{g(a)}$

And, then to get the percentage growth rate we average over the interval

$\frac {\frac {g(b)-g(a)}{g(a)}}{b-a}$

For an exponential function, this is constant

$\frac {\frac {g(b)-g(a)}{g(a)}}{b-a} = r$

$\frac {g(b)-g(a)}{g(a)(b-a)} = r$

Let’s build such a function up from a given value of $g(0)$ .

Moving from $0$ to $1$ gives

$\frac {\frac {g(1)-g(0)}{g(0)}}{1-0} = r$

$g(1)-g(0) = r \, g(0)$

$g(1) = r \, g(0) + g(0)$

$g(1) = g(0) (r + 1)$

Moving from $1$ to $2$ gives

$g(2) - g(1) = g(1) r$

$g(2) = g(1) (r + 1)$

$g(2) = g(0) (r + 1) (r + 1)$

$g(2) = g(0) (r + 1)^2$

Moving from $2$ to $3$ gives

$g(3) = g(0) (r + 1)^3$

In general, formulas for exponential functions look like

$g(t) = g(0) \cdot a^t$

Exponential Functions

Basic Exponential Functions

Basic exponential functions are those functions that exhibit a constant percentage rate of change. Their formulas look like

$f(x) = A \cdot b^x$

where $A$ is a nonzero real number, and $b$ is a positive real number.

Said another way: If you move a fixed amount in the domain, $\Delta x$ , then the change in an exponential function, $k \cdot a^{x + \Delta x} - k \cdot a^x = k \cdot a^x (a^{\Delta x} - 1)$ , is the same fixed multiple of the function value.

Linear growth is a fixed multiple of the change in domain value. It is independent of the function value.
Exponential growth (for a fixed change in domain value) is a fixed multiple of the function value.

There are two types of exponential functions corresponding to $0<a<1$ or $1<a$ .

If $0<a<1$ , then greater positive exponents make the function value smaller.
In the other direction, a negative exponent essentially gives us the reciprocal of $a$ , which would be greater than $1$ here. Therefore, greater negative exponents result in bigger function values.
If $1<a$ , then greater positive exponents make the function value bigger.
In the other direction, a negative exponent essentially gives us the reciprocal of $a$ , which would be less than $1$ here. Therefore, greater negative exponents result in smaller postive function values.

The graphs of $y = Y(x) = 3 \cdot \left (\frac {1}{2}\right )^x$ and $z = W(t) = 3 \cdot 2^t$ are shown below.

There is no vertical asymptote. The domain of exponential functions is all real numbers. $y=0$ is a horizontal asymptote on both graphs. The sign of an exponential function is given by the coefficient.

Since these formulas are centered around the exponent, they follow the exponent rules:

$a^n \cdot a^m = a^{n+m}$
$\frac {a^n}{a^m} = a^{n-m}$
$(a^n)^m = a^{n \cdot m}$
$a^n \cdot b^n = (a \cdot b)^n$
$\frac {a^n}{b^n} = \left (\frac {a}{b}\right )^n$

Let $T(f) = 4 \cdot 3^f$ . Evaluate the following.

$T(0) = \answer {4}$
$T(1) = \answer {12}$
$T(-1) = \answer {\frac {4}{3}}$

Exponential Functions

Exponential functions are those functions that can be represented by formulas of the form

$f(x) = A \cdot b^{B \, x + C}$

where $A$ , $B$ , and $C$ are real numbers, $A$ is a nonzero real number, and $b$ is a positive real number.

This is the most general form of an exponential function. It is equivalent to the basic form, meaning it can be transformed into the basic form using our exponent rules.

$f(x) = A \cdot b^{B \, x + C}$

$f(x) = A \cdot b^{B \, x} \cdot b^C$

$f(x) = A \cdot (b^{B})^x \cdot b^C$

$f(x) = A \cdot b^C \cdot (b^{B})^x = a \cdot r^x$

$A \cdot b^C$ is the new leading coefficient.

$b^{B}$ is the new base.

Basic Exponential Function

For practical purposes, we should have an example in our head and then compare other exponential functions back to it.

Our example is $exp(x) = e^x$ .

$e > 1$ , which means this exponential function only has positive values on its domain, $(-\infty , \infty )$ . It is an increasing function. Its range is $(0, \infty )$ .

Note: You could select other bases besides $e$ . Most people like a base greater than $1$ .

It we have the chanracteristics of this exponential function memorized, then we can compare other exponential functions back to this one.

Alternative Basic Exponential Function

We have four general behaviors of exponential functions, which we will investigate in this course. By changing the sign of the leading coefficent or the leading coefficient in the exponent, you can get any of the four types.

$e^x$
$e^{-x}$
$-e^x$
$-e^{-x}$

If you memorize the characteristics of one of these, then you can deduce the characteristics of all of them.

For most people, memorizing the characteristics of $e^x$ is the easiest.

Exponential functions are those functions that CAN be described with a formula like

$A \cdot r^x$

Using exponent rules, we can rewrite any exponential formula into this form. Therefore, it is nice to memorize the charcateristics of one of these basic forms and then compare all others back to it.

Even if $r<1$ , the base can be rewritten as $(r^{-1})^{-1}$ . The first $-1$ exponent stays with the $r$ , to make $r^{-1}>1$ . The second $-1$ moves up to the exponent and changes the sign of the exponent.

Example:

$\left ( \frac {1}{3} \right ) = \left ( \left ( \frac {1}{3} \right )^{-1} \right )^{-1} = ( 3 )^{-1}$

$2 \left ( \frac {1}{3} \right )^{5-6x} = 2 \left ( ( 3 )^{-1} \right )^{5-6x} = 2 (3)^{(-1)(5-6x)} = 2 (3)^{-5+6x}$

Shifted Exponential Functions

Shifted Exponential Functions

Shifted exponential functions are exponential functions with a number added on.

$f(x) = A \cdot r^{B \, x + C} + D$

where $A$ , $B$ , $C$ , and $D$ are real numbers, $A \ne 0$ and $B \ne 0$ and $D \ne 0$ , and $r$ is a positive real number.

The main different between shifted exponential and exponential functions is that while exponential functions do not have zeros, a shifted exponential function may have a zero.

Here is the graph of $g(x) = 2^x - 3$ .

$\log _2(3)$ is the zero of $g(x)$ .

ooooo=-=-=-=-=-=-=-=-=-=-=-=-=ooOoo=-=-=-=-=-=-=-=-=-=-=-=-=ooooo
more examples can be found by following this link
More Examples of Elementary Functions