Function Properties

$\newenvironment {prompt}{}{} \newcommand {\ungraded }[0]{} \newcommand {\todo }[0]{} \newcommand {\oiint }[0]{{\large \bigcirc }\kern -1.56em\iint } \newcommand {\mooculus }[0]{\textsf {\textbf {MOOC}\textnormal {\textsf {ULUS}}}} \newcommand {\npnoround }[0]{\nprounddigits {-1}} \newcommand {\npnoroundexp }[0]{\nproundexpdigits {-1}} \newcommand {\npunitcommand }[1]{\ensuremath {\mathrm {#1}}} \newcommand {\sagemath }[0]{\textsf {SageMath}} \newcommand {\surfaceColor }[0]{violet} \newcommand {\surfaceColorTwo }[0]{redyellow} \newcommand {\sliceColor }[0]{greenyellow} \newcommand {\vector }[1]{\left \langle #1\right \rangle } \newcommand {\sectionOutcomes }[0]{} \newcommand {\HyperFirstAtBeginDocument }[0]{\AtBeginDocument }$

characteristics, features

Numbers have properties and we use these properties to define sets of numbers.

Evens: $\{ \cdots , -6, -4, -2, 0, 2, 4, 6, \cdots \} = \{ 2n \, | \, n \in \mathbb {Z} \}$
Squares: $\{ 1, 4, 9, 16, \cdots \} = \{ n^2 \, | \, n \in \mathbb {N} \}$
Primes: $\{ 2, 3, 5, 7, 11, \cdots \}$

Once we know that a number belongs to one of these sets, i.e. has the property, then we automatically know some information about the number.

$\blacktriangleright$ Same with functions.

A major goal of this course is to develop a list of function properties and define sets of functions via these properties. Once we know a function belongs to a set, then we get a lot of free information about the function.

Function Characteristics or Properties

Let’s start off with two basic properties: Onto and One-to-One.

Onto

If the range equals the codomain, then the function is said to be onto.

SuperBowlWinner

SuperBowlWinner is not an onto function.

The Cleveland Browns are in the codomain, but are not in the range of SuperBowlWinner.

Some functions are onto. Some are not.

The one and only rule for a function is that each domain item is in exactly one pair. Range items can be in multiple pairs or no pairs.

However, if the range also follows this rule, then the function is called a one-to-one function.

One-to-One

A one-to-one function is a function in which each range number is in exactly one pair.

Some functions are one-to-one. Some are not.

SuperBowlWinner

SuperBowlWinner is not a one-to-one function.

The Pittsburgh Steelers is a range team that is in multiple pairs.

StateCapitals

StateCapitals pairs U.S. states with a city that has served as the state’s capital. Its domain is U.S. states and the codomain is all U.S. cities.

This function is not well-defined, because a state may have had different capital cities depending on the year.

StateCapitals2020 pairs U.S. states with their capital city on January 1, 2020. Its domain is U.S. states and the codomain is all U.S. cities.

This is a well-defined function. It is a one-to-one function, because on January 1, 2020 no city was the capital of two states. It is not onto, since not every U.S. city is a state capital.

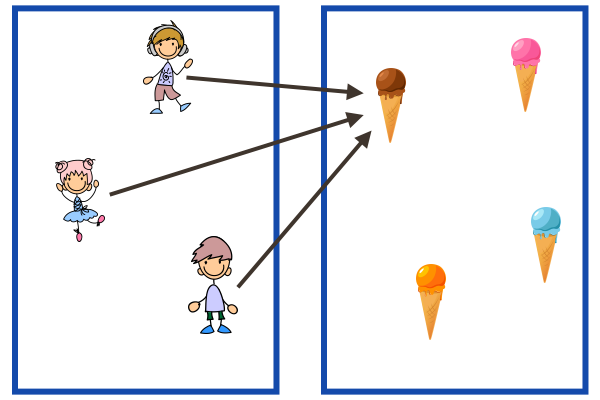
$\blacktriangleright$ Example: A function that is both onto and one-to-one.

(arrows go from the domain to the codomain.)

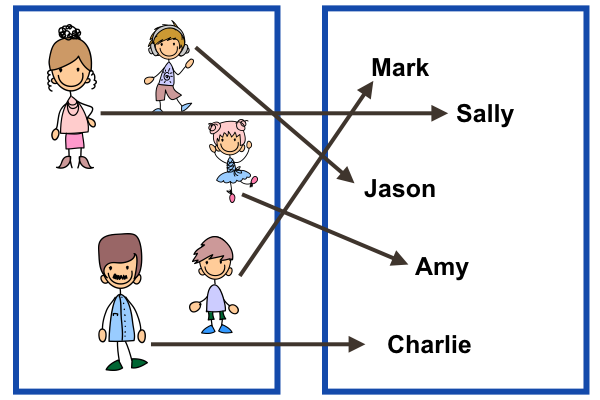
$\blacktriangleright$ Example: A function that is onto but not one-to-one.

(arrows go from the domain to the codomain.)

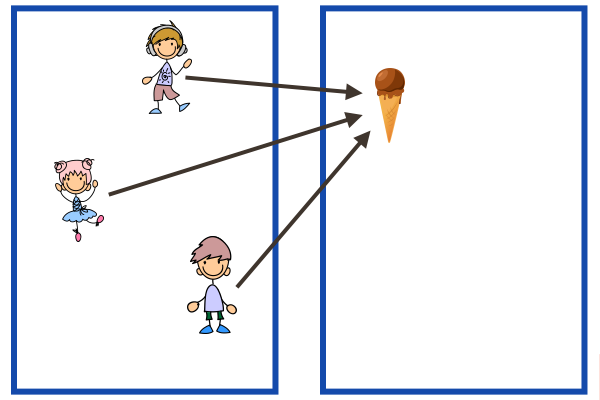
$\blacktriangleright$ Example: A function that is one-to-one but not onto.

(arrows go from the domain to the codomain.)

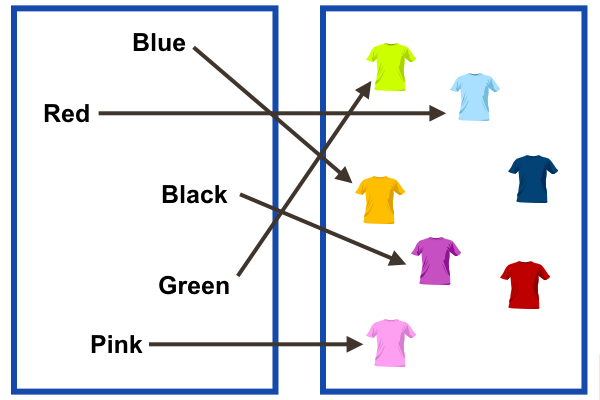
$\blacktriangleright$ Example: A function that is neither one-to-one nor onto.

(arrows go from the domain to the codomain.)

These examples illustrate that onto and one-to-one are independent properties. A function can have either property with or without the other.

ooooo=-=-=-=-=-=-=-=-=-=-=-=-=ooOoo=-=-=-=-=-=-=-=-=-=-=-=-=ooooo
more examples can be found by following this link
More Examples of Functions