$$\frac {f(b)-f(a)}{b-a} = m$$

This led to the equation or formula for linear functions: $f(x) = m(x-a) + f(a)$

Said another way: If you move a fixed amount anywhere in the domain, $\Delta x$, then the function always grows by a proportionally fixed amount, $f(x + \Delta x) - f(x) = m(\Delta x)$. This fixed growth rate is always the same multiple of the change in the domain. That multiple is the constant growth rate.

$\blacktriangleright$ Exponential functions are similar, but it is their percentage growth rate that is constant.

Cancer Cells

https://www.ncbi.nlm.nih.gov/pmc/articles/PMC6695196/

Abstract:. Most models of cancer cell population expansion assume exponential growth kinetics at low cell densities, with deviations to account for observed slowing of growth rate only at higher densities due to limited resources such as space and nutrients. [...]

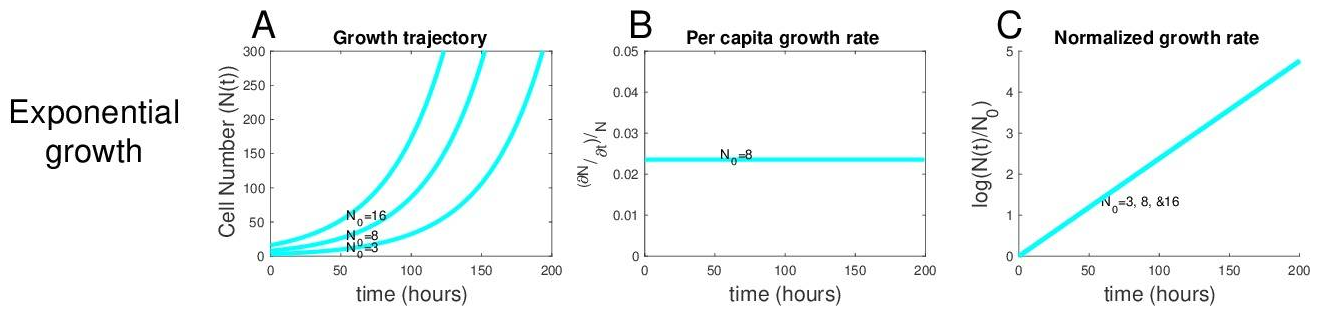
The number of cancer cells is given by $N(t) = N_0 \, e^{g \, t}$.

The graphs above show $N_0 = 3, 8, 16$

The first graph illustrate classical exponential growth.

The second graph captures the “per capita growth rate”. This would be the growth in the number of cancer cells divided by the number of cancer cells. This gives the percentage growth. The graph shows a constant function, because the percentage growth rate is a constant.

The third graph shows the logarithm of the first graph, which turns out to be a linear function.

The growth of an exponential function, $g(t)$ over the interval $[a, b]$ is $g(b)-g(a)$. To get a percentage, we compare this back to the starting value, $g(a)$:

$$\frac {g(b)-g(a)}{g(a)}$$

And, then to get the percentage growth rate we average over the interval

$$\frac {\frac {g(b)-g(a)}{g(a)}}{b-a}$$

For an exponential function, this is constant

$$\frac {\frac {g(b)-g(a)}{g(a)}}{b-a} = r$$

or

$$\frac {g(b)-g(a)}{g(a)(b-a)} = r$$

Let’s build such a function up from a given value of $g(0)$.

In general, formulas for exponential functions look like

$$g(t) = g(0) \cdot a^t$$

Exponential Functions

Said another way: If you move a fixed amount in the domain, $\Delta x$, then the change in an exponential function, $k \cdot a^{x + \Delta x} - k \cdot a^x = k \cdot a^x (a^{\Delta x} - 1)$, is the same fixed multiple of the function value.

• Linear growth is a fixed multiple of the change in domain value. It is independent of the function value.
• Exponential growth (for a fixed change in domain value) is a fixed multiple of the function value.

There are two types of exponential functions corresponding to $0<a<1$ or $1<a$.

• If $0<a<1$, then greater positive exponents make the function value smaller.
  In the other direction, a negative exponent essentially gives us the reciprocal of $a$, which would be greater than $1$ here. Therefore, greater negative exponents result in bigger function values.
  
• If $1<a$, then greater positive exponents make the function value bigger.
  In the other direction, a negative exponent essentially gives us the reciprocal of $a$, which would be less than $1$ here. Therefore, greater negative exponents result in smaller postive function values.

The graphs of $y = Y(x) = 3 \cdot \left (\frac {1}{2}\right )^x$ and $z = W(t) = 3 \cdot 2^t$ are shown below.

There is no vertical asymptote. The domain of exponential functions is all real numbers. $y=0$ is a horizontal asymptote on both graphs. The sign of an exponential function is given by the coefficient.

Since these formulas are centered around the exponent, they follow the exponent rules:

• $a^n \cdot a^m = a^{n+m}$
• $\frac {a^n}{a^m} = a^{n-m}$
• $(a^n)^m = a^{n \cdot m}$
• $a^n \cdot b^n = (a \cdot b)^n$
• $\frac {a^n}{b^n} = \left (\frac {a}{b}\right )^n$

Backwards

What if we have a function value for an exponential function and we would like to know which domain numbers are associated with it? In other words, we would like to solve

$$g(t) = k \cdot a^t = g_0$$

How would we solve for $t$?

Most function values are not going to be so obvious.

For example, solve $3^x = 17$.

We may not be able to quickly think up this number or even an approximation for it. However, we can still talk about it.

That is a specific number. We can see from the graph that there is only one such number and we could visually approximate it around $2.5$.

As with all mathematical phrases, we have shorthand notation for these desciptions.

Logarithms are exponents. They can be positive or negative.

$9^{-2} = \frac {1}{81}$, therefore $\log _{9}\left (\frac {1}{81}\right ) = -2$

We also know that raising a positve number to any exponent cannot produce a negative number or $0$. Therefore, the number inside the logarithm must be positive

It sounds like we have a new category of functions.

Here is the graph of $y = L(x) = \log _2(x)$.

The intercept is $(1,0)$, because $\log _2(1) = 0$, because $2^0 = 1$.

On the interval $(0,1)$, we are looking at $\log _2(x)$ for $0<x<1$. Remember, $\log _2(x)$ is the number you raise $2$ to, to get $x$, but here $0<x<1$. Therefore, $2$ needs a negative exponent or $\log _2(x) < 0$. And, the smaller (closer to $0$) you want $x$, the bigger the negative exponent.

If we switch the base from something greater than $1$, to something less than $1$, then all of the exponents flip. The graph flips.

Here is the graph of $y = L(x) = \log _{\tfrac {1}{2}}(x)$.

The intercept is $(1,0)$, because $\log _{\tfrac {1}{2}}(1) = 0$, because $\left (\frac {1}{2}\right )^0 = 1$.

On the interval $(0,1)$, we are looking at $\log _{\tfrac {1}{2}}(x)$ for $0<x<1$. Now we just need large positive exponents of $\frac {1}{2}$ to get small numbers. On the other hand, to get large positive numbers we need to raise $\frac {1}{2}$ to negative powers.