In this section, we will derive the equation for the reflection coefficient. The reflection coefficient relates the forward-going voltage with reflected voltage.
Reflection coefficient at the load
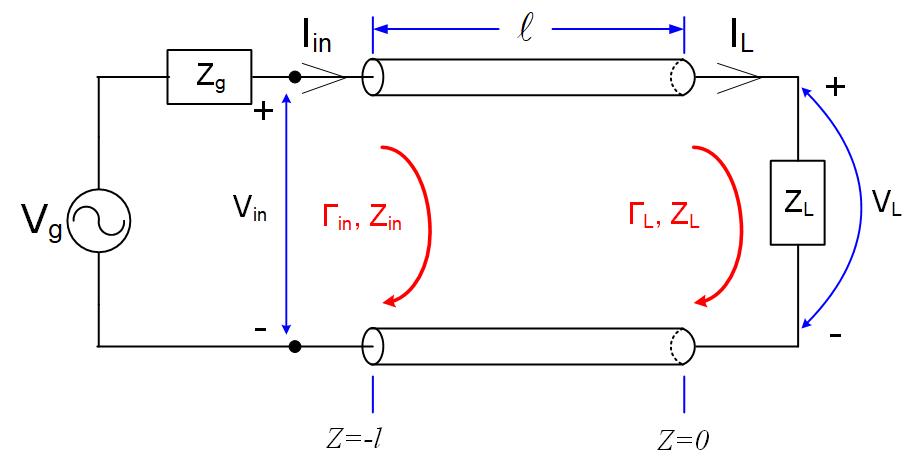
Equations eq:RCvtl-eq:RCctl represent the voltage and current on a lossless transmission line shown in Figure fig:RCTLCircuit.
We set up the z-axis so that the is at the load, and the generator is at . At , the load impedance is connected. The definition of impedance is , therefore at the z=0 end of the transmission line, the voltage and current on the transmission line at that point have to obey boundary condition that the load impedance imposes.
Substituting z=0, the boundary condition, in Equations eq:RCvtl-eq:RCctl, we get Equations eq:RCvtl1-eq:RCctl1.
Dividing the two above equations, we get the impedance at the load.
We can now solve the above equation for
Lowercase is called the ”normalized load impedance”. It is the actual impedance divided by the transmission line impedance . For example, if the load impedance is , and the transmission-line impedance is , then the normalized impedance is . Normalized impedance is a unitless quantity.
Example
- (a)
- 100 transmission line is terminated in a series connection of a 50 resistor and 10 pF capacitor. The frequency of operation is 100 MHz. Find the voltage reflection coefficient.
- (b)
- For purely reactive load , find the reflection coefficient.
Voltage and Current on a transmission line
Now that we related forward and reflected voltage on a transmission line with the reflection coefficient at the load, we can re-write the equations for the current and voltage on a transmission line as:
We see that if we know the length of the line, line type, the load impedance, and the transmission line impedance, we can calculate all variables above, except for . In the following chapters, we will derive the equation for the forward going voltage at the load, but first, we will look at little more at the various reflection coefficients on a transmission line.
Reflection coefficient anywhere on the line
Equations eq:RCvtl-eq:RCctl can be concisely written as
Where is the forward voltage anywhere on the line, is reflected voltage anywhere on the line, is the forward current anywhere on the line, and is the reflected current anywhere on the line.
We can then define a reflection coefficient anywhere on the line as
Since we already defined as the reflection coefficient at the load, we can now simplify the general reflection coefficient as
It is important to remember that we defined points between the generator and the load as the negative z-axis. If the line length is, for example, l m long, the generator is then at z=-l m, and the load at z=0. To find the reflection coefficient at some distance m away from the load, at m, the equation for the reflection coefficient will be
Since we already defined the reflection coefficient at the load, the reflection at any point on the line is
Reflection coefficient at the input of the transmission line
Using the reasoning above, the reflection coefficient at the input of the line whose length is is