Magnetic flux, review of electric flux
A conceptual definition of magnetic flux is the number of magnetic field lines penetrating a surface.
Mathematically, magnetic flux is defined through magnetic flux density vector B as
If the angle between the surface dS and B vector is the same, and the B vector is constant on the surface, we have that , or . Vector is called magnetic flux density, just like in electrostatics, vector was called electric flux density vector.
Magnetic flux density vector and magnetic field vector are related through the magnetic permeability of the material .
Similarly, in electrostatics, the electric flux density vector , and electric field vector are related through the electric permittivity of the material .
Definition of inductance
A simplified, conceptual definition of inductance is the number of magnetic field lines around a conductor, divided by the current in a wire.
For example, if we have five magnetic field lines around the wire that carries the current 1A, then the inductance is L=5/1=5 H. If we have another wire that makes ten magnetic field lines around it for the same current flowing through it of 1A, then the inductance of this wire is L=10 H. This type of inductance is called self-inductance. We will talk about mutual inductance in the section below.
The scientific definition of inductance is the ratio of magnetic flux to the current that produced it.
Magnetostatic energy
Inductors store magnetic energy. Capacitors store electric energy. The magnetic energy stored in an inductor is
The total magnetic energy stored in a volume is
B is the magnetic flux density, H is the magnetic field, and v is the volume in which the energy is stored.
By equating the above two equations, we can find the inductance of an inductor as
In linear, homegenous materials , the equation simplifies to
In the electrostatics section, we found that the capacitance is found as
V is the potential difference, v is the volume where electric energy is stored, and E is the electric field.
Deriving inductance for a coaxial cable
Derive the inductance of a length h of a coaxial cable carrying current I. The inner radius of the coaxial cable is a, and the outer radius is b.
- Solution:
- In the previous section, we derived the magnetic field around an
infinite straight line carrying current . The magnetic field between a coaxial
cable’s inner and outer conductor is the same as an infinite straight line’s
magnetic field.
Using the equation for the magnetic field and integrating throughout a section of the volume between the inner and outer conductor of the coaxial cable, we get
since the only variable is the distance r, and the unit volume in cylindrical coordinates is , the integral simplifies to
The final expression for the inductance of a coaxial cable is

Types of inductance
- (a)
- Internal self-inductance. The definition is the number of magnetic field lines inside a wire, divided by the current that flows through the same wire.
- (b)
- External self-inductance. The definition is the number of magnetic field lines outside of a wire, divided by the current that flows through the same wire.
- (c)
- Mutual inductance. The definition of this inductance is the number of magnetic field lines around one wire produced by the current flowing through another wire.
- (d)
- Partial inductance. This inductance is defined for a portion of a current or a wire because we do not know (or we are not interested in) how the current returns back to the source.
Self Inductance
A simple conceptual definition of self-inductance is the number of magnetic field lines around the wire, divided by the current in the same wire (that produced the magnetic field around the wire).
For example, if we have five magnetic field lines around the wire that carries the current 1A, then the inductance is L=5/1=5 H. If we have another wire that makes ten magnetic field lines around it for the same current flowing through it of 1A, then the inductance of this wire is L=10 H. This type of inductance is called (external) self-inductance.
Mutual Inductance
Mutual inductance is defined for two or more wires. It is defined as the number of magnetic field lines around one conductor, divided by the current produced through another conductor.
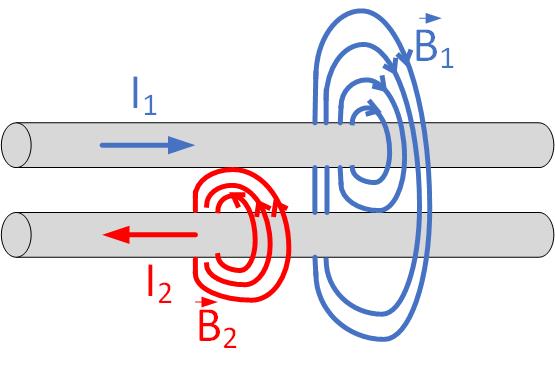
For example, in Figure MutualInduc2, we have two currents, and flowing in the same direction. Their magnetic fields, therefore, rotate in the same direction. Current produces four magnetic field lines, and current produces three magnetic field lines. Two of the magnetic field lines from conductor 1 encircle wire 2 as well. The total number of magnetic field lines around the second conductor is therefore 5. Two magnetic field lines from conductor 1, and three from conductor 2 itself is 2+3=5. Therefore mutual inductance is When the magnetic field from two wires is in the same direction, the fluxes add.
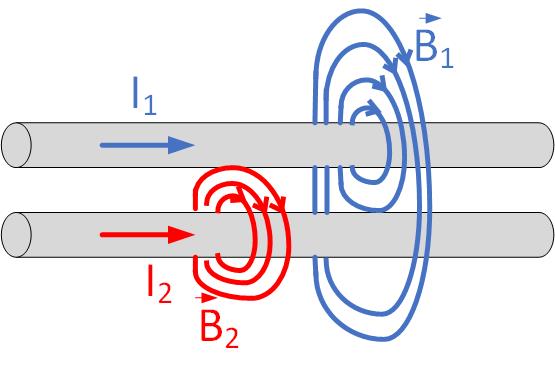
In another example, in Figure MutualInduc1, we have two currents, and flowing in the opposite directions. Current again produces four magnetic field lines, and current produces three magnetic field lines. Two of the magnetic field lines from conductor 1 encircle wire 2 as well. However, this time, the magnetic field lines flow in opposite directions. Therefore, the total number of magnetic field lines around conductor 2 is 3-2=1. Therefore mutual inductance is When the magnetic field from two wires is in the opposite direction, fluxes subtract.