This section aims to introduce two different ways we represent complex numbers: Cartesian coordinates, and Polar coordinates. We often use complex numbers in Cartesian coordinates when we discuss impedance or admittance. We often use complex numbers in polar coordinates to discuss magnitude and phase of voltages, currents, transfer functions, and Bode Plots. We can also represent sinusoidal signals with complex numbers with phasors. It is critically important that we understand this chapter.
In Equation cartesian, a complex number z is represented in rectangular coordinate system, where is the real part, is the imaginary part, and .
Equation polar, shows a complex number z in the polar coordinate system, where is the magnitude, and is the angle (aka phase) of the complex number.
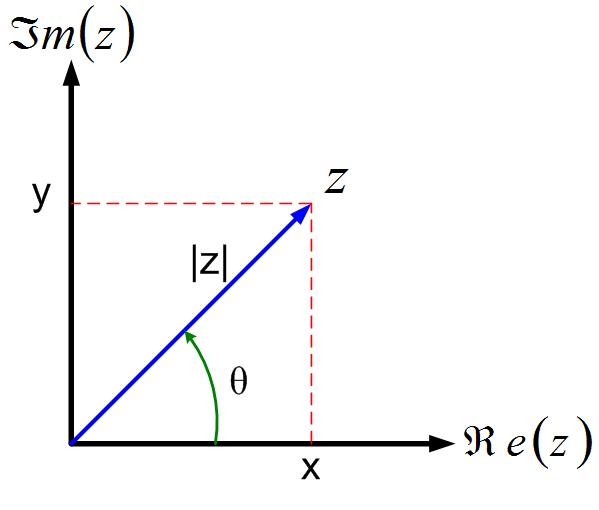
The geometric interpretation of these two equations is shown in Figure cartpol. The magnitude is the length of the triangle’s hypothenuse, and the angle is the angle that the hypothenuse makes with the x-axis.
In Figure cartpol, we represent a complex number with a ”position vector.” Position vectors are vectors that start at the center of the coordinate system and end at any point in the coordinate system. We see that phasor is a vector that represents a complex number in a polar coordinate system.
You may be wondering why we represent the phase of a complex number in the polar coordinate system as because in the circuits class, you used . Great question. That brings us to Euler’s formula that we will discuss in section Euler’s Formula.
Conversion between Cartesian and Polar coordinate systems
To find magnitude and angle when we know real and imaginary parts of a complex number, we use the Pythagorean Theorem to find the magnitude of the complex number as in Equation eq:polar_mag, and use the definition of the tangent to find the angle as in Equation eq:polar_angle.
To find the real and imaginary part of a complex number when we know magnitude and phase, we use trigonometry. To find the real part of the complex number as in Equation eq:cart_real, use the definition of cosine and sine to find the imaginary part of the complex number as in Equation eq:cart_imag.
Write magnitude and phase of complex number