Forward voltage on a transmission line

$\newenvironment {prompt}{}{} \newcommand {\ungraded }[0]{} \newcommand {\todo }[0]{} \newcommand {\oiint }[0]{{\large \bigcirc }\kern -1.56em\iint } \newcommand {\mooculus }[0]{\textsf {\textbf {MOOC}\textnormal {\textsf {ULUS}}}} \newcommand {\npnoround }[0]{\nprounddigits {-1}} \newcommand {\npnoroundexp }[0]{\nproundexpdigits {-1}} \newcommand {\npunitcommand }[1]{\ensuremath {\mathrm {#1}}} \newcommand {\RR }[0]{\mathbb R} \newcommand {\R }[0]{\mathbb R} \newcommand {\N }[0]{\mathbb N} \newcommand {\Z }[0]{\mathbb Z} \newcommand {\sagemath }[0]{\textsf {SageMath}} \newcommand {\d }[0]{\mathop {}\!d} \newcommand {\l }[0]{\ell } \newcommand {\ddx }[0]{\frac {d}{\d x}} \newcommand {\zeroOverZero }[0]{\ensuremath {\boldsymbol {\tfrac {0}{0}}}} \newcommand {\inftyOverInfty }[0]{\ensuremath {\boldsymbol {\tfrac {\infty }{\infty }}}} \newcommand {\zeroOverInfty }[0]{\ensuremath {\boldsymbol {\tfrac {0}{\infty }}}} \newcommand {\zeroTimesInfty }[0]{\ensuremath {\small \boldsymbol {0\cdot \infty }}} \newcommand {\inftyMinusInfty }[0]{\ensuremath {\small \boldsymbol {\infty -\infty }}} \newcommand {\oneToInfty }[0]{\ensuremath {\boldsymbol {1^\infty }}} \newcommand {\zeroToZero }[0]{\ensuremath {\boldsymbol {0^0}}} \newcommand {\inftyToZero }[0]{\ensuremath {\boldsymbol {\infty ^0}}} \newcommand {\numOverZero }[0]{\ensuremath {\boldsymbol {\tfrac {\#}{0}}}} \newcommand {\dfn }[0]{\textbf } \newcommand {\unit }[0]{\mathop {}\!\mathrm } \newcommand {\eval }[1]{\bigg [ #1 \bigg ]} \newcommand {\seq }[1]{\left ( #1 \right )} \newcommand {\epsilon }[0]{\varepsilon } \newcommand {\phi }[0]{\varphi } \newcommand {\iff }[0]{\Leftrightarrow } \DeclareMathOperator {\arccot }{arccot} \DeclareMathOperator {\arcsec }{arcsec} \DeclareMathOperator {\arccsc }{arccsc} \DeclareMathOperator {\si }{Si} \DeclareMathOperator {\scal }{scal} \DeclareMathOperator {\sign }{sign} \newcommand {\arrowvec }[1]{{\overset {\rightharpoonup }{#1}}} \newcommand {\vec }[1]{{\overset {\boldsymbol {\rightharpoonup }}{\mathbf {#1}}}\hspace {0in}} \newcommand {\point }[1]{\left (#1\right )} \newcommand {\pt }[1]{\mathbf {#1}} \newcommand {\Lim }[2]{\lim _{\point {#1} \to \point {#2}}} \DeclareMathOperator {\proj }{\mathbf {proj}} \newcommand {\veci }[0]{{\boldsymbol {\hat {\imath }}}} \newcommand {\vecj }[0]{{\boldsymbol {\hat {\jmath }}}} \newcommand {\veck }[0]{{\boldsymbol {\hat {k}}}} \newcommand {\vecl }[0]{\vec {\boldsymbol {\l }}} \newcommand {\uvec }[1]{\mathbf {\hat {#1}}} \newcommand {\utan }[0]{\mathbf {\hat {t}}} \newcommand {\unormal }[0]{\mathbf {\hat {n}}} \newcommand {\ubinormal }[0]{\mathbf {\hat {b}}} \newcommand {\dotp }[0]{\bullet } \newcommand {\cross }[0]{\boldsymbol \times } \newcommand {\grad }[0]{\boldsymbol \nabla } \newcommand {\divergence }[0]{\grad \dotp } \newcommand {\curl }[0]{\grad \cross } \newcommand {\lto }[0]{\mathop {\longrightarrow \,}\limits } \newcommand {\bar }[0]{\overline } \newcommand {\surfaceColor }[0]{violet} \newcommand {\surfaceColorTwo }[0]{redyellow} \newcommand {\sliceColor }[0]{greenyellow} \newcommand {\vector }[1]{\left \langle #1\right \rangle } \newcommand {\sectionOutcomes }[0]{} \newcommand {\HyperFirstAtBeginDocument }[0]{\AtBeginDocument }$

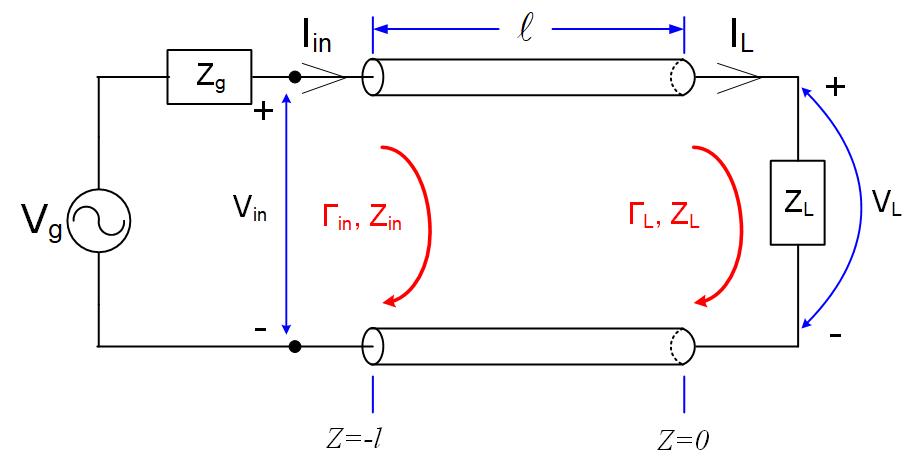
Again, we will look at a transmission line circuit in Figure fig:FVTRLine to find the input impedance on a transmission line.

Figure 1: Transmission Line connects generator and the load.

The equations for the voltage and current anywhere (any z) on a transmission line are

$\begin{eqnarray} \tilde{V}(z)= \tilde{V}_0^+ (e^{-j \beta z} - \Gamma_L e^{j \beta z } ) \label{eq:FVvtlfin} \\ I(z)= \frac{\tilde{V}_0^+}{Z_0} (e^{-j \beta z} - \Gamma_L e^{j \beta z} ) \label{eq:FVitlfin} \end{eqnarray}$

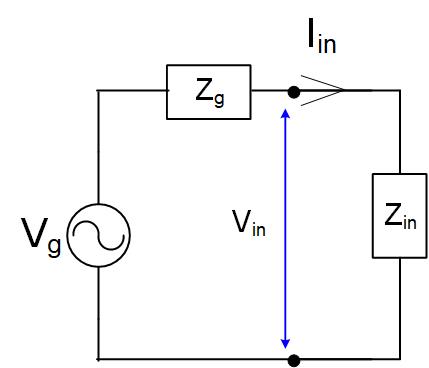
Using the equations from the previous section, we can replace the transmission line with its input impedance, Figure fig:FVTRLineEqCirc.

Figure 2: Transmission Line connects generator and the load.

Forward voltage phasor as a function of load impedance

From Figure fig:FVTRLineEqCirc, we can find the input voltage on a transmission line using the voltage divider.

$\begin{equation} \tilde{V}_{in}= \frac{Z_{in}}{Z_{in}+Z_g} \tilde{V}_g \end{equation}$

Using Equation eq:FVitlfin, we can also find the input voltage. The input voltage equation at the generator $z=-l$ is:

$\begin{eqnarray} \tilde{V}_{in}=\tilde{V}(z=-l)= \tilde{V}_0^+ (e^{j \beta l} + \Gamma_L e^{-j \beta l } ) \end{eqnarray}$

Since these two equations represent the same input voltage we can make them equal.

$\begin{equation} \tilde{V}_0^+ (e^{j \beta l} + \Gamma_L e^{-j \beta l }) = \frac{Z_{in}}{Z_{in}+Z_g} \tilde{V}_g \end{equation}$

Rearranging the equation, we find $\tilde {V}_0^+$ .

$\begin{eqnarray} \tilde{V}_0^+= \frac{\tilde{V}_g Z_{in}}{Z_g + Z_{in}} \frac{1}{e^{j \beta l} + \Gamma_L e^{-j \beta l}} \\ \end{eqnarray}$

Forward voltage phasor as a function of input reflection coefficient

There is another way to find the input impedance as a function of the input reflection coefficient.

We write KVL for the circuit in Figure fig:FVTRLineEqCirc.

$\begin{equation} \tilde{V}_g=Z_g \tilde{I}_{in} + \tilde{V}_{in} \label{eq:FVKVL} \end{equation}$

Using Equations eq:FVitlfin-eq:FVitlfin, we can also find the input voltage and current. Input voltage and current equation at the generator $z=-l$ are:

$\begin{eqnarray} \tilde{V}_{in}=\tilde{V}(z=-l)= \tilde{V}_0^+ (e^{j \beta l} + \Gamma_L e^{-j \beta l } ) \\ \tilde{I}_{in}=I(z=-l)= \frac{\tilde{V}_0^+}{Z_0} (e^{j \beta l} - \Gamma e^{-j \beta l} ) \end{eqnarray}$

Substituting these two equations in Equation eq:FVKVL we get

$\begin{equation} \tilde{V}_g=Z_g \frac{\tilde{V}_0^+}{Z_0} (e^{j \beta l} - \Gamma_L e^{-j \beta l} ) + \tilde{V}_0^+ (e^{j \beta l} + \Gamma_L e^{-j \beta l } ) \end{equation}$

We can re-write this equation as follows.

$\begin{equation} \tilde{V}_g=Z_g e^{j \beta l} \frac{\tilde{V}_0^+}{Z_0} (1 - \Gamma_L e^{-2j \beta l} ) + \tilde{V}_0^+ e^{j \beta l} (1 + \Gamma_L e^{-2j \beta l } ) \end{equation}$

Using that $\Gamma _{in} = \Gamma _L e^{-2 j \beta l}$ is the input reflection coefficient, and multiplying through with $Z_0$ .

$\begin{equation} \tilde{V}_g Z_0=Z_g e^{j \beta l} \frac{\tilde{V}_0^+}{1} (1 - \Gamma_{in} ) + \tilde{V}_0^+ Z_0 e^{j \beta l} (1 + \Gamma_{in}) \end{equation}$

Rearranging the equation, we get $\tilde {V}_0^+$

$\begin{equation} \tilde{V}_0^+=\tilde{V}_g e^{-j \beta l} \frac{Z_0}{Z_0 (1+\Gamma_{in}) +Z_g (1-\Gamma_{in})} \end{equation}$

$\Gamma _{in} = \Gamma _L e^{-2 j \beta l}$ is the input reflection coefficient.

Special case - forward voltage when the generator and transmission-line impedance are equal

Because the generator’s impedance is equal to the transmission line impedance, we will use the second equation. When $Z_g=Z_0$ we see that the denominator simplifies into $Z_0 (1+\Gamma _{in}) +Z_g (1-\Gamma _{in}) = Z_0 (1+\Gamma _{in}+1-\Gamma _{in})=2$ , and we can further simplify the fraction to get the final value of $\tilde {V}_0^+=\frac {V_g}{2} e^{-j \beta l}$ .