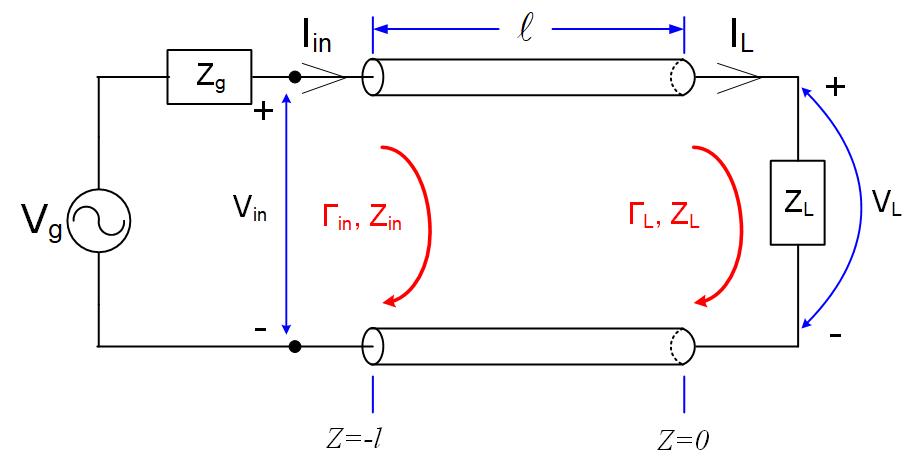
Again, we will look at a transmission line circuit in Figure fig:IITRLine to find the input impedance on a transmission line.
The equations for the voltage and current anywhere (any z) on a transmission line are
The voltage and current equations at the generator are:
Input impedance as a function of reflection coefficient
The input impedance is defined as . Since the line length is , the input impedance is
If we cancel common terms, we get
Now we can take in front of parenthesis from both numerator and denominator and then cancel it.
We have previously defined the reflection coefficient at the transmission line’s input as . The final equation for the input impedance is therefore
Input impedance as a function of load impedance
If we now look back at the Equation eq:theSecondway, here we can also use Euler’s formula , and the equation for the reflection coefficient at the load we find the input impedance of the line as shown below.
This equation will be soon become obsolete when we learn how to use the Smith Chart.
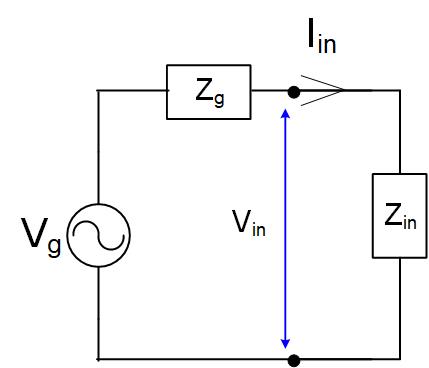
When we find the input impedance, we can replace the transmission line and the load, as shown in Figure fig:IITRLineEqCirc. In the next section, we will use input impedance to find the forward going voltage on a transmission line.