Example Transmission Line Problem

$\newenvironment {prompt}{}{} \newcommand {\ungraded }[0]{} \newcommand {\todo }[0]{} \newcommand {\oiint }[0]{{\large \bigcirc }\kern -1.56em\iint } \newcommand {\mooculus }[0]{\textsf {\textbf {MOOC}\textnormal {\textsf {ULUS}}}} \newcommand {\npnoround }[0]{\nprounddigits {-1}} \newcommand {\npnoroundexp }[0]{\nproundexpdigits {-1}} \newcommand {\npunitcommand }[1]{\ensuremath {\mathrm {#1}}} \newcommand {\RR }[0]{\mathbb R} \newcommand {\R }[0]{\mathbb R} \newcommand {\N }[0]{\mathbb N} \newcommand {\Z }[0]{\mathbb Z} \newcommand {\sagemath }[0]{\textsf {SageMath}} \newcommand {\d }[0]{\mathop {}\!d} \newcommand {\l }[0]{\ell } \newcommand {\ddx }[0]{\frac {d}{\d x}} \newcommand {\zeroOverZero }[0]{\ensuremath {\boldsymbol {\tfrac {0}{0}}}} \newcommand {\inftyOverInfty }[0]{\ensuremath {\boldsymbol {\tfrac {\infty }{\infty }}}} \newcommand {\zeroOverInfty }[0]{\ensuremath {\boldsymbol {\tfrac {0}{\infty }}}} \newcommand {\zeroTimesInfty }[0]{\ensuremath {\small \boldsymbol {0\cdot \infty }}} \newcommand {\inftyMinusInfty }[0]{\ensuremath {\small \boldsymbol {\infty -\infty }}} \newcommand {\oneToInfty }[0]{\ensuremath {\boldsymbol {1^\infty }}} \newcommand {\zeroToZero }[0]{\ensuremath {\boldsymbol {0^0}}} \newcommand {\inftyToZero }[0]{\ensuremath {\boldsymbol {\infty ^0}}} \newcommand {\numOverZero }[0]{\ensuremath {\boldsymbol {\tfrac {\#}{0}}}} \newcommand {\dfn }[0]{\textbf } \newcommand {\unit }[0]{\mathop {}\!\mathrm } \newcommand {\eval }[1]{\bigg [ #1 \bigg ]} \newcommand {\seq }[1]{\left ( #1 \right )} \newcommand {\epsilon }[0]{\varepsilon } \newcommand {\phi }[0]{\varphi } \newcommand {\iff }[0]{\Leftrightarrow } \DeclareMathOperator {\arccot }{arccot} \DeclareMathOperator {\arcsec }{arcsec} \DeclareMathOperator {\arccsc }{arccsc} \DeclareMathOperator {\si }{Si} \DeclareMathOperator {\scal }{scal} \DeclareMathOperator {\sign }{sign} \newcommand {\arrowvec }[1]{{\overset {\rightharpoonup }{#1}}} \newcommand {\vec }[1]{{\overset {\boldsymbol {\rightharpoonup }}{\mathbf {#1}}}\hspace {0in}} \newcommand {\point }[1]{\left (#1\right )} \newcommand {\pt }[1]{\mathbf {#1}} \newcommand {\Lim }[2]{\lim _{\point {#1} \to \point {#2}}} \DeclareMathOperator {\proj }{\mathbf {proj}} \newcommand {\veci }[0]{{\boldsymbol {\hat {\imath }}}} \newcommand {\vecj }[0]{{\boldsymbol {\hat {\jmath }}}} \newcommand {\veck }[0]{{\boldsymbol {\hat {k}}}} \newcommand {\vecl }[0]{\vec {\boldsymbol {\l }}} \newcommand {\uvec }[1]{\mathbf {\hat {#1}}} \newcommand {\utan }[0]{\mathbf {\hat {t}}} \newcommand {\unormal }[0]{\mathbf {\hat {n}}} \newcommand {\ubinormal }[0]{\mathbf {\hat {b}}} \newcommand {\dotp }[0]{\bullet } \newcommand {\cross }[0]{\boldsymbol \times } \newcommand {\grad }[0]{\boldsymbol \nabla } \newcommand {\divergence }[0]{\grad \dotp } \newcommand {\curl }[0]{\grad \cross } \newcommand {\lto }[0]{\mathop {\longrightarrow \,}\limits } \newcommand {\bar }[0]{\overline } \newcommand {\surfaceColor }[0]{violet} \newcommand {\surfaceColorTwo }[0]{redyellow} \newcommand {\sliceColor }[0]{greenyellow} \newcommand {\vector }[1]{\left \langle #1\right \rangle } \newcommand {\sectionOutcomes }[0]{} \newcommand {\HyperFirstAtBeginDocument }[0]{\AtBeginDocument }$

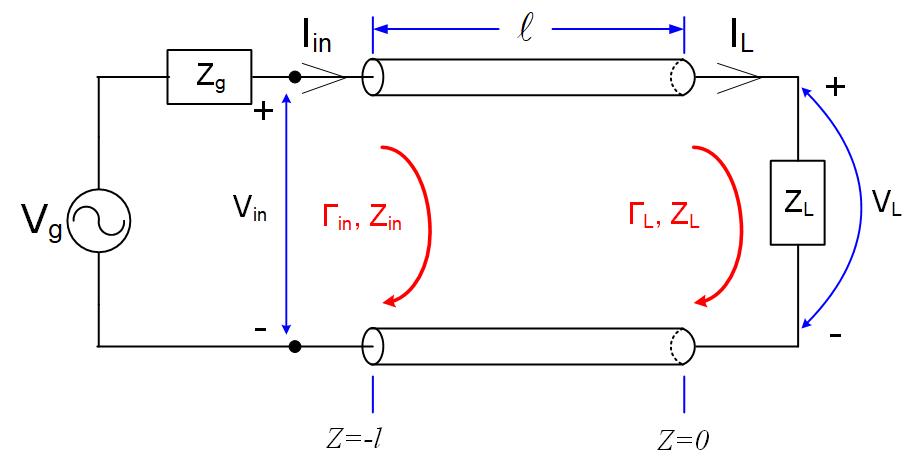
A transmitter operated at 20MHz, Vg=100V with $Z_g=50 \Omega$ internal impedance is connected to an antenna load through l=6.33m of the line. The line is a lossless $Z_0=50 \Omega$ , $\beta =0.595rad/m$ . The antenna impedance at 20MHz measures $Z_L=36+j20 \Omega$ . Set the beginning of the z-axis at the load, as shown in Figure fig:TRLine.

(a): What is the electrical length of the line?
(b): What is the input impedance of the line $Z_{in}$ ?
(c): What is the forward going voltage at the load $\tilde {V}_0^+$ ?
(d): Find the expression for forward voltage anywhere on the line.
(e): Find the expression for reflected voltage anywhere on the line.
(f): Find the total voltage anywhere on the line.
(g): Find the expression for forward current anywhere on the line.
(h): Find the expression for reflected current anywhere on the line.
(i): Find the total current anywhere on the line.
(j): Instead of the antenna, a load impedance $Z_l=50 \Omega$ is connected to this 50 Ohm line. How will that change the equations above?

Figure 1: Transmission Line connects generator and the load.

The equations for the voltage and current anywhere (any z) on a transmission line are

$\begin{eqnarray} \tilde{V}(z)= \tilde{V}_0^+ (e^{-j \beta z} + |\Gamma| e^{j \beta z + \Theta_r} ) \label{eq:vtlfin} \\ I(z)= \frac{\tilde{V}_0^+}{Z_0} (e^{-j \beta z} - \Gamma e^{j \beta z} ) \label{eq:itlfin} \end{eqnarray}$

We are given phase constant $\beta$ , and we have to find the other unknowns: phasor of voltage at the load $\tilde {V}_0^+$ , and the reflection coefficient $\Gamma$ .

Since we know the load impedance $Z_L$ , and the transmission-line impedance $Z_0$ , we can find the reflection coefficient $\Gamma$ using Equation eq:reflcoe1.

$\begin{eqnarray} \Gamma = \frac{Z_L -Z_0}{Z_L +Z_0}=0.279 \, e^{j112^o}=0.279 \, e^{j1.95 \unit{rad}} \label{eq:reflcoe1} \end{eqnarray}$

To find the input impedance of the line, we use the equation

$\begin{eqnarray} Z_{in}= Z_0 \frac{Z_L+ j Z_0 \tan \beta l}{Z_0+ j Z_L \tan \beta l} = 70.8+ j 27.1 \Omega \end{eqnarray}$

We can use one of the following two equations to find the forward going voltage at the load:

$\begin{eqnarray} \tilde{V}_0^+= \frac{\tilde{V}_g Z_{in}}{Z_g + Z_{in}} \frac{1}{e^{j \beta l} + \Gamma e^{-j \beta l}} \\ \tilde{V}_0^+=V_g e^{-j \beta l} \frac{Z_0}{Z_0 (1+\Gamma_{in}) +Z_g (1-\Gamma_{in})} \end{eqnarray}$

Because the generator’s impedance is equal to the transmission line impedance, we will use the second equation. When $Z_g=Z_0$ we see that the denominator simplifies into $Z_0 (1+\Gamma _{in}) +Z_g (1-\Gamma _{in}) = Z_0 (1+\Gamma _{in}+1-\Gamma _{in})$ and we can further simplify the fraction to get the final value of $\tilde {V}_0^+=\frac {V_g}{2} e^{-j \beta l}$ . Since $\beta l = \frac {2 \pi }{\lambda } \, 0.6 \lambda$ , the forward going voltage at the load is $\tilde {V}_0^+=50 \, e^{-j1.2 \pi } = 50 \, e^{-j3.768} =50 \, e^{-j216^o}$ .

The equations of the voltage and current anywhere on the line are therefore

$\begin{eqnarray} \tilde{V}(z)= 50 e^{-j3.768} (e^{-j 0.595 z} + 0.279 e^{j 0.595 z + 1.95} ) \\ I(z)= e^{-j3.768} (e^{-j 0.595 z} - 0.279 e^{j 0.595 z+ 1.95} ) \end{eqnarray}$

Suppose we replace the antenna with another load of impedance $50\Omega$ . In that case, the reflection coefficient from the load will be zero, and the reflected voltages will disappear, so the voltage and current will be equal to the forward-going voltage on the transmission line.

$\begin{eqnarray} \tilde{V}(z)= \tilde{V}_0^+ e^{-j \beta z} \\ I(z)= \frac{\tilde{V}_0^+}{Z_0} e^{-j \beta z} \end{eqnarray}$