Mixed Impedance Matching

$\newenvironment {prompt}{}{} \newcommand {\ungraded }[0]{} \newcommand {\todo }[0]{} \newcommand {\oiint }[0]{{\large \bigcirc }\kern -1.56em\iint } \newcommand {\mooculus }[0]{\textsf {\textbf {MOOC}\textnormal {\textsf {ULUS}}}} \newcommand {\npnoround }[0]{\nprounddigits {-1}} \newcommand {\npnoroundexp }[0]{\nproundexpdigits {-1}} \newcommand {\npunitcommand }[1]{\ensuremath {\mathrm {#1}}} \newcommand {\RR }[0]{\mathbb R} \newcommand {\R }[0]{\mathbb R} \newcommand {\N }[0]{\mathbb N} \newcommand {\Z }[0]{\mathbb Z} \newcommand {\sagemath }[0]{\textsf {SageMath}} \newcommand {\d }[0]{\mathop {}\!d} \newcommand {\l }[0]{\ell } \newcommand {\ddx }[0]{\frac {d}{\d x}} \newcommand {\zeroOverZero }[0]{\ensuremath {\boldsymbol {\tfrac {0}{0}}}} \newcommand {\inftyOverInfty }[0]{\ensuremath {\boldsymbol {\tfrac {\infty }{\infty }}}} \newcommand {\zeroOverInfty }[0]{\ensuremath {\boldsymbol {\tfrac {0}{\infty }}}} \newcommand {\zeroTimesInfty }[0]{\ensuremath {\small \boldsymbol {0\cdot \infty }}} \newcommand {\inftyMinusInfty }[0]{\ensuremath {\small \boldsymbol {\infty -\infty }}} \newcommand {\oneToInfty }[0]{\ensuremath {\boldsymbol {1^\infty }}} \newcommand {\zeroToZero }[0]{\ensuremath {\boldsymbol {0^0}}} \newcommand {\inftyToZero }[0]{\ensuremath {\boldsymbol {\infty ^0}}} \newcommand {\numOverZero }[0]{\ensuremath {\boldsymbol {\tfrac {\#}{0}}}} \newcommand {\dfn }[0]{\textbf } \newcommand {\unit }[0]{\mathop {}\!\mathrm } \newcommand {\eval }[1]{\bigg [ #1 \bigg ]} \newcommand {\seq }[1]{\left ( #1 \right )} \newcommand {\epsilon }[0]{\varepsilon } \newcommand {\phi }[0]{\varphi } \newcommand {\iff }[0]{\Leftrightarrow } \DeclareMathOperator {\arccot }{arccot} \DeclareMathOperator {\arcsec }{arcsec} \DeclareMathOperator {\arccsc }{arccsc} \DeclareMathOperator {\si }{Si} \DeclareMathOperator {\scal }{scal} \DeclareMathOperator {\sign }{sign} \newcommand {\arrowvec }[1]{{\overset {\rightharpoonup }{#1}}} \newcommand {\vec }[1]{{\overset {\boldsymbol {\rightharpoonup }}{\mathbf {#1}}}\hspace {0in}} \newcommand {\point }[1]{\left (#1\right )} \newcommand {\pt }[1]{\mathbf {#1}} \newcommand {\Lim }[2]{\lim _{\point {#1} \to \point {#2}}} \DeclareMathOperator {\proj }{\mathbf {proj}} \newcommand {\veci }[0]{{\boldsymbol {\hat {\imath }}}} \newcommand {\vecj }[0]{{\boldsymbol {\hat {\jmath }}}} \newcommand {\veck }[0]{{\boldsymbol {\hat {k}}}} \newcommand {\vecl }[0]{\vec {\boldsymbol {\l }}} \newcommand {\uvec }[1]{\mathbf {\hat {#1}}} \newcommand {\utan }[0]{\mathbf {\hat {t}}} \newcommand {\unormal }[0]{\mathbf {\hat {n}}} \newcommand {\ubinormal }[0]{\mathbf {\hat {b}}} \newcommand {\dotp }[0]{\bullet } \newcommand {\cross }[0]{\boldsymbol \times } \newcommand {\grad }[0]{\boldsymbol \nabla } \newcommand {\divergence }[0]{\grad \dotp } \newcommand {\curl }[0]{\grad \cross } \newcommand {\lto }[0]{\mathop {\longrightarrow \,}\limits } \newcommand {\bar }[0]{\overline } \newcommand {\surfaceColor }[0]{violet} \newcommand {\surfaceColorTwo }[0]{redyellow} \newcommand {\sliceColor }[0]{greenyellow} \newcommand {\vector }[1]{\left \langle #1\right \rangle } \newcommand {\sectionOutcomes }[0]{} \newcommand {\HyperFirstAtBeginDocument }[0]{\AtBeginDocument }$

The real part of the load impedance is rarely equal to the transmission-line impedance. In most cases, we have to transform the real part of the impedance as well.

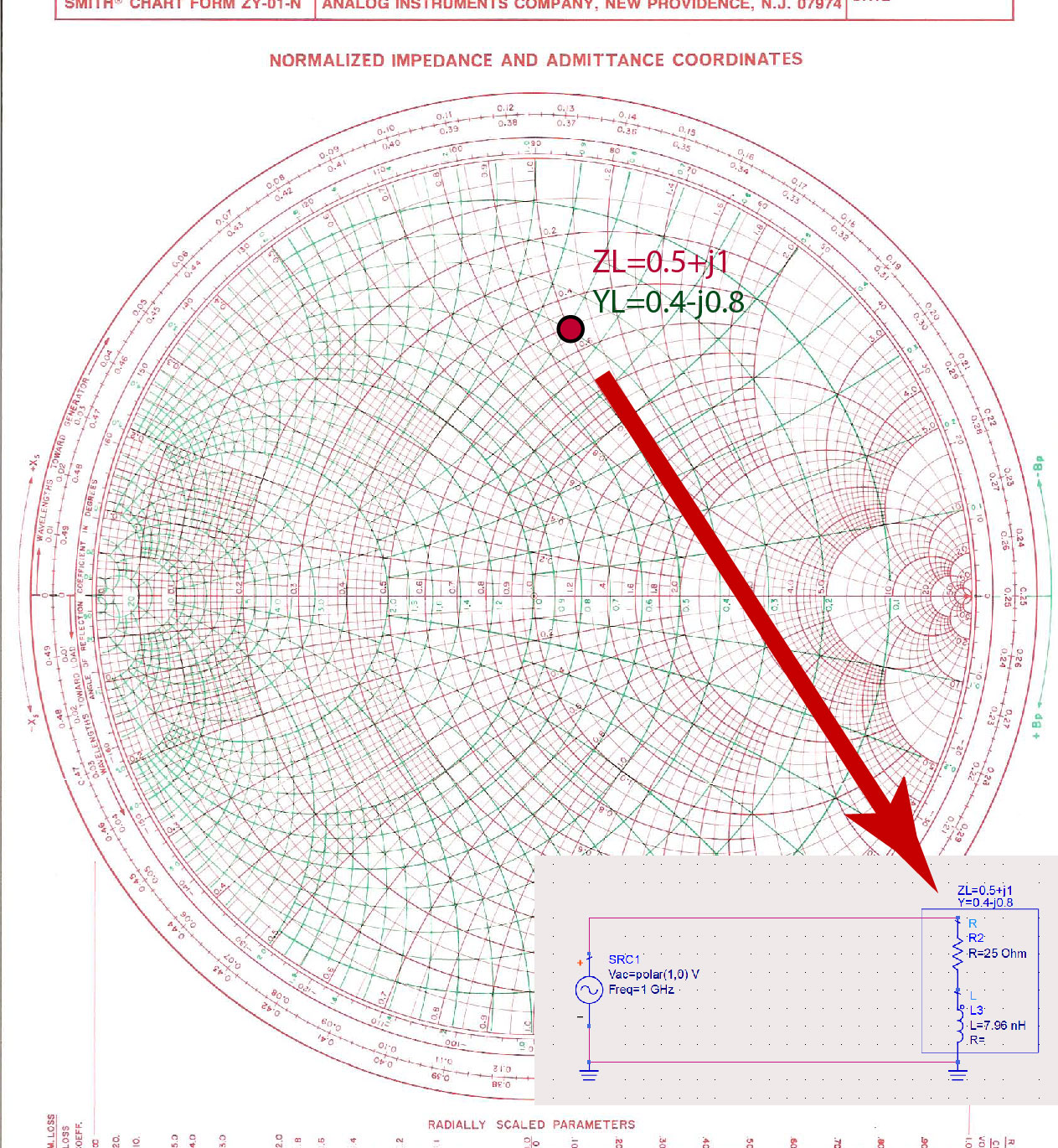
For example, load impedance $Z_L=25+j 50 \Omega$ represents a series connection of a $25\Omega$ resistor and a $7.96$ nH inductor at 1 GHz. To match $Z_L=25+j 50 \Omega$ impedance to the transmission-line impedance $Z_0=50 \Omega$ , we first normalize the load impedance to transmission-line impedance.

$\begin{equation} \bar{Z}_L=\frac{Z_L}{Z_0}=0.5+j1 \end{equation}$

This impedance is shown in Figure fig:PointSC.

Figure 1: Load impedance $Z_L=0.5+j1$ on Smith Chart.

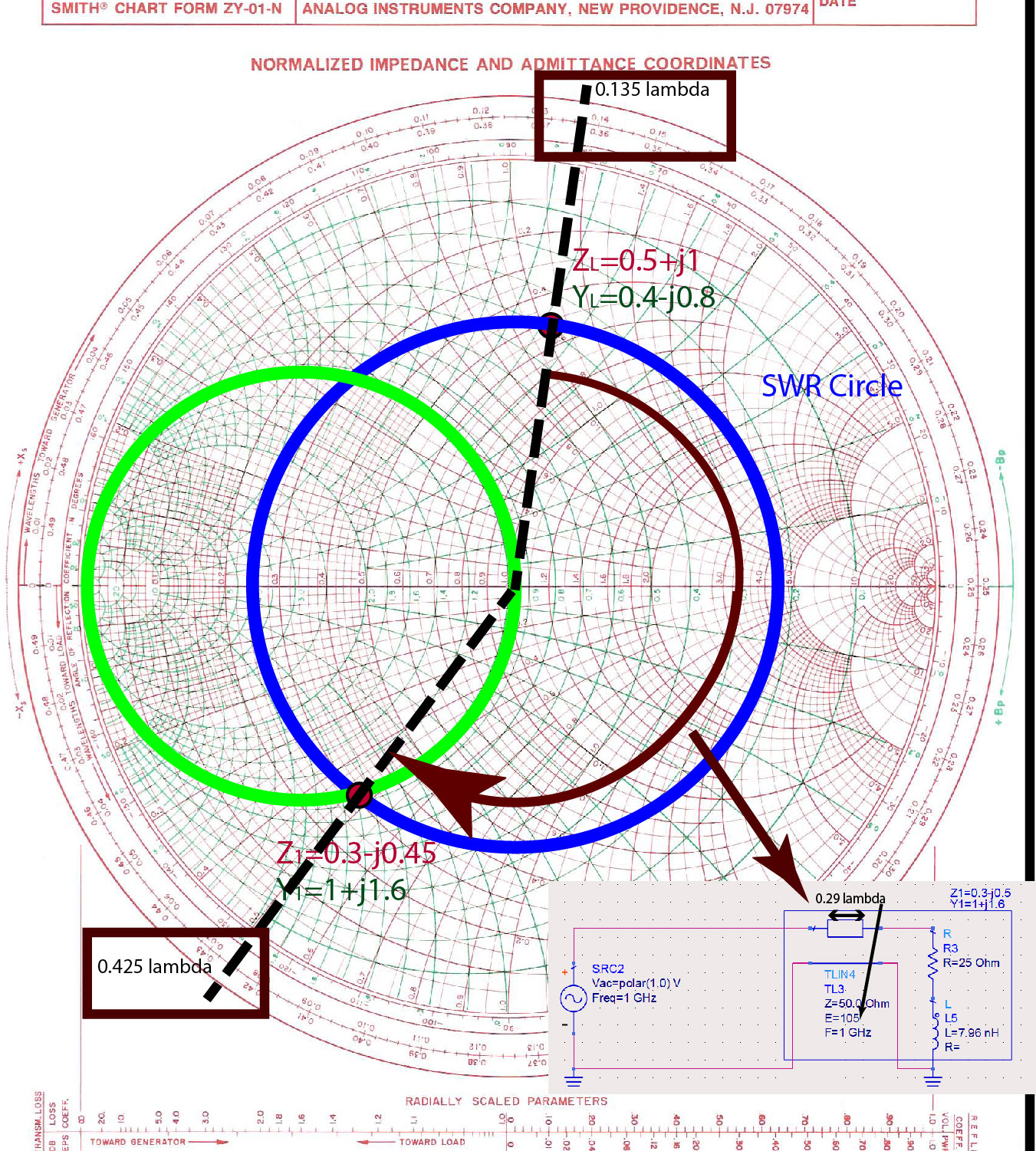
SWR circle

Then, we identify an SWR circle that this impedance is on, as shown in Figure fig:SWRfor25Ohm. The point where the SWR circle intersects the green circle is of interest because the real part of the input admittance is equal to one $Y_1=1$ . This second point, where $Y=1+j1.6$ , will give us the length of the line that we have to add to the load impedance.

Explain how the position of the load impedance on the Smith Chart changes the SWR circle.

To see how SWR circle changes depending on where the load impedance is use the following simulation. Click on point A, to change its position. Observe how SWR circle changes.

Length of the line that will transform the real part of load impedance

To find the length of the line that will transform the real part of $z_L$ to $y_{1}=1$ , we identify the position of the load impedance $Z_L=0.5+j1$ , and the input impedance $Z_1=0.3-j0.45$ at the Wavelengths Towards Generator (WTG) scale. The reason we picked impedance $Z_1=0.3-j0.45$ is because the real part of the admittance $y_1=1/z_1$ is equal to one $\Re (y_{1})=1$ . Load impedance $Z_L$ is at $0.135 \lambda$ , and the input impedance $Z_1$ is at $0.425 \lambda$ . The difference between these two positions gives us the length of the line $0.29 \lambda$ . In electrical degrees, this length is approximately $105^0$ . The input admittance to the line is now $Y_L=1+1.6$ .

Figure 2: SWR circle for impedance $Z_L=0.5+j1$ .

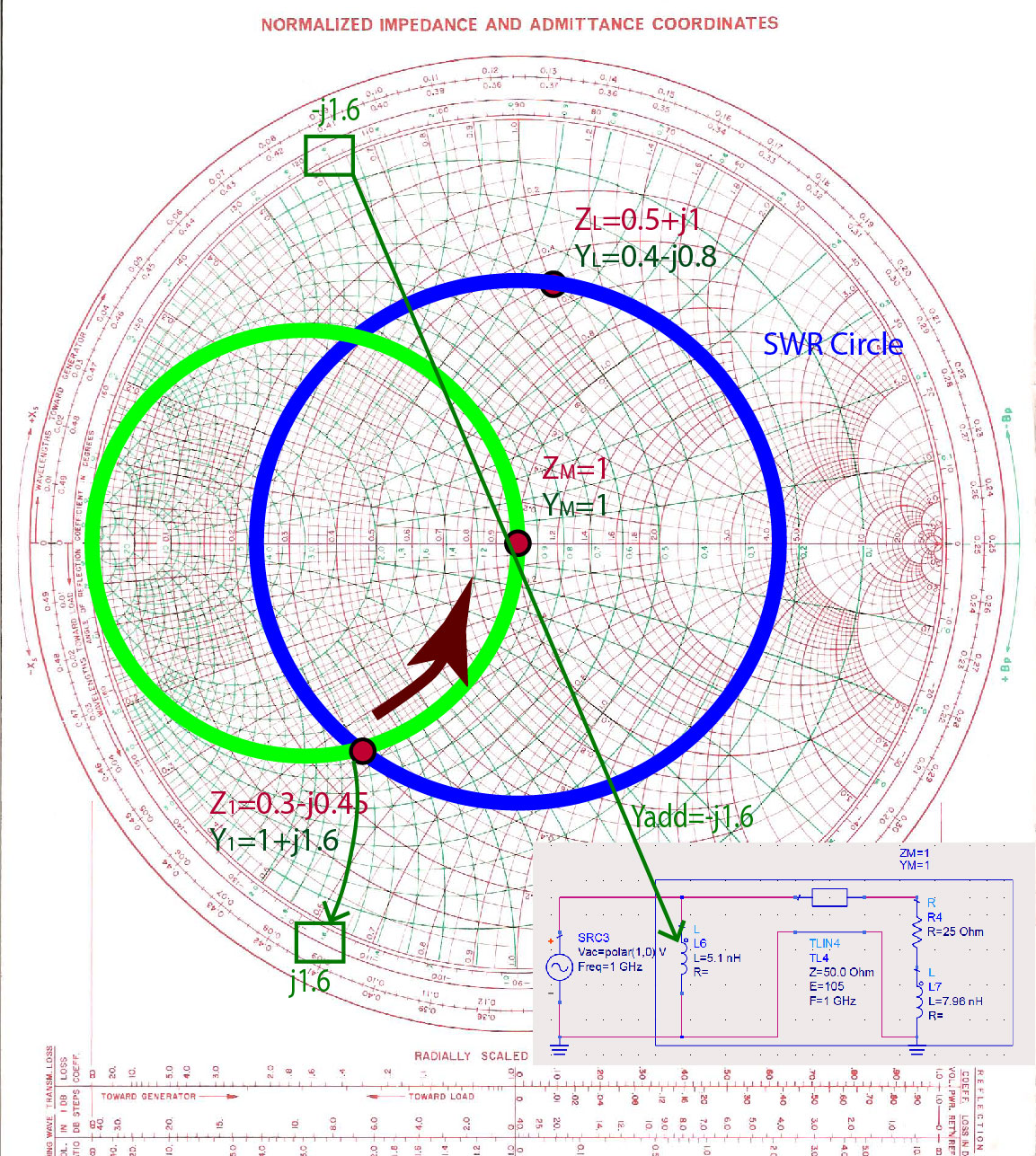
Adding a lumped-element to remove the susceptance

The final step is to add a susceptance that will remove the imaginary part of the input admittance $Y_1=1+j 1.6$ . We see that to get the final admittance of $Y_M=1$ , numerically, we have to add an admittance of $Y_{add}=-j1.6$ . This represents an inductance. Since we are adding the two admittances $Y_1+Y_{add}$ , they have to be in parallel (as we know that when elements are in parallel, we add their admittances).

Figure 3: The result of impedance matching.

SWR circle

Length of the line that will transform the real part of load impedance

Adding a lumped-element to remove the susceptance

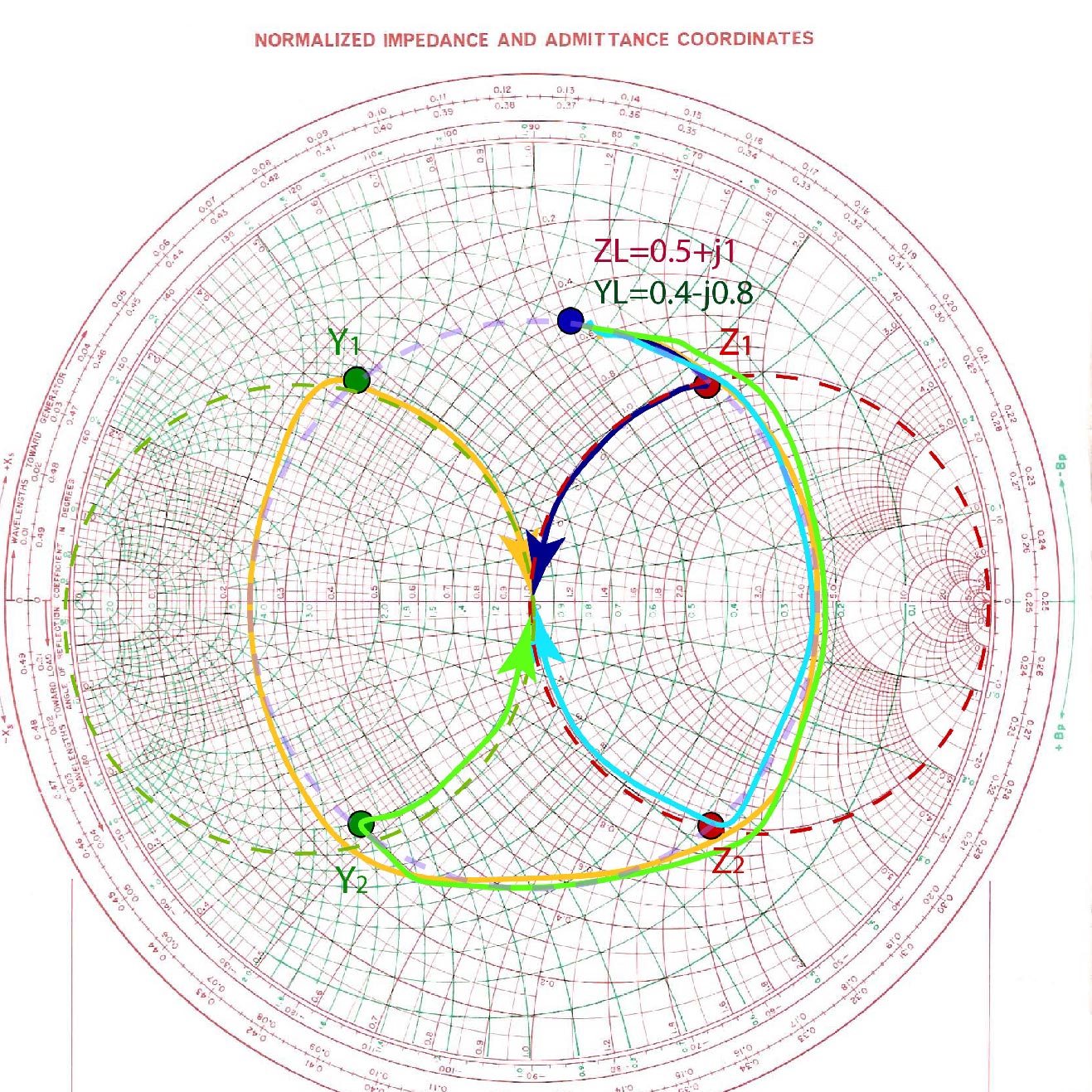
Other possible solutions