More about the Electrical force and field
We talked about the Electric Force in the previous section. To find the force on one charge, we had to know the position of all charges and what is their charge. To introduce Electric Field, we’ll call charge the source of the force and charge the charge that feels the force. Charge one produces the force, and charge two feels the force.
By introducing the concept of the field, we can separate the cause of the field and the effect that the field has on other charges. We can find a field due to a charge or charge distribution, and once we know this field, we don’t have to keep track of the source charge. We can just find the field’s effect on other charges or charge distributions.
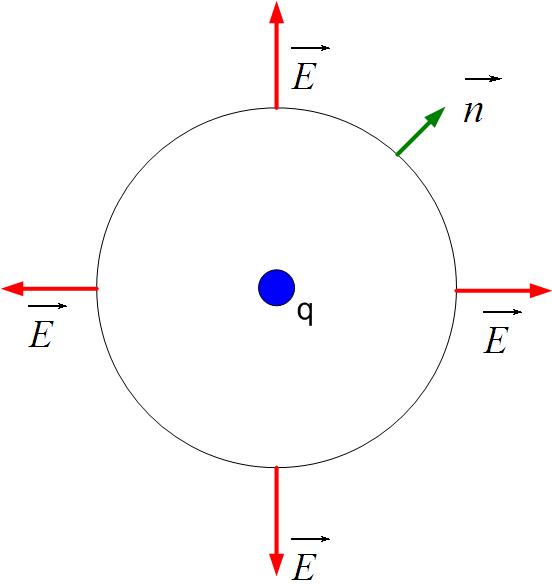
In the Equation forceField1 and are charges, r is the distance between the two charges, and is the unit vector directed from charge one to charge two. The electric field of a source charge is defined as the force that a charge would impress on a positive charge , divided by the amount of charge , as shown in Equation definitionOfField. One thing to remember is that in the definition of the electric field, we always assume that the charge is positive! This way, we remove the ambiguity of the field direction. The direction of the electric field at a point P from charge is always in the direction of the force that would act on a positive charge placed at that point, as shown in Figure UnitCh1.
If you carefully look at the Equation electricfield, you see that the electric field depends only on the source charge .
If the electric charge is in a medium other than air, the electric field becomes
We added a unitless quantity, , called the relative dielectric constant, or relative permittivity, of a material. values for different materials can be found online. For example, you can see its values for different materials here https://en.wikipedia.org/wiki/Relative_permittivity.
positive charge that is in an electric field experiences a force that is
Principle of Superposition
What is the electric field if we have more than one charge?
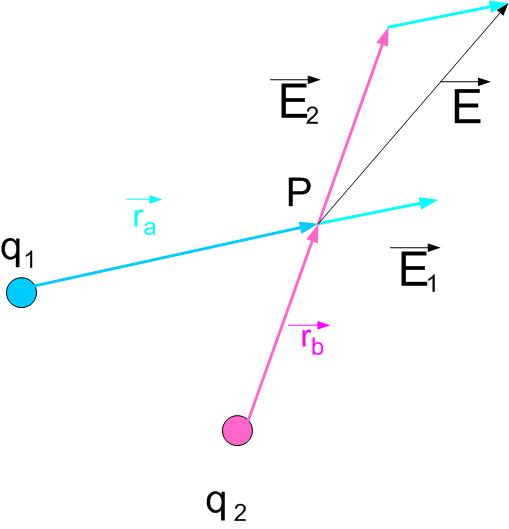
The total electric field at a point in space from the two charges is equal to the sum of the electric fields from the individual charges at that point.
If we have two charges, the total field due to both charges is equal to the vector sum of the fields due to individual charges, see Figure superposition. The field at
The fields or charges and are:
Where and are unit vectors in the direction of and . The total field due to both charges is
Electric Field in Rectangular Coordinates
The general equation for the electric field is given as
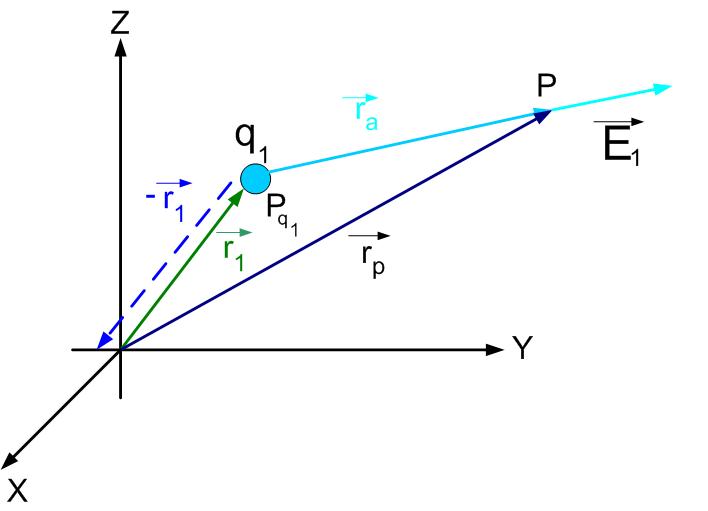
The electric field at a point due to a charge positioned at a point in the rectangular coordinate system is shown in Figure singlecharge1. The position vector of the point is
The position vector of point is equal to
The two vectors mark the beginning and the end of the distance vector between points and . The vector is the sum of vectors and
When we substitute position vectors and :
Vector has the magnitude of:
Unit vector in the direction of vector is:
Where is the distance between the charge and the point . Substituting expressions for , and in equation genfield we get
Substituting
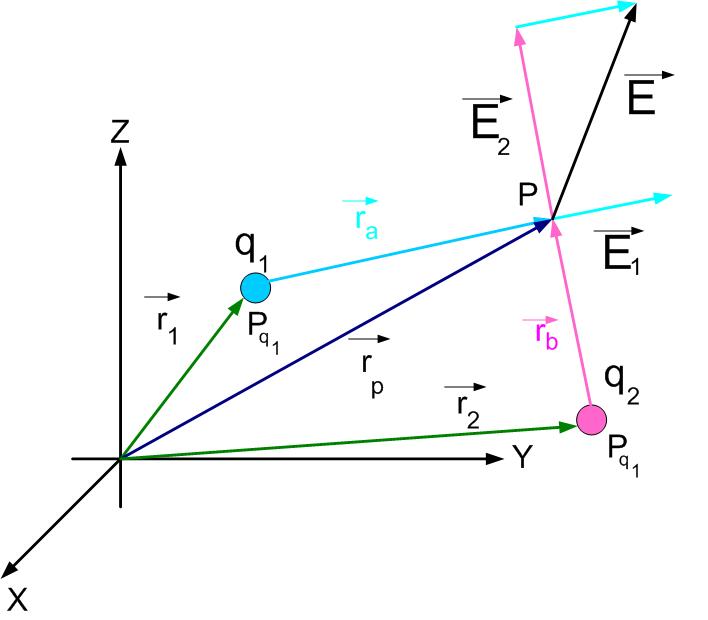
For two charges, as shown in Figure twocharges equation eqonecharge becomes