Because every function is a process that converts a collection of inputs to a corresponding collection of outputs, a natural question is: for a particular function, can we find a function that “undoes” the first functions? That is, given an output of the function, can we determine the input? If we phrase this question algebraically, it is analogous to asking: given an equation that defines is a function of , is it possible to find a corresponding equation where is a function of ?

Inverse functions

Let’s think about the problem in a more concrete way. Consider a situation in which Jessica is running a candle company. Say she starts the day with $15, but makes $4 for every candle she sells. A linear function representing the amount of money in dollars she has after selling candles is given by . To find out how much money she has after selling 20 candles, we can plug in 20 to the equation above:

Now suppose that Jessica tells us that at the end of the day, she ended up with $135. Would it be possible to figure out how many candles she sold? This type of “inverse question” is common in math. Notice that above, when we started with an amount of candles and wanted to find an amount of money, we first multiplied by 4, then added 15. Now, since we’re starting with an amount of money, we need to undo the processes we did before: first we subtract 15, and then divide by 4. We can represent this process by a function , which represents the number of candles sold if Jessica has dollars:

When we plug in $135 to this function, we find that Jessica has sold candles.

Let be a function defined by . Let be a function defined by .
a.
Recall that . What is ?
b.
Recall that . What is ?

After plugging in, we see that when we plug 20 into , we get , and when we plug 95 into (that is, we plug into ), we get back 20. Similarly, when we plug in the value into , we get back 135. The following diagram illustrates the situation:

In the above exploration, and are examples of inverse functions.

Note particularly what the equation says: for any input , the function will reverse the process of (which converts to ) because converts back to .

When a given function has a corresponding inverse function , we usually rename as , which we read aloud as “-inverse”. The equation now reads as , which we interpret as saying “-inverse converts back to ”. We similarly write that .

Dolbear’s function is used to model the number of snowy tree cricket chirps per minute to a corresponding Fahrenheit temperature.
a.
Solve the equation for in terms of . Call the resulting function .
b.
Explain in words the process or effect of the function . What does it take as input? What does it generate as output?
c.
Use the function that you found above to compute . Simplify your result as much as possible. Do likewise for . What do you notice about these two functions and ?
d.
Consider the equations and . Do these equations express different relationships between and , or do they express the same relationship in two different ways? Explain.

When a given function has an inverse function, it allows us to express the same relationship from two different points of view. For instance, if , we can show that the function reverses the effect of (and vice versa), and thus . We observe that are equivalent forms of the same equation, and thus they say the same thing from two different perspectives. The first version of the equation is solved for in terms of , while the second equation is solved for in terms of . This important principle holds in general whenever a function has an inverse function.

If has an inverse function, then the equations say the exact same thing but from two different perspectives.

When can we find inverses?

It’s important to note in the above definition of inverse functions that we say “If there exists ”. That is, we don’t guarantee that an inverse function exists for a given function. Thus, we might ask: how can we determine whether or not a given function has a corresponding inverse function? As with many questions about functions, there are often many different possible ways to explore such a question. Let’s consider this question through an arrow diagram, a table, a graph, and an algebraic formula.

Consider the following arrow diagrams.

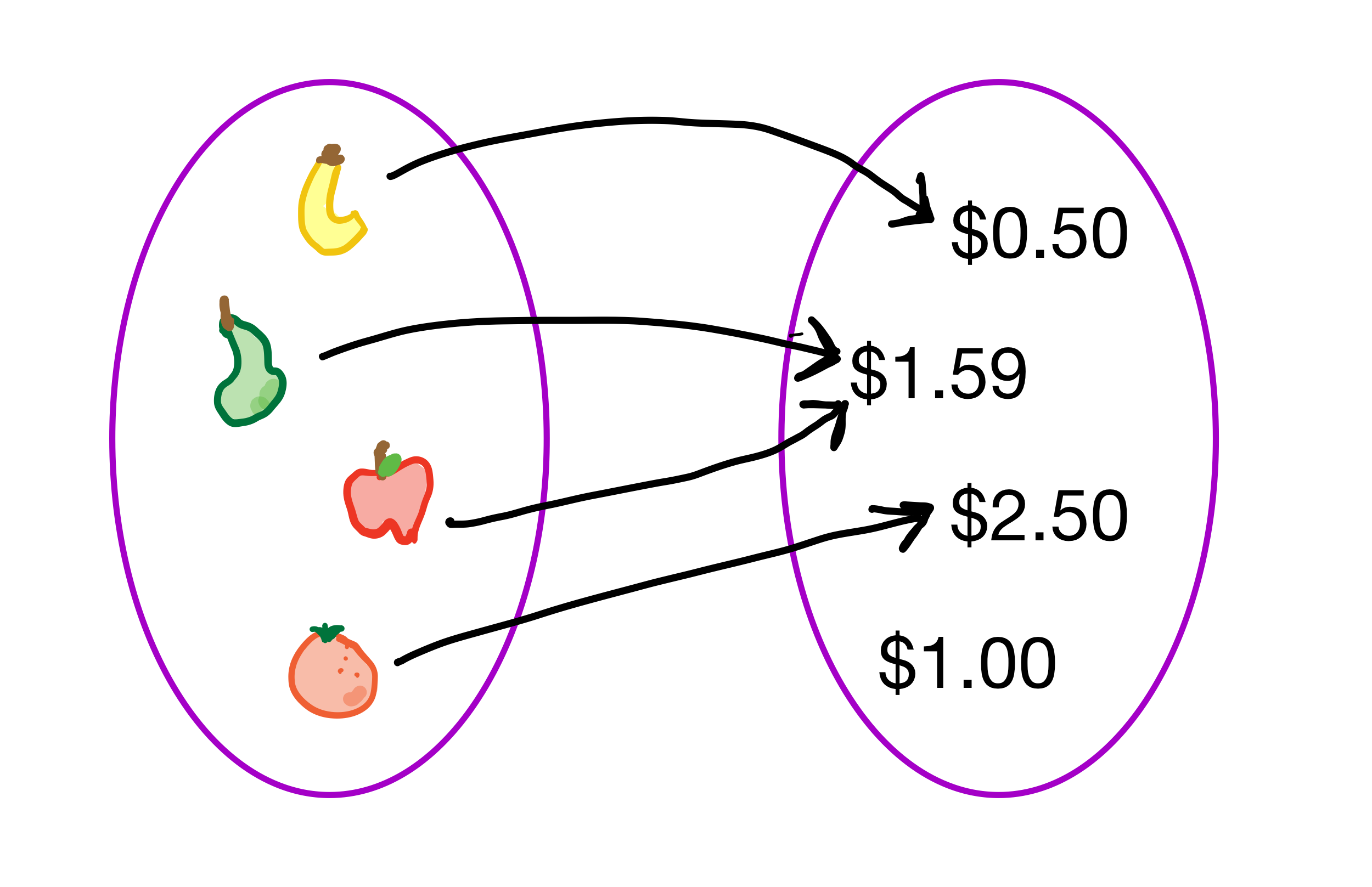
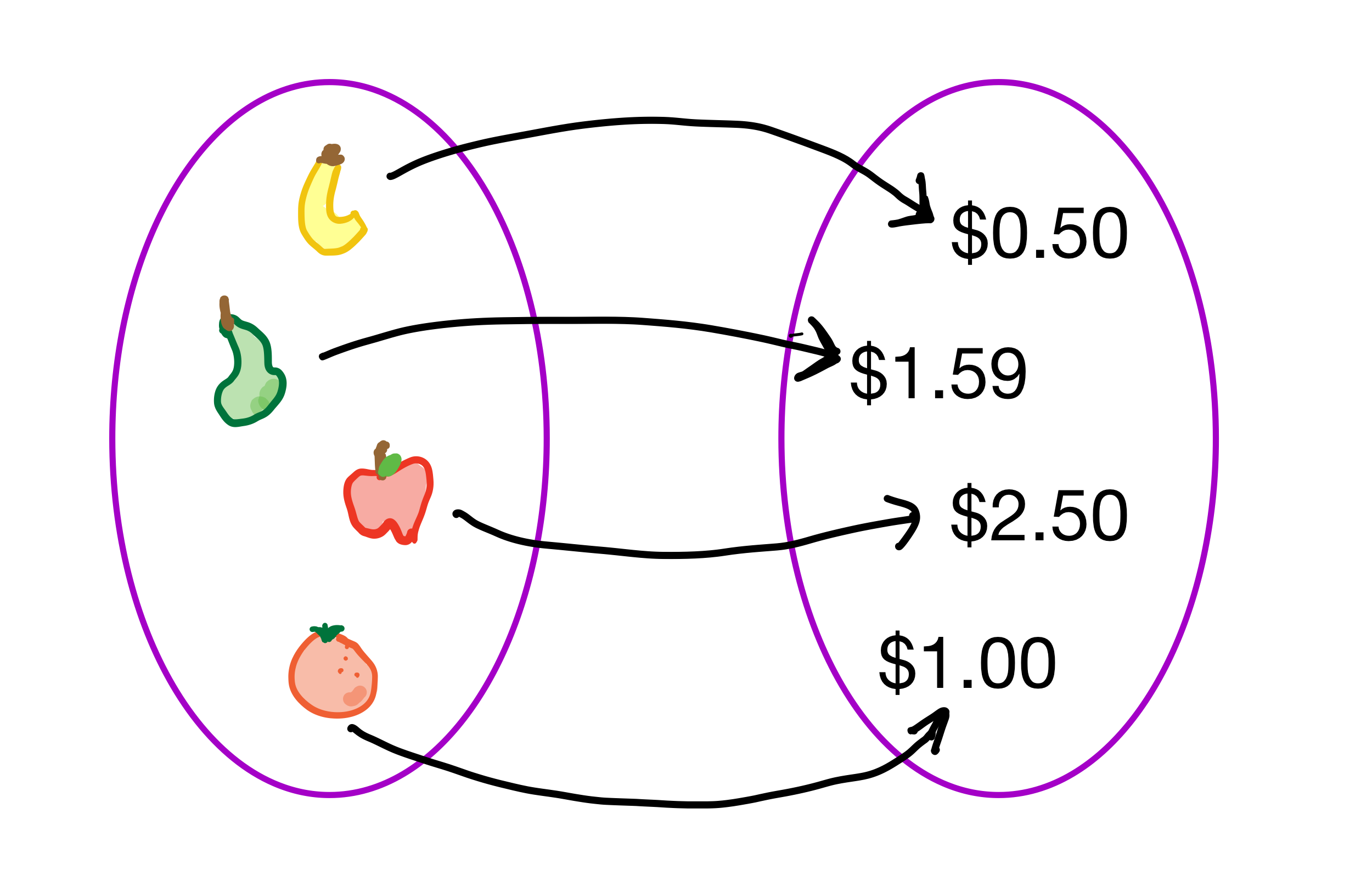
The first diagram does not have an inverse because there are two objects on the left pointing to the same object on the right. But the second diagram does have an inverse. We can find this inverse by simply reversing the direction of each arrow as follows

Next, consider the functions and given in the following tables.

     

For any function, the question of whether or not it has an inverse comes down to whether or not the process of the function can be reliably reversed. For functions given in table form such as and , we essentially ask if it’s possible to switch the input and output columns and have the new resulting table also represent a function.

The function does not have an inverse function because there are two different inputs that lead to the same output: and . If we attempt to reverse this process, we have a situation where the input would correspond to two potential outputs, and , which is not allowed for a function.

However, the function does have an inverse function because when we reverse the columns in the table each input (in order, , , , , ) indeed corresponds to one and only one output (in order, , , , , ). We can thus make observations such as , which is the same as saying that , just from a different perspective.

Now, consider the functions and represented by the following graphs.

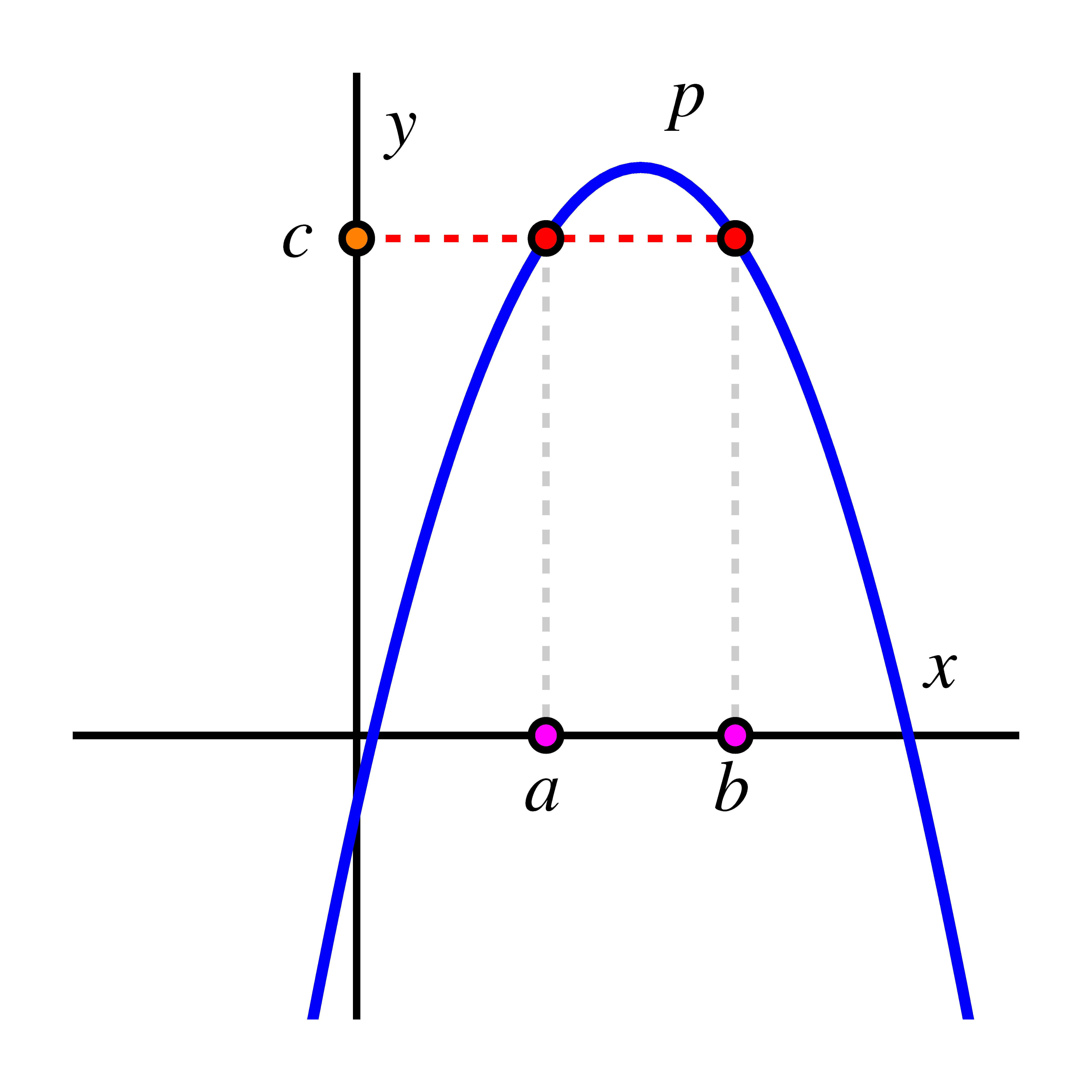
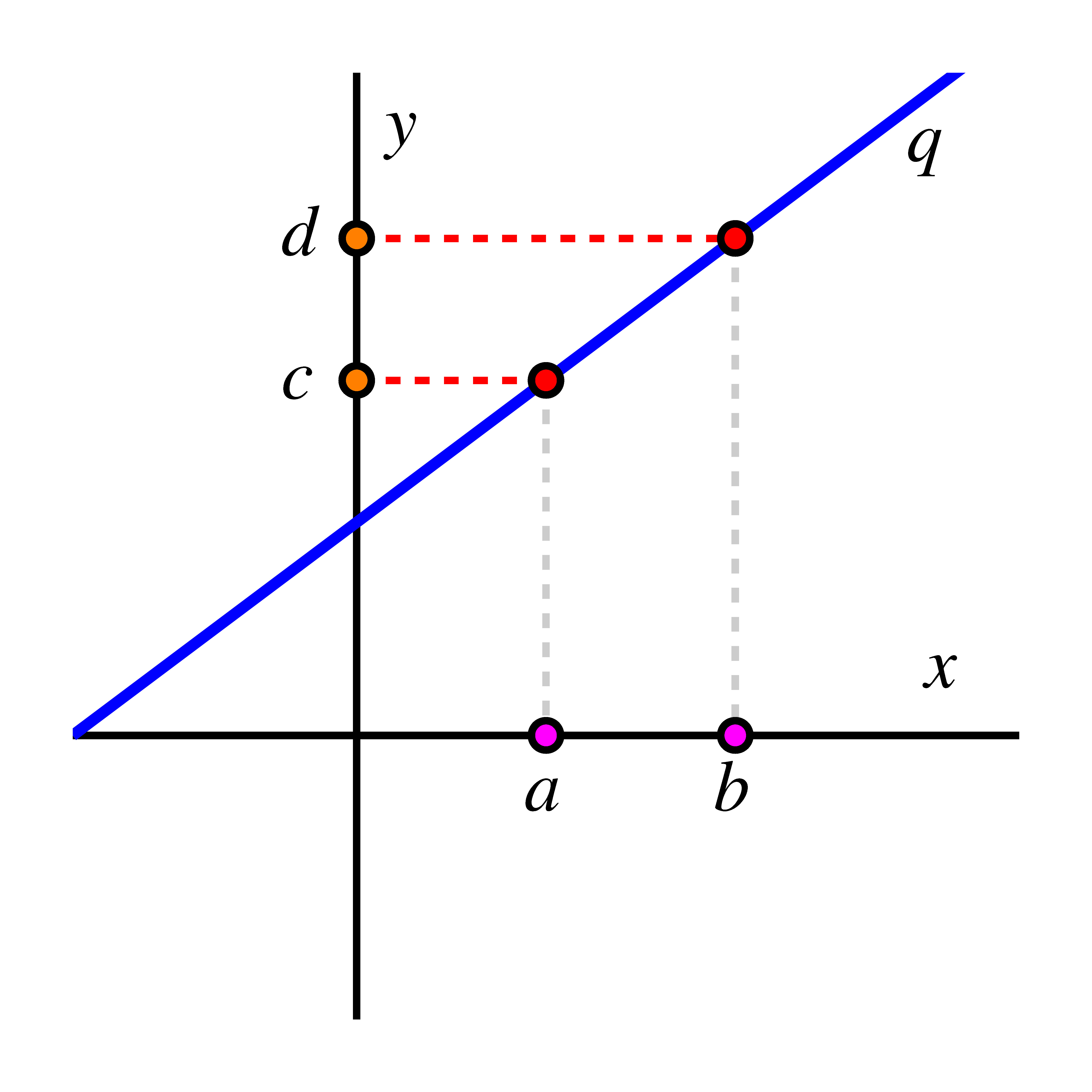
Recall that when a point such as lies on the graph of a function , this means that the input , which represents a value on the horizontal axis, corresponds with the output that is represented by a value on the vertical axis. In this situation, we write . We note explicitly that is a function because its graph passes the vertical line test: any vertical line intersects the graph of once, and thus each input corresponds to one output.

If we attempt to change perspective and use the graph of to view as a function of , we see that this fails because the output value is associated with two different inputs, and . Said differently, because the horizontal line intersects the graph of at both and (as shown in the figure), we cannot view as the input to a function process that produces the corresponding -value. Therefore, does not have an inverse function. Note: We can have a relation that switches the - and -values of , but it won’t be a function!

On the other hand, provided that the behavior seen in the figure continues, the function does have an inverse because we can view as a function of via the graph. This is because for any choice of , there corresponds one that results from . We can think of this visually by starting at a value such as on the -axis, moving horizontally to where the line intersects the graph of , and then moving down to the corresponding location (here ) on the horizontal axis. From the behavior of the graph of (a straight line that is always increasing), we see that this correspondence will hold for any choice of , and thus indeed is a function of . From this, we can say that indeed has an inverse function. We thus can write that , which is a different way to express the equivalent fact that .

The two examples above illustrate an important requirement for a function to have an inverse function. For a function to have an inverse, different inputs must go to different outputs, or else we will run into the same problems as we did in the examples of and above.

In particular, the graphical observations that we made for the function in the last example provide a general test for whether or not a function given by a graph has a corresponding inverse function.

Consider the functions and defined by
a.
Solve the equation for . Can be expressed as a single function of ? What could go wrong?
b.
Is one-to-one?
c.
Find and . Compare them; is is one-to-one?
d.
Solve the equation for . Can be expressed as a single function of ? What could go wrong?

To check your answers for (b) and (b) above, you could try graphing and on Desmos and applying the horizontal line test.

Graphical properties of inverse functions

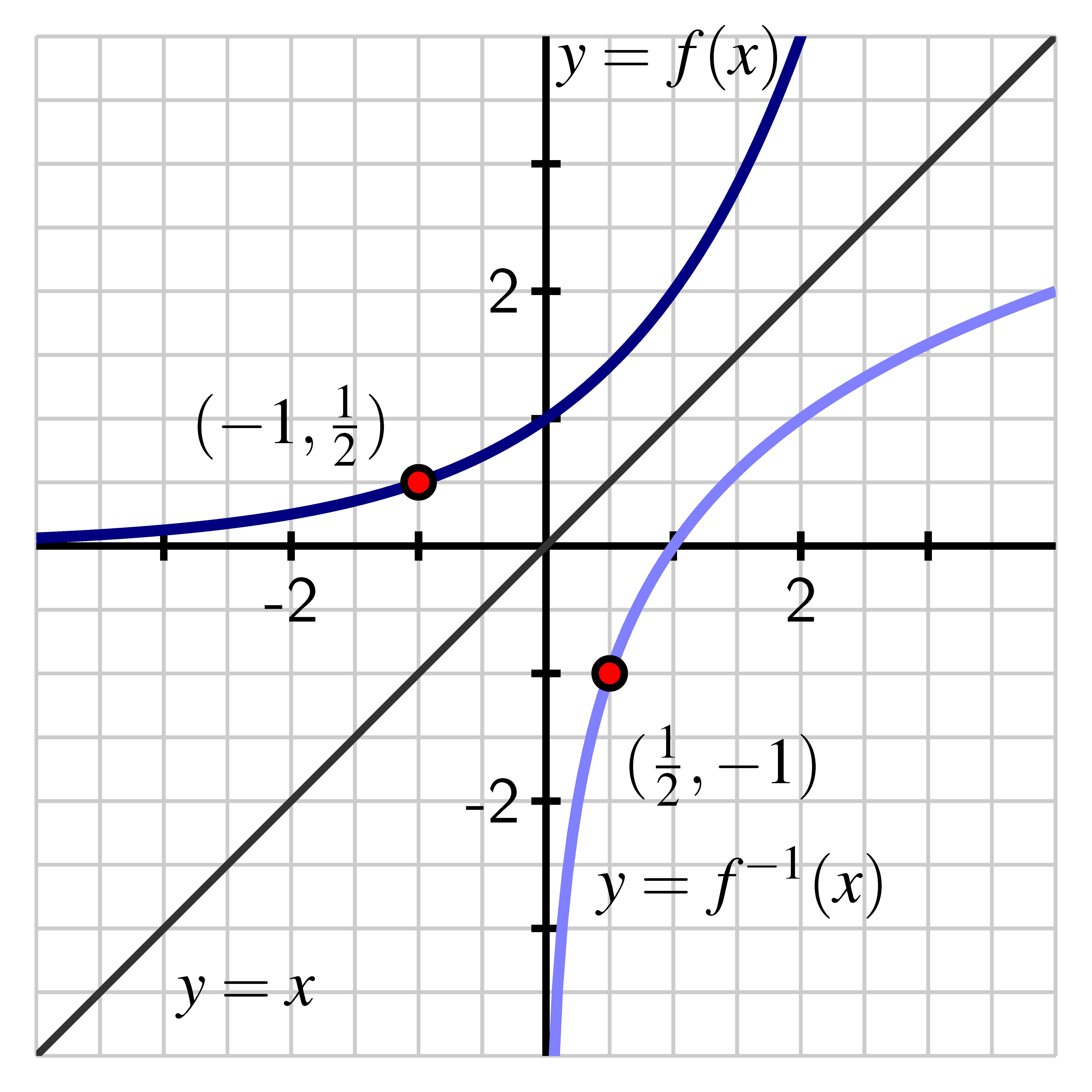
Finally, we mention an important relationship between the graph of a function and the graph of its inverse function. If is one-to-one, then recall that a point lies on the graph of if and only if . From this, since is one-to-one, we can equivalently say that . Hence, the point lies on the graph of .

The last item above leads to a special relationship between the graphs of and when viewed on the same coordinate axes. In that setting, we need to view as the input of each function (since it’s the horizontal coordinate) and as the output. If we know a particular input-output relationship for , say , then it follows that . We observe that the points and are reflections of each other across the line . Because such a relationship holds for every point on the graph of , this means that the graphs of and are reflections of one another across the line , as seen in the figure below.