We practice communicating mathematical explanations through fractions and percents.
- (a)
- Using drawing to reason and justify mathematics
- (b)
- Communicating mathematical explanations to others.
Fractions
Fractions are writen in the form where and are numbers. For example, let’s consider and let’s say we know this is a fraction of sweet rolls. To interpret this fraction, we need to know what the ‘whole’ is. Are we talking about a fraction of sweet rolls? sweet roll? Let’s say sweet roll is the whole. Now we’ll divide the sweet roll into equal size pieces because the denominator is . Each of those pieces is of the sweet roll. So shading pieces of size gives us of sweet roll.
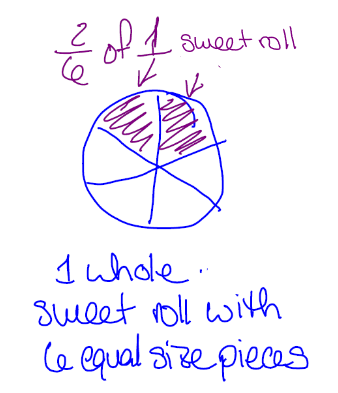
- Camila has invited 9 guests over for breakfast. However, she only made 8 churros. On top of that, only 7 guests like cinnamon sugar on their churro. Draw a picture to illustrate how Camila can ensure each guest gets the same amount of churro and gets their desired cinnamon sugar/none on their churro. Then use the picture to determine what fraction of the churros should be coated with with cinnamon sugar.
- Chris made sweet potato pies to split between him and friends. But he accidentally used to different sized pie dishes so they’re different sizes! How can Chris split up the pies so each person gets the same amount of pie?
Percentages
Percentages are a special type of ratio that can be expressed as a fraction in the form . For example,
The word ‘percent’ comes from the Latin ‘per centum’ which mean ‘by the
one-hundred’. The prefix ‘cent’ is all around us. For example, a ‘century’ is years,
‘centimeter’ is of a meter, a ‘cent’ is of a dollar. In spanish, ‘cien’ is . You can also
think of percent as a unit. per or out of every .
- Chandice has started collecting small toy vehicles and has toy vehicles. Of the vehicles, are race cars, are pick-up trucks, are semi-trucks, and are fire trucks. Without using a calculator, what percent of Chandice’s toy vehicles are race cars? Draw a picture that supports your computations.
- Kajal wants to give a tip for food delivery but needs to enter the tip amount as a dollar amount. She purchased worth of food. Without using a calculator, what is the amount Kajal should give as tip?
Percent Increase and Decrease
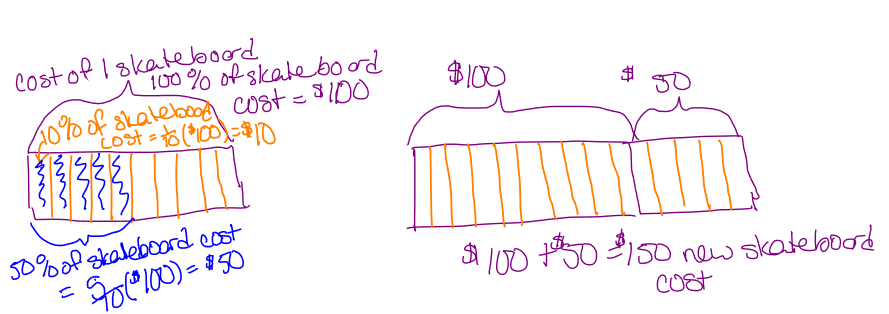
In the problems where percent increases or decreases are calculated, we calculate not only the percent change, but also the “actual value” change as well.
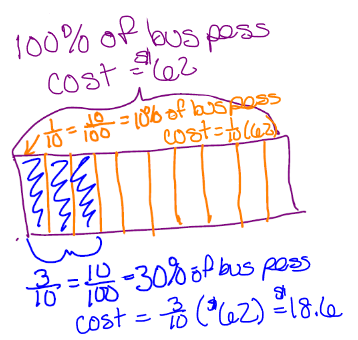
Therefore, to find the value we need, we calculate of by
is the discount. Seniors pay: for a -day bus pass.
It can be helpful to have terminology to describe the answers to these type of problems.
Absolute change is the “actual value” change that occurred.
Relative change is the percent change that occurred.
The absolute change for the bus pass was – the actual dollar amount that the price changed. The relative change for the bus pass was 30% decrease – the percent or proportion that the dollar amount was changed.
Now we can deal with the percent decrease. Remember to decrease from the new amount ($150) and not the original ($100). After subtracting this amount from $150 we will have the final amount.
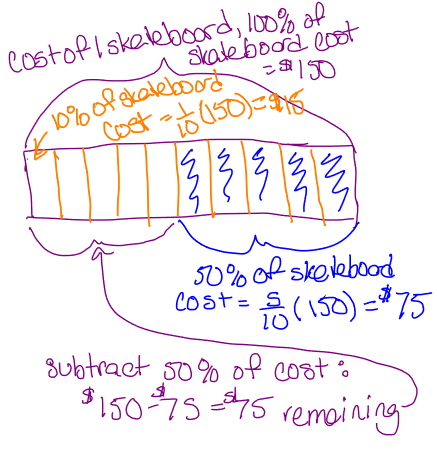
After raising the $100 price by 50% and lowering it be 50% the final price became $75 an overall decrease of 25%!
- What was the total percent change in attendees over the two years? Let’s first try this problem with a specific number of attendees to start with. In your group, find the change if there were certain number of attendees in 2011 (choose a 3 digit number that does NOT end with a 0). Then try to think about how to do this problem without knowing a specific number of attendees.
- It might be tempting to say that the change over the two years was a increase. Why might someone think it is a increase (i.e., how do you come up with from the numbers in the problem?)
- Why is incorrect?
- Understand the problem
- Restate the problem in your own words
- Use drawings to understand the problem
- Consider the definitions of mathematical terms and knowledge related to those terms, such as theorems. Ask, what do I know about this topic that might help me solve this problem?
- Create a plan
- Break the problem down into smaller pieces
- Test numbers
- Look for patterns
- Check your assumptions
- Carry out the plan while monitoring your progress
- Throughout the process, check that your steps make sense
- Check for arithmetic or algebra mistakes
- If your plan doesn’t work, that’s okay! Create another plan.
- Evaluate your process and solution
- Attend to units to check if your answer makes sense
- Use an estimate to check if your answer makes sense
- What did or didn’t go well with your plan? How can that inform your future work on problems?
- What mistakes did you make along the way? How can you catch those mistakes in the future?