Triple Integrals in Cartesian Coordinates

$\newenvironment {prompt}{}{} \newcommand {\DeclareMathOperator }[2]{\@OldDeclareMathOperator {##1}{##2}\immediate \write \myfile {\unexpanded {\DeclareMathOperator }{\unexpanded {##1}}{\unexpanded {##2}}}} \newcommand {\reserved@a }[2]{} \newcommand {\HyperFirstAtBeginDocument }[0]{\AtBeginDocument } \newcommand {\reserved@a }[1]{} \newcommand {\reserved@a }[2]{} \newcommand {\AppendGraphicsExtensions }[0]{\@ifundefined {Gin@extensions}{\let \Gin@extensions \@empty }{}\@ifstar {\grfext@Append \grfext@Check }{\grfext@Append \grfext@@Add }} \newcommand {\PrependGraphicsExtensions }[0]{\@ifundefined {Gin@extensions}{\let \Gin@extensions \@empty }{}\@ifstar {\grfext@Prepend \grfext@Check }{\grfext@Prepend \grfext@@Add }} \newcommand {\RemoveGraphicsExtensions }[1]{\@ifundefined {Gin@extensions}{\def \Gin@extensions {}}{\edef \grfext@tmp {\zap@space ##1 \@empty }\@for \grfext@ext :=\grfext@tmp \do {\def \grfext@next {\let \grfext@tmp \Gin@extensions \@expandtwoargs \@removeelement \grfext@ext \Gin@extensions \Gin@extensions \ifx \grfext@tmp \Gin@extensions \let \grfext@next \relax \fi \grfext@next }\grfext@next }}\grfext@Print \RemoveGraphicsExtensions } \newcommand {\epstopdfsetup }[0]{\setkeys {ETE}} \newcommand {\epstopdfcall }[1]{\ifETE@InsideSetfile \expandafter \@firstoftwo \else \expandafter \@secondoftwo \fi {‘##1}{\Gin@base \Gin@ext }} \newcommand {\epstopdfDeclareGraphicsRule }[4]{\ifx \\##4\\\@PackageError {epstopdf-base}{Conversion command is missing}\@ehc \else \begingroup \@ifundefined {Gin@rule@##1}{}{\@PackageInfo {epstopdf-base}{Redefining graphics rule for ‘##1’}}\endgroup \@namedef {Gin@rule@##1}####1{{##2}{##3}{\epstopdfcall {##4}}}\fi } \newcommand {\GetTitleStringSetup }[0]{\setkeys {gettitlestring}} \newcommand {\GetTitleString }[0]{\ifGTS@expand \expandafter \GetTitleStringExpand \else \expandafter \GetTitleStringNonExpand \fi } \newcommand {\GetTitleStringExpand }[1]{\def \GetTitleStringResult {##1}\begingroup \GTS@DisablePredefinedCmds \GTS@DisableHook \edef \x {\endgroup \noexpand \def \noexpand \GetTitleStringResult {\GetTitleStringResult }}\x } \newcommand {\GetTitleStringNonExpand }[1]{\def \GetTitleStringResult {##1}\global \let \GTS@GlobalString \GetTitleStringResult \begingroup \GTS@RemoveLeft \GTS@RemoveRight \endgroup \let \GetTitleStringResult \GTS@GlobalString } \newcommand {\GTS@DisableHook }[0]{} \newcommand {\label@hook }[0]{} \newcommand {\@currentlabelname }[0]{} \newcommand {\reserved@a }[0]{} \newcommand {\@safe@activestrue }[0]{} \newcommand {\@safe@activesfalse }[0]{} \newcommand {\nameref }[0]{\@ifstar \T@nameref \T@nameref } \newcommand {\Sectionformat }[2]{##1} \newcommand {\vnameref }[1]{\unskip ~\nameref {##1}\@vpageref [\unskip ]{##1}} \newcommand {\ref }[0]{\@ifstar \@refstar \T@ref } \newcommand {\pageref }[0]{\@ifstar \@pagerefstar \T@pageref } \newcommand {\nameref }[0]{\@ifstar \@namerefstar \T@nameref } \newcommand {\reserved@a }[2]{} \newcommand {\reserved@a }[0]{\AtBeginDocument } \newcommand {\reserved@a }[1]{} \newcommand {\reserved@a }[2]{}$

Objectives:

1.: Be comfortable setting up and computing triple integrals in Cartesian coordinates.
2.: Understand what a triple integral represents geometrically.
3.: Know what the triple integral of $f(x,y,z) = 1$ represents.

Recap Video

Here is a video highlights the main points of the section.

Example Video

Here is an example of setting up bounds for a triple integral in Cartesian coordinates.

If $R$ is the region bounded by $x=3z^2$ , $y=x$ , $y = 0$ , and $x=12$ . If $f(x,y,z)$ is any continuous function, set up $\displaystyle \iiint _R f(x,y,z)dV$ .

Problems

Let $B$ be the box $[0,5] \times [2,8] \times [0,1]$ . Evaluate $\displaystyle \iiint _B z^4dV$ .

Remember the first interval is the interval for $x$ , the second for $y$ , and the third for $z$ . We can therefore set this integral up as, for example, $\int _{x=\answer {0}}^{x=\answer {5}} \int _{y=\answer {2}}^{y=\answer {8}} \int _{z=\answer {0}}^{z=\answer {1}} \answer {z^4}dz\,dy\,dx.$ We can evaluate this integral one variable at a time (like we do double integrals), and we get an answer of $\answer {6}$ .

Let $R$ be the filled in tetrahedron with vertices $(0,0,0)$ , $(4,0,0)$ , $(0,4,0)$ , and $(0,0,6)$ . Find the volume of $R$ .

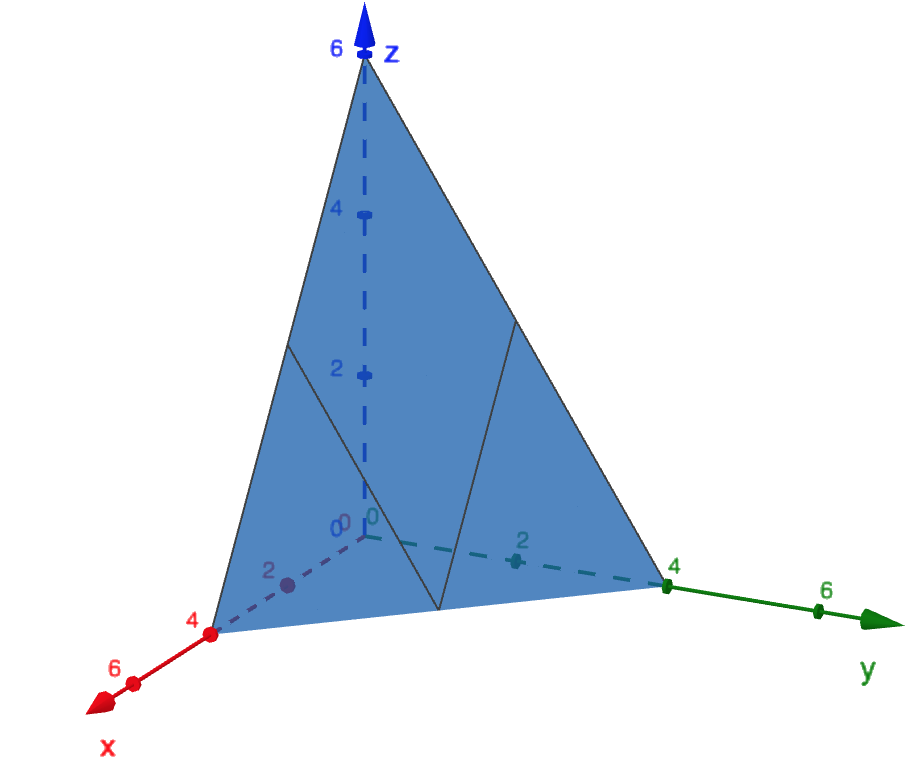
To find the volume, our integrand will be $f(x,y,z) = \answer {1}$ . For the region: three of the faces of the tetrahedron are the planes $x = 0$ , $y = 0$ , $z=0$ . The last one is the plane $\answer {3}x+\answer {3}y+\answer {2}z = 12.$ If we want to set this integral up in $z$ first, we must fix $x$ and $y$ and see what $z$ is doing. For this region, we see that $z$ moves from $0$ to the tilted plane. The “ $z$ ” integral will therefore have bounds: $\answer {0} \leq z \leq \answer {\frac {12-3x-3y}{2}}.$ To get the $x$ and $y$ bounds, we now project this region $R$ into the $xy$ -plane. This will be a triangle with vertices $(0,0),(\answer {4},0),(0,\answer {4}).$ We now set this integral up in $x$ and $y$ . For example, we want to integrate with respect to $y$ next, the bounds for $y$ will be $\answer {0} \leq y \leq \answer {4-x},$ and finally the bounds for $x$ will be $\answer {0} \leq x\leq \answer {4}.$ Thus, the integral will become $\int _0^4\int _0^{4-x} \int _0^{\frac {12-3x-3y}{2}} 1 dz\,dy\,dx.$ It evaluates to $\answer {16}$ .

If $f(x,y,z) = z$ and $R$ is the region given by $x \geq 0$ , $z \geq 0$ , $y 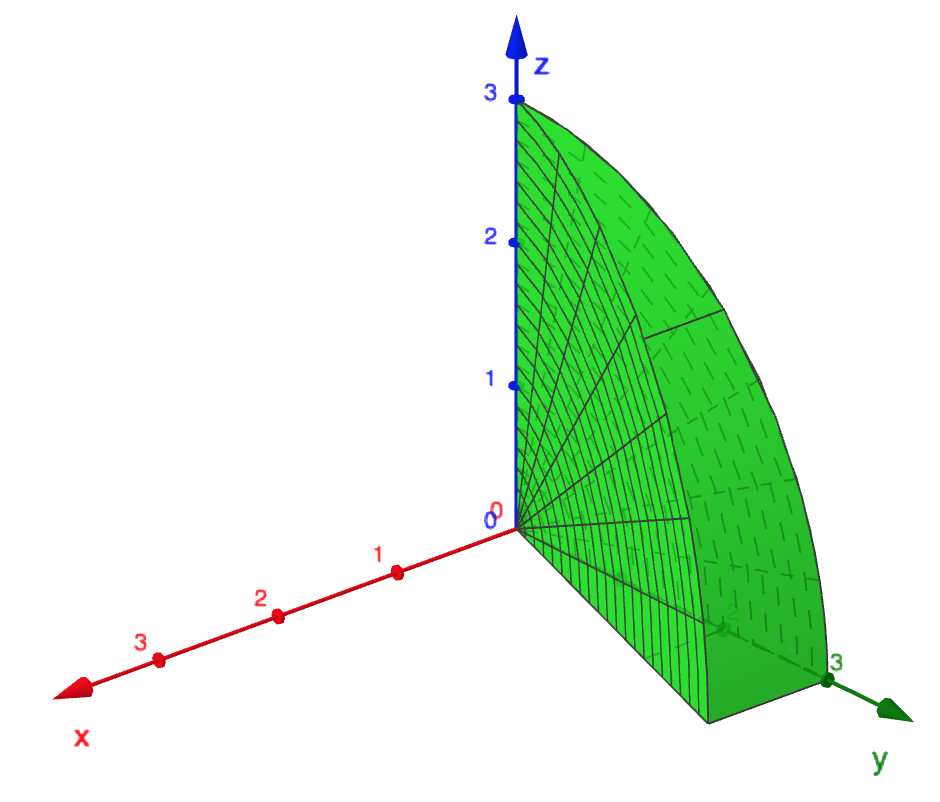\geq 3x$ and $y^2+z^2 \leq 9$ , evaluate $\displaystyle \iiint _R f(x,y,z)dV$ .

The region is shown above. We can try setting this up with $dz$ first. If we do that, then we see that $\answer {0} \leq z \leq \answer {\sqrt {9-y^2}}.$ Projecting into the $xy$ -plane gives us a triangle bounded by $y = 3x$ , $y=3$ , and $x=0$ . Setting up a double integral over this triangle in the order $dy\,dx$ would give the bounds $\answer {3x} \leq y \leq \answer {3},$ $\answer {0} \leq x \leq \answer {1}.$ Thus, we get a triple integral which looks like $\int _0^1 \int _{3x}^3 \int _0^{\sqrt {9-y^2}} z \,dz\,dy\,dx.$ Evaluating this gives an answer of $\answer {27/8}$ .

Set up the triple integral from the previous problem with $dx$ first and then separately with $dy$ first.

If we do $dx$ first, then we would have $\int _{\answer {0}}^{\answer {3}} \int _{\answer {0}}^{\answer {\sqrt {9-y^2}}} \int _{\answer {0}}^{\answer {y/3}} z \,dx\,dz\,dy.$
If we were to do $dy$ first, we would get $\int _{\answer {0}}^{\answer {1}} \int _{\answer {0}}^{\answer {\sqrt {9-9x^2}}} \int _{\answer {3x}}^{\answer {\sqrt {9-z^2}}} z\,dy\,dz\,dx.$

If $f(x,y,z)=z$ and $R$ is the region in the first quadrant bounded by $2x-y = 0$ , $y+z=2$ , $x=0$ , and $z=0$ , then $\displaystyle \iiint _R f(x,y,z)dV = \answer {\frac {1}{3}}$ .

If we do $z$ first, then $z$ goes from $z=0$ to $z=\answer {2-y}$ . In the $xy$ -plane, the region is bounded by $y=2x$ , $x=0$ , and $y=2$ . So the triple integral should be $\int _0^1 \int _{2x}^2 \int _0^{2-y} zdz\,dy\,dx.$

The integral $\displaystyle \int _0^1 \int _x^1 \int _y^1 f(x,y,z)dz\,dy\,dx$ in the order $dx \, dy\, dz$ is $\int _{\answer {0}}^{\answer {1}} \int _{\answer {0}}^{\answer {z}} \int _{\answer {0}}^{\answer {y}} f(x,y,z)dx\,dy\,dz.$

This region is bounded by the planes $z = y$ , $z= 1$ , $y = x$ , $x=0$ , and $y=0$ . It becomes $\int _0^1 \int _0^z \int _0^y f(x,y,z)dx\,dy\,dz.$

The integral of a function $f(x,y,z)$ over the region bounded by $z = \sqrt {x^2+y^2}$ and $z=4$ in the order $dx\,dy\,dz$ has setup $\int _{\answer {0}}^{\answer {4}}\int _{\answer {-z}}^{\answer {z}} \int _{\answer {-\sqrt {z^2-y^2}}}^{\answer {\sqrt {z^2-y^2}}} f(x,y,z)dx\,dy\,dz.$

To get the $x$ bounds, solve for $x$ in the cones equation to get $x = \pm \sqrt {z^2-y^2}$ , so $x$ will go from $-\sqrt {z^2-y^2}$ to $\sqrt {z^2-y^2}$ . We now have to project onto the $yz$ -plane. We know $z=4$ is one of the bounds of our projected region. To get the others, we find the intersection of the two $x$ bounds, i.e. $-\sqrt {z^2-y^2} = \sqrt {z^2-y^2}$ . This gives $z = \pm y$ . So we have the region in the $yz$ -plane bounded by $z = -y$ , $z=y$ , and $z=4$ . This is easiest in the order $dy\,dz$ , and we get $\answer {-z} \leq y \leq \answer {z}$ and $0 \leq z \leq \answer {4}$ .