Review of Polar Coordinates

$\newenvironment {prompt}{}{} \newcommand {\DeclareMathOperator }[2]{\@OldDeclareMathOperator {##1}{##2}\immediate \write \myfile {\unexpanded {\DeclareMathOperator }{\unexpanded {##1}}{\unexpanded {##2}}}} \newcommand {\reserved@a }[2]{} \newcommand {\HyperFirstAtBeginDocument }[0]{\AtBeginDocument } \newcommand {\reserved@a }[1]{} \newcommand {\reserved@a }[2]{} \newcommand {\AppendGraphicsExtensions }[0]{\@ifundefined {Gin@extensions}{\let \Gin@extensions \@empty }{}\@ifstar {\grfext@Append \grfext@Check }{\grfext@Append \grfext@@Add }} \newcommand {\PrependGraphicsExtensions }[0]{\@ifundefined {Gin@extensions}{\let \Gin@extensions \@empty }{}\@ifstar {\grfext@Prepend \grfext@Check }{\grfext@Prepend \grfext@@Add }} \newcommand {\RemoveGraphicsExtensions }[1]{\@ifundefined {Gin@extensions}{\def \Gin@extensions {}}{\edef \grfext@tmp {\zap@space ##1 \@empty }\@for \grfext@ext :=\grfext@tmp \do {\def \grfext@next {\let \grfext@tmp \Gin@extensions \@expandtwoargs \@removeelement \grfext@ext \Gin@extensions \Gin@extensions \ifx \grfext@tmp \Gin@extensions \let \grfext@next \relax \fi \grfext@next }\grfext@next }}\grfext@Print \RemoveGraphicsExtensions } \newcommand {\epstopdfsetup }[0]{\setkeys {ETE}} \newcommand {\epstopdfcall }[1]{\ifETE@InsideSetfile \expandafter \@firstoftwo \else \expandafter \@secondoftwo \fi {‘##1}{\Gin@base \Gin@ext }} \newcommand {\epstopdfDeclareGraphicsRule }[4]{\ifx \\##4\\\@PackageError {epstopdf-base}{Conversion command is missing}\@ehc \else \begingroup \@ifundefined {Gin@rule@##1}{}{\@PackageInfo {epstopdf-base}{Redefining graphics rule for ‘##1’}}\endgroup \@namedef {Gin@rule@##1}####1{{##2}{##3}{\epstopdfcall {##4}}}\fi } \newcommand {\GetTitleStringSetup }[0]{\setkeys {gettitlestring}} \newcommand {\GetTitleString }[0]{\ifGTS@expand \expandafter \GetTitleStringExpand \else \expandafter \GetTitleStringNonExpand \fi } \newcommand {\GetTitleStringExpand }[1]{\def \GetTitleStringResult {##1}\begingroup \GTS@DisablePredefinedCmds \GTS@DisableHook \edef \x {\endgroup \noexpand \def \noexpand \GetTitleStringResult {\GetTitleStringResult }}\x } \newcommand {\GetTitleStringNonExpand }[1]{\def \GetTitleStringResult {##1}\global \let \GTS@GlobalString \GetTitleStringResult \begingroup \GTS@RemoveLeft \GTS@RemoveRight \endgroup \let \GetTitleStringResult \GTS@GlobalString } \newcommand {\GTS@DisableHook }[0]{} \newcommand {\label@hook }[0]{} \newcommand {\@currentlabelname }[0]{} \newcommand {\reserved@a }[0]{} \newcommand {\@safe@activestrue }[0]{} \newcommand {\@safe@activesfalse }[0]{} \newcommand {\nameref }[0]{\@ifstar \T@nameref \T@nameref } \newcommand {\Sectionformat }[2]{##1} \newcommand {\vnameref }[1]{\unskip ~\nameref {##1}\@vpageref [\unskip ]{##1}} \newcommand {\ref }[0]{\@ifstar \@refstar \T@ref } \newcommand {\pageref }[0]{\@ifstar \@pagerefstar \T@pageref } \newcommand {\nameref }[0]{\@ifstar \@namerefstar \T@nameref } \newcommand {\reserved@a }[2]{} \newcommand {\reserved@a }[0]{\AtBeginDocument } \newcommand {\reserved@a }[1]{} \newcommand {\reserved@a }[2]{}$

Objectives:

1.: Review polar coordinates.

Recall that the transformation to get from polar $(r,\theta )$ coordinates to Cartesian $(x,y)$ coordinates is $x =r\cos (\theta ),\quad y = r\sin (\theta ).$ The picture relating $(r,\theta )$ to $(x,y)$ is shown below:

It is useful to note that $r^2 = x^2+y^2$ .

The point $(r,\theta ) = (6,\pi /3)$ corresponds to the Cartesian point $(x,y) = (\answer {3},\answer {3\sqrt {3}}).$

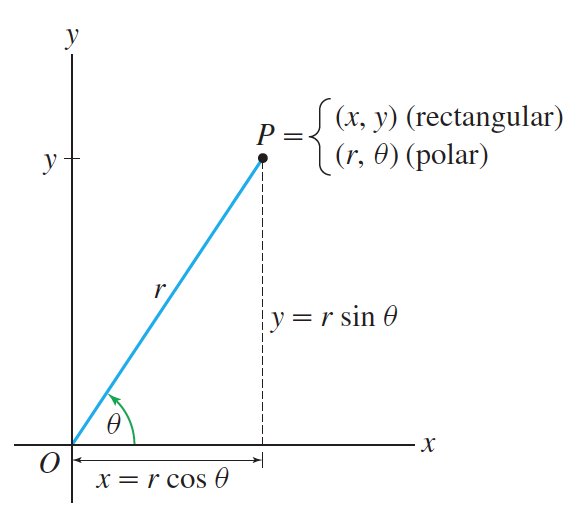
Remember that polar coordinates was great for describing certain objects, such as circles.

Transform the equation $x^2+y^2 = 1$ into polar coordinates.

To transform the equation into polar, we plug in $x = r\cos (\theta )$ , $y = r\sin (\theta )$ into the equation to get $\answer {r^2} = 1,$ which means the equation is $r = \answer {1}$ .

One issue we will encounter with polar is the non-uniqueness of points. From now on, we will restrict ourselves to the situation where $r \geq 0$ (i.e. we will not look at negative $r$ -values). This will help us a little bit later.

What does $r=0$ look like in Cartesian coordinates?

The point $(x,y) = (0,0)$ The $x$ -axis The $y$ -axis The line $y=x$

Transform the line $y =x$ into polar coordinates.

To transform the equation, we plug in $x = r\cos (\theta )$ , $y = r\sin (\theta )$ to get $r\sin (\theta ) = r\cos (\theta ).$ Since $r=0$ is just a point (and will not describe the whole line), we can divide by $r$ to get $\sin (\theta ) = \cos (\theta ).$ On the interval $[0,2\pi ]$ , this happens when $\theta = \answer {\frac {\pi }{4}}, \frac {5\pi }{4}.$ Therefore, the line can be described as $\theta = \answer {\frac {\pi }{4}}$ and $\theta = \frac {5\pi }{4}$ . Note that the former gives the portion of the line with $x \geq 0$ and the latter gives the portion of the line with $x \leq 0$ .

The line $x=1$ in polar coordinates becomes $r = \answer {\frac {1}{\cos (\theta )}}.$

The circle $(x-1)^2+y^2 = 1$ in polar coordinates becomes $r = \answer {2\cos (\theta )}.$

Expand the circle to get $x^2-2x+1+y^2=1$ , or $x^2+y^2-2x=0$ . In polar, this is $r^2-2r\cos (\theta ) = 0$ . Now solve for $r$ .