Global Extrema

$\newenvironment {prompt}{}{} \newcommand {\DeclareMathOperator }[2]{\@OldDeclareMathOperator {##1}{##2}\immediate \write \myfile {\unexpanded {\DeclareMathOperator }{\unexpanded {##1}}{\unexpanded {##2}}}} \newcommand {\reserved@a }[2]{} \newcommand {\HyperFirstAtBeginDocument }[0]{\AtBeginDocument } \newcommand {\reserved@a }[1]{} \newcommand {\reserved@a }[2]{} \newcommand {\AppendGraphicsExtensions }[0]{\@ifundefined {Gin@extensions}{\let \Gin@extensions \@empty }{}\@ifstar {\grfext@Append \grfext@Check }{\grfext@Append \grfext@@Add }} \newcommand {\PrependGraphicsExtensions }[0]{\@ifundefined {Gin@extensions}{\let \Gin@extensions \@empty }{}\@ifstar {\grfext@Prepend \grfext@Check }{\grfext@Prepend \grfext@@Add }} \newcommand {\RemoveGraphicsExtensions }[1]{\@ifundefined {Gin@extensions}{\def \Gin@extensions {}}{\edef \grfext@tmp {\zap@space ##1 \@empty }\@for \grfext@ext :=\grfext@tmp \do {\def \grfext@next {\let \grfext@tmp \Gin@extensions \@expandtwoargs \@removeelement \grfext@ext \Gin@extensions \Gin@extensions \ifx \grfext@tmp \Gin@extensions \let \grfext@next \relax \fi \grfext@next }\grfext@next }}\grfext@Print \RemoveGraphicsExtensions } \newcommand {\epstopdfsetup }[0]{\setkeys {ETE}} \newcommand {\epstopdfcall }[1]{\ifETE@InsideSetfile \expandafter \@firstoftwo \else \expandafter \@secondoftwo \fi {‘##1}{\Gin@base \Gin@ext }} \newcommand {\epstopdfDeclareGraphicsRule }[4]{\ifx \\##4\\\@PackageError {epstopdf-base}{Conversion command is missing}\@ehc \else \begingroup \@ifundefined {Gin@rule@##1}{}{\@PackageInfo {epstopdf-base}{Redefining graphics rule for ‘##1’}}\endgroup \@namedef {Gin@rule@##1}####1{{##2}{##3}{\epstopdfcall {##4}}}\fi } \newcommand {\GetTitleStringSetup }[0]{\setkeys {gettitlestring}} \newcommand {\GetTitleString }[0]{\ifGTS@expand \expandafter \GetTitleStringExpand \else \expandafter \GetTitleStringNonExpand \fi } \newcommand {\GetTitleStringExpand }[1]{\def \GetTitleStringResult {##1}\begingroup \GTS@DisablePredefinedCmds \GTS@DisableHook \edef \x {\endgroup \noexpand \def \noexpand \GetTitleStringResult {\GetTitleStringResult }}\x } \newcommand {\GetTitleStringNonExpand }[1]{\def \GetTitleStringResult {##1}\global \let \GTS@GlobalString \GetTitleStringResult \begingroup \GTS@RemoveLeft \GTS@RemoveRight \endgroup \let \GetTitleStringResult \GTS@GlobalString } \newcommand {\GTS@DisableHook }[0]{} \newcommand {\label@hook }[0]{} \newcommand {\@currentlabelname }[0]{} \newcommand {\reserved@a }[0]{} \newcommand {\@safe@activestrue }[0]{} \newcommand {\@safe@activesfalse }[0]{} \newcommand {\nameref }[0]{\@ifstar \T@nameref \T@nameref } \newcommand {\Sectionformat }[2]{##1} \newcommand {\vnameref }[1]{\unskip ~\nameref {##1}\@vpageref [\unskip ]{##1}} \newcommand {\ref }[0]{\@ifstar \@refstar \T@ref } \newcommand {\pageref }[0]{\@ifstar \@pagerefstar \T@pageref } \newcommand {\nameref }[0]{\@ifstar \@namerefstar \T@nameref } \newcommand {\reserved@a }[2]{} \newcommand {\reserved@a }[0]{\AtBeginDocument } \newcommand {\reserved@a }[1]{} \newcommand {\reserved@a }[2]{}$

Objectives:

1.: Understand when global maxima of a function $f(x,y)$ on a region $R$ in the $xy$ -plane are guaranteed to exist.
2.: Given a closed and bounded region $R$ in the $xy$ -plane, know how to determine the global maximum and minimum of a continuous function on the region.

Recap Video

The following video recaps the ideas of the section.

To recap:

If $f(x,y)$ is a continuous function on a closed and bounded region $R$ in the $xy$ -plane, then $f(x,y)$ has a global maximum and minimum value.

Let $R$ be a closed and bounded region in the $xy$ -plane, and let $f(x,y)$ be a continuous function. To find the global maximum/minimum value of $f(x,y)$ on $R$ :

First find critical points on the interior of $R$ (assuming this is part of the region) by setting $\nabla f(x,y) = \vec {0}$ or finding points where the gradient is undefined.
On the boundary curves of $R$ , reduce the problem to one variable by finding a relationship among $x$ and $y$ (or parametrizing the curves) and plugging it into $f$ to get a one variable function. Remember to include an interval for your one variable.
For each of the boundary curves of $R$ , find the critical points of your one variable functions on the intervals you found in step 2.
Once you have accumulated all your critical points, plug them into $f(x,y)$ to figure out the biggest/smallest value.

Example Video

The following video works through an example of finding global extrema.

Find the global maximum and global minimum of the function $f(x,y) = xy-x-y+3$ on the filled in triangle with vertices $(0,0)$ , $(2,0)$ , and $(0,4)$ .

Closed and Bounded Regions

Consider the region $x<y<x+1$ shown in the figure.

This region is closednot closed and boundednot bounded .

Consider the region $y \geq |x|$ shown in the figure.

This region is closednot closed and boundednot bounded .

Consider the region $x^2<y<4-x^2$ shown in the figure.

This region is closednot closed and boundednot bounded .

Consider the region $|x|+|y| \leq 1$ shown in the figure.

This region is closednot closed and boundednot bounded .

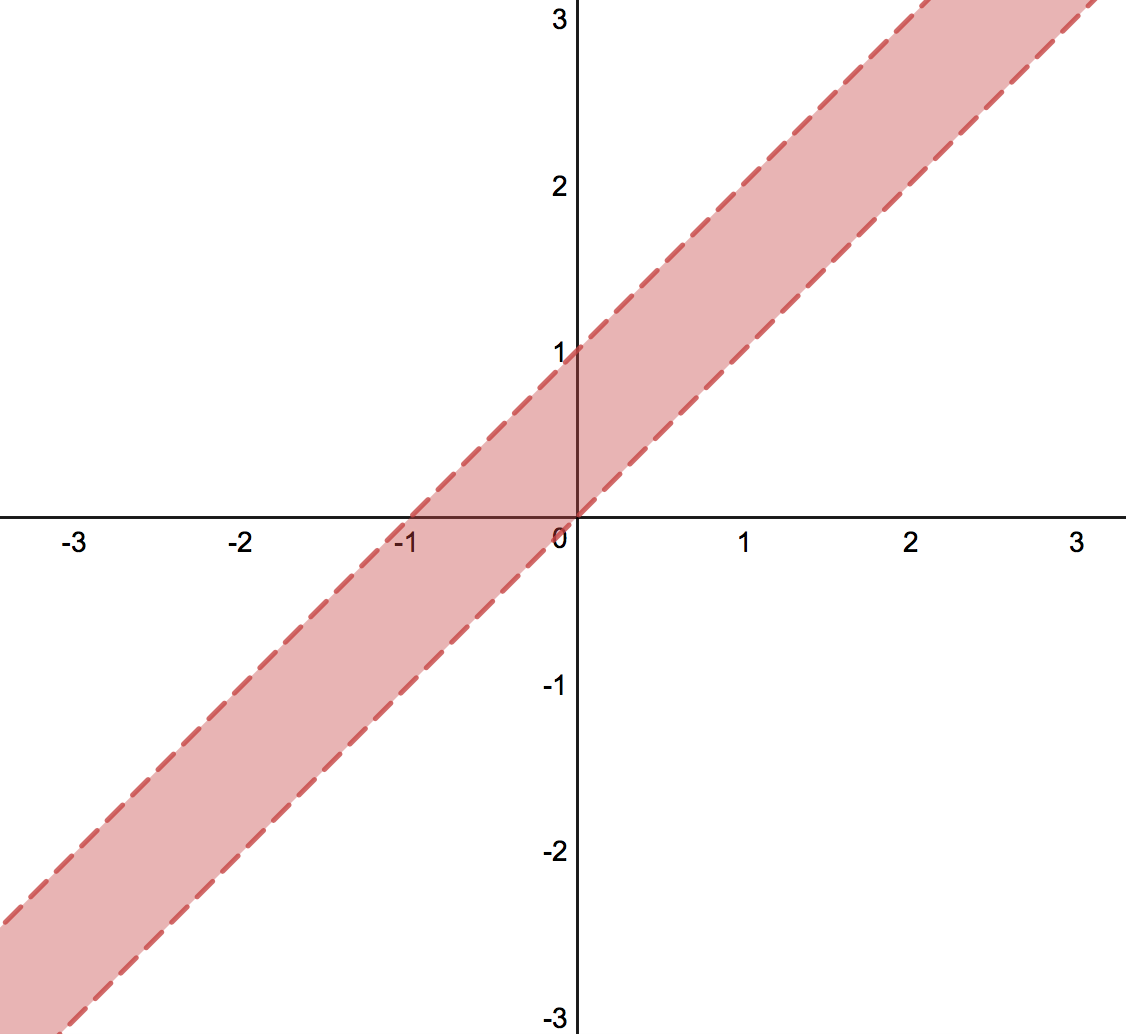
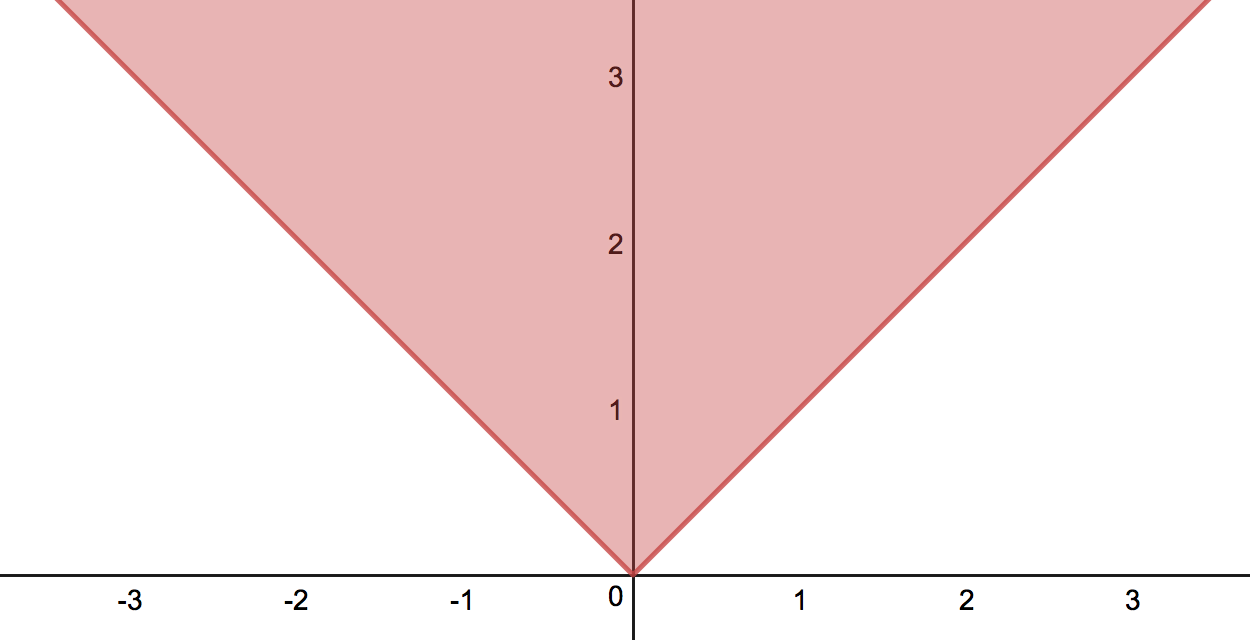
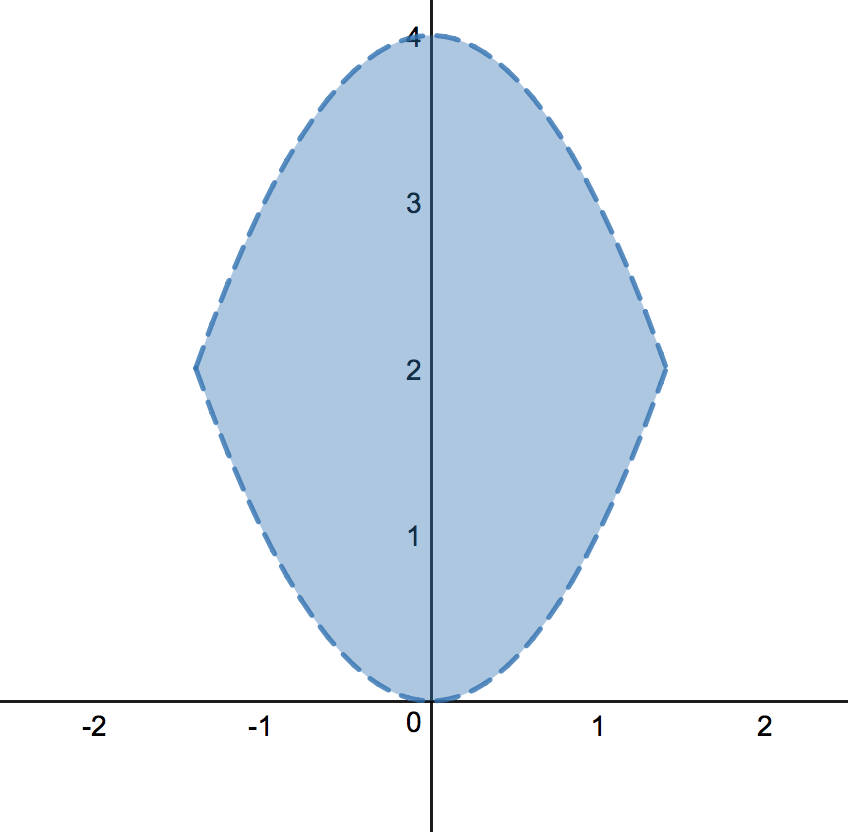
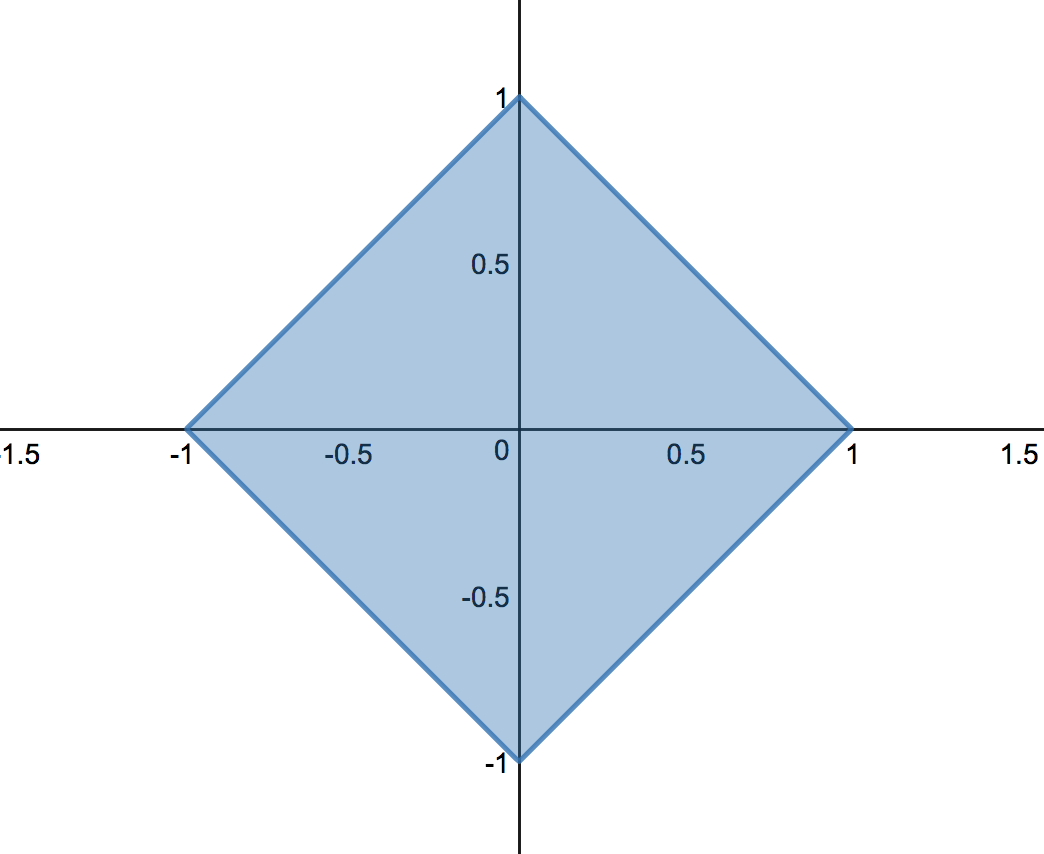
Using your answers from the previous four problems, given a continuous function $f(x,y)$ , on which regions are the global maximum and minimum of $f(x,y)$ guaranteed to exist? Select all that apply.

$R: \,x<y<x+1$ $R: \, y \geq |x|$ $R: \, x^2<y<4-x^2$ $R: \, |x|+|y| \leq 1$

Problems

Find the global maximum value of the function $f(x,y) = x+y-x^2-y^2-xy$ on the square $0 \leq x\leq 2$ , $0 \leq y \leq 2$ .

Steps:

The critical points inside the region are where $\nabla f(x,y) = \vec {0}$ (or is undefined). Here, $\nabla f = \left \langle \answer {1-2x-y},\answer {1-2y-x} \right \rangle .$ The point where $\nabla f = \vec {0}$ is: $(\answer {1/3},\answer {1/3})$ . This point isis not in the region.
We have four boundary curves to check. Let’s check $x=0$ first. Plugging in $x = 0$ into the function gives $f(0,y) = \answer {y-y^2}$ and an interval for $y$ is: $[\answer {0}\answer {2}]$ . The derivative of this one variable function with respect to $y$ is: $f'(0,y) = \answer {1-2y}$ This is zero when $y = \answer {1/2}$ which means that $(0,\answer {1/2})$ is a critical point. We also have the endpoints, which gives two more points: $(0,0)$ and $(\answer {0},\answer {2})$ .
Now let’s look at a different boundary curve, say $y=2$ . Plugging $y=2$ into the function gives $f(x,2) = \answer {-x^2-x-2}.$ The derivative of this one variable function with respect to $x$ is $f'(x,2) = \answer {-2x-1},$ which is zero when $x = \answer {-1/2}$ . This gives a critical point $(\answer {-1/2},2)$ , which is not in the region, so we disregard it. Again, we take endpoints: $x=0$ and $x=2$ , which gives the two points $(0,2)$ and $(2,2)$ (notice $(0,2)$ is a repeat).
Repeat for the remaining two boundary curves. All critical points accumulated at the end are: $(1/3,1/3), (0,0), (0,2), (2,2), (2,0), (0,1/2), (\answer {1/2},\answer {0}).$
Plugging all these critical points into the function $f(x,y)$ shows there is a maximum value of: $\answer {1/3}$

Consider the function $f(x,y) = x^2+2y^2$ on the square $0 \leq x \leq 1$ , $0 \leq y \leq 1$ . The maximum value is: $\answer {3}$ , and the global minimum is: $\answer {0}$ .

Consider the function $f(x,y) = x^3+y^3-3xy$ on the square $0 \leq x \leq 1$ , $0 \leq y \leq 1$ . The maximum value is: $\answer {1}$ , and the global minimum is: $\answer {-1}$ .

Consider the function $f(x,y) = x^2-2xy+2y$ on the triangle given by $x \geq 0$ , $y \geq 0$ , $y \leq 2-x$ . The global maximum value is: $\answer {4}$ and the global minimum is: $\answer {0}$

Consider the function $f(x,y) = x^2y$ on the disc $x^2+y^2 \leq 3$ . The maximum value is: $\answer {2}$ and the global minimum is: $\answer {-2}$

True/False

If $f(x,y)$ is continuous and differentiable everywhere, and the global maximum and minimum of $f(x,y)$ on a region $R$ exist, then $R$ must be both closed and bounded. TrueFalse

The region $R: \, -\sqrt {1-x^2} \leq y < \sqrt {1-x^2}$ is bounded but not closed. TrueFalse

The function $f(x,y) = x+y$ has a global maximum value on the region $-x < y \leq -x+1$ . TrueFalse