- 1.
- Understand how double integrals give volumes.
- 2.
- Know what Fubini’s theorem says and why it works.
- 3.
- Be able to set up and compute double integrals over arbitrary regions in the -plane using Cartesian coordinates.
Recap Video
The following video recaps the ideas of the section.
_
To recap:
Given a function and a region in the -plane, the double integral
represents the signed volume under lying over the region in the
-plane.
Fubini’s Theorem The double integral of a continuous over a rectangle can
be computed as iterated integrals in either order ( or ):
Test your understanding with the following questions. The double integral
represents what?
The signed surface area of the solid under and over the
region The signed volume of the region under and over the region The unsigned surface area of the region under and over the region The unsigned volume of the region under and over the region
Example Video
Here is a video working through an example of setting up double integrals.
Problems
Double Integrals over Rectangles
Represent , where , as an integral in the order and , and then evaluate the
integral.
- In the order , we get (fill in the bounds)
- In the order , we get (fill in the bounds)
- Evaluate in either order to get
Double Integrals over General Regions
Method: To determine the bounds for the iterated integrals over regions that aren’t rectangles, look at cross sections.
Set up the double integral , where is the region bounded by , , , in the order
, and then , and then evaluate the integral. 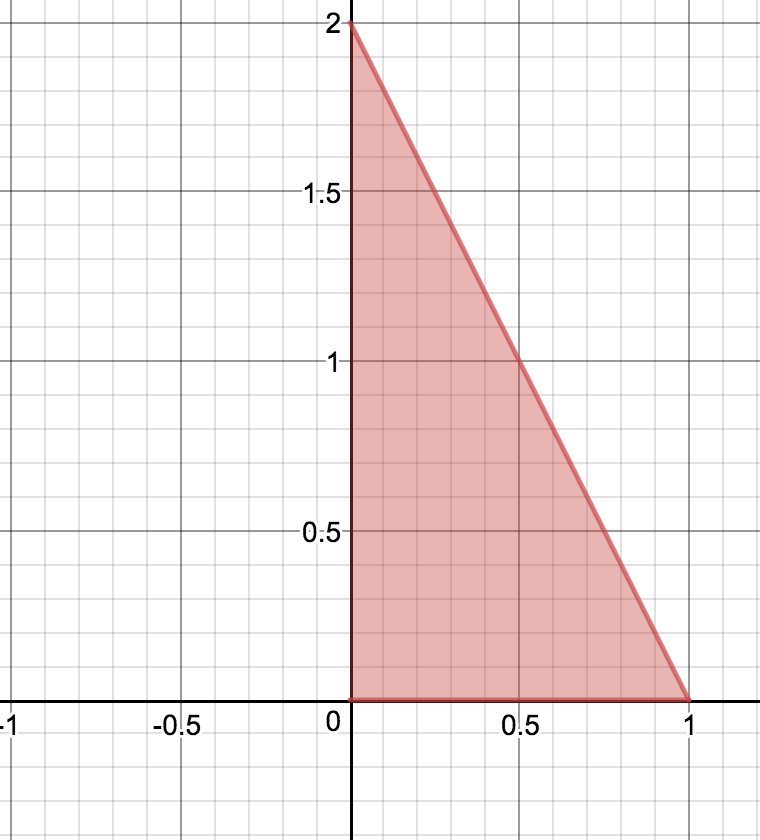

- In the order , the iterated integral bounds are:
- In the order , the iterated integral bounds are:
- The integral evaluates to
Set up the integral of a function over the region bounded by , , and in the
order and .
- In the order , the integral is
- In the order , the integral needs to be split up, and it is: