Double Integrals in Polar Coordinates

$\newenvironment {prompt}{}{} \newcommand {\DeclareMathOperator }[2]{\@OldDeclareMathOperator {##1}{##2}\immediate \write \myfile {\unexpanded {\DeclareMathOperator }{\unexpanded {##1}}{\unexpanded {##2}}}} \newcommand {\reserved@a }[2]{} \newcommand {\HyperFirstAtBeginDocument }[0]{\AtBeginDocument } \newcommand {\reserved@a }[1]{} \newcommand {\reserved@a }[2]{} \newcommand {\AppendGraphicsExtensions }[0]{\@ifundefined {Gin@extensions}{\let \Gin@extensions \@empty }{}\@ifstar {\grfext@Append \grfext@Check }{\grfext@Append \grfext@@Add }} \newcommand {\PrependGraphicsExtensions }[0]{\@ifundefined {Gin@extensions}{\let \Gin@extensions \@empty }{}\@ifstar {\grfext@Prepend \grfext@Check }{\grfext@Prepend \grfext@@Add }} \newcommand {\RemoveGraphicsExtensions }[1]{\@ifundefined {Gin@extensions}{\def \Gin@extensions {}}{\edef \grfext@tmp {\zap@space ##1 \@empty }\@for \grfext@ext :=\grfext@tmp \do {\def \grfext@next {\let \grfext@tmp \Gin@extensions \@expandtwoargs \@removeelement \grfext@ext \Gin@extensions \Gin@extensions \ifx \grfext@tmp \Gin@extensions \let \grfext@next \relax \fi \grfext@next }\grfext@next }}\grfext@Print \RemoveGraphicsExtensions } \newcommand {\epstopdfsetup }[0]{\setkeys {ETE}} \newcommand {\epstopdfcall }[1]{\ifETE@InsideSetfile \expandafter \@firstoftwo \else \expandafter \@secondoftwo \fi {‘##1}{\Gin@base \Gin@ext }} \newcommand {\epstopdfDeclareGraphicsRule }[4]{\ifx \\##4\\\@PackageError {epstopdf-base}{Conversion command is missing}\@ehc \else \begingroup \@ifundefined {Gin@rule@##1}{}{\@PackageInfo {epstopdf-base}{Redefining graphics rule for ‘##1’}}\endgroup \@namedef {Gin@rule@##1}####1{{##2}{##3}{\epstopdfcall {##4}}}\fi } \newcommand {\GetTitleStringSetup }[0]{\setkeys {gettitlestring}} \newcommand {\GetTitleString }[0]{\ifGTS@expand \expandafter \GetTitleStringExpand \else \expandafter \GetTitleStringNonExpand \fi } \newcommand {\GetTitleStringExpand }[1]{\def \GetTitleStringResult {##1}\begingroup \GTS@DisablePredefinedCmds \GTS@DisableHook \edef \x {\endgroup \noexpand \def \noexpand \GetTitleStringResult {\GetTitleStringResult }}\x } \newcommand {\GetTitleStringNonExpand }[1]{\def \GetTitleStringResult {##1}\global \let \GTS@GlobalString \GetTitleStringResult \begingroup \GTS@RemoveLeft \GTS@RemoveRight \endgroup \let \GetTitleStringResult \GTS@GlobalString } \newcommand {\GTS@DisableHook }[0]{} \newcommand {\label@hook }[0]{} \newcommand {\@currentlabelname }[0]{} \newcommand {\reserved@a }[0]{} \newcommand {\@safe@activestrue }[0]{} \newcommand {\@safe@activesfalse }[0]{} \newcommand {\nameref }[0]{\@ifstar \T@nameref \T@nameref } \newcommand {\Sectionformat }[2]{##1} \newcommand {\vnameref }[1]{\unskip ~\nameref {##1}\@vpageref [\unskip ]{##1}} \newcommand {\ref }[0]{\@ifstar \@refstar \T@ref } \newcommand {\pageref }[0]{\@ifstar \@pagerefstar \T@pageref } \newcommand {\nameref }[0]{\@ifstar \@namerefstar \T@nameref } \newcommand {\reserved@a }[2]{} \newcommand {\reserved@a }[0]{\AtBeginDocument } \newcommand {\reserved@a }[1]{} \newcommand {\reserved@a }[2]{}$

Objectives:

1.: Be comfortable working in polar coordinates.
2.: Know how to transform a double integral in Cartesian coordinates into a double integral in polar coordinates.
3.: Understand what the scaling factor is when moving to polar coordinates.

Recap Video

The following video recaps the ideas of the section.

To recap:

Suppose $f(x,y)$ is a function, and $R$ is a region in the $xy$ -plane corresponding to a region $D$ in polar coordinates. Then $\iint _R f(x,y)dA = \iint _D f(r\cos (\theta ),r\sin (\theta ))r dr\,d\theta .$

Example Video

Below is a video working through an example of double integrals in polar coordinates.

If $D$ is the region $x^2+y^2 \leq 4$ , $y \geq 1$ , evaluate $\iint _D ydA.$

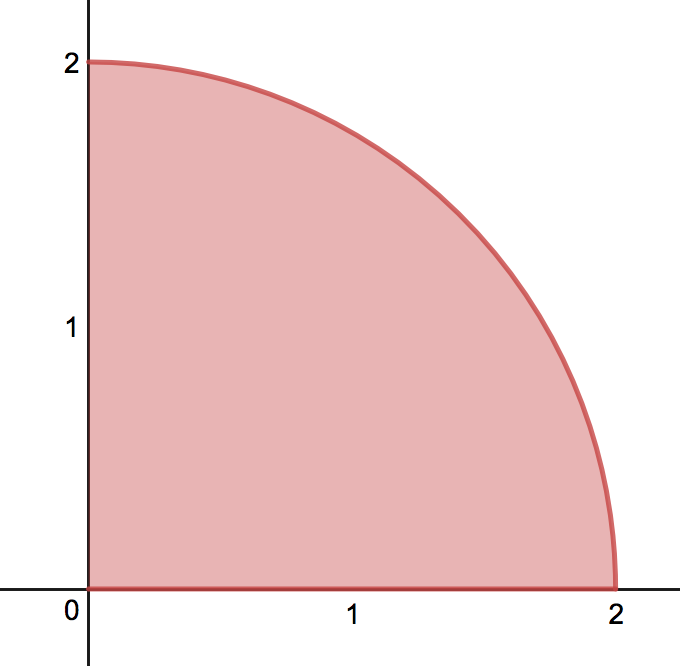
Compute the integral of $f(x,y) = x+y$ over the region $R$ which is the portion of $x^2+y^2 \leq 4$ in the first quadrant using polar coordinates.

Steps:

Draw the region. The region looks like:
Write the integrand $f(x,y)$ in polar coordinates: $f(r\cos (\theta ),r\sin (\theta )) = \answer {r\cos (\theta )+r\sin (\theta )}$
The region $R$ in polar coordinates can be described as: $\answer {0} \leq r \leq \answer {2} \quad \quad \quad \text { and } \quad \quad \quad 0 \leq \theta \leq \answer {\pi /2}$
The double integral in polar is therefore: $\iint _R f(x,y)dA = \int _{\answer {0}}^{\answer {\pi /2}} \int _{\answer {0}}^{\answer {2}} \answer {(r\cos (\theta )+r\sin (\theta ))r} dr\,d\theta .$
Evaluate the integral to get: $\answer {\frac {16}{3}}$

Compute the integral of $f(x,y) = x$ over the region bounded by $y = \sqrt {1-x^2}$ , $y=x$ , and $y=-x$ .

Again, draw the region, which is shown in the figure.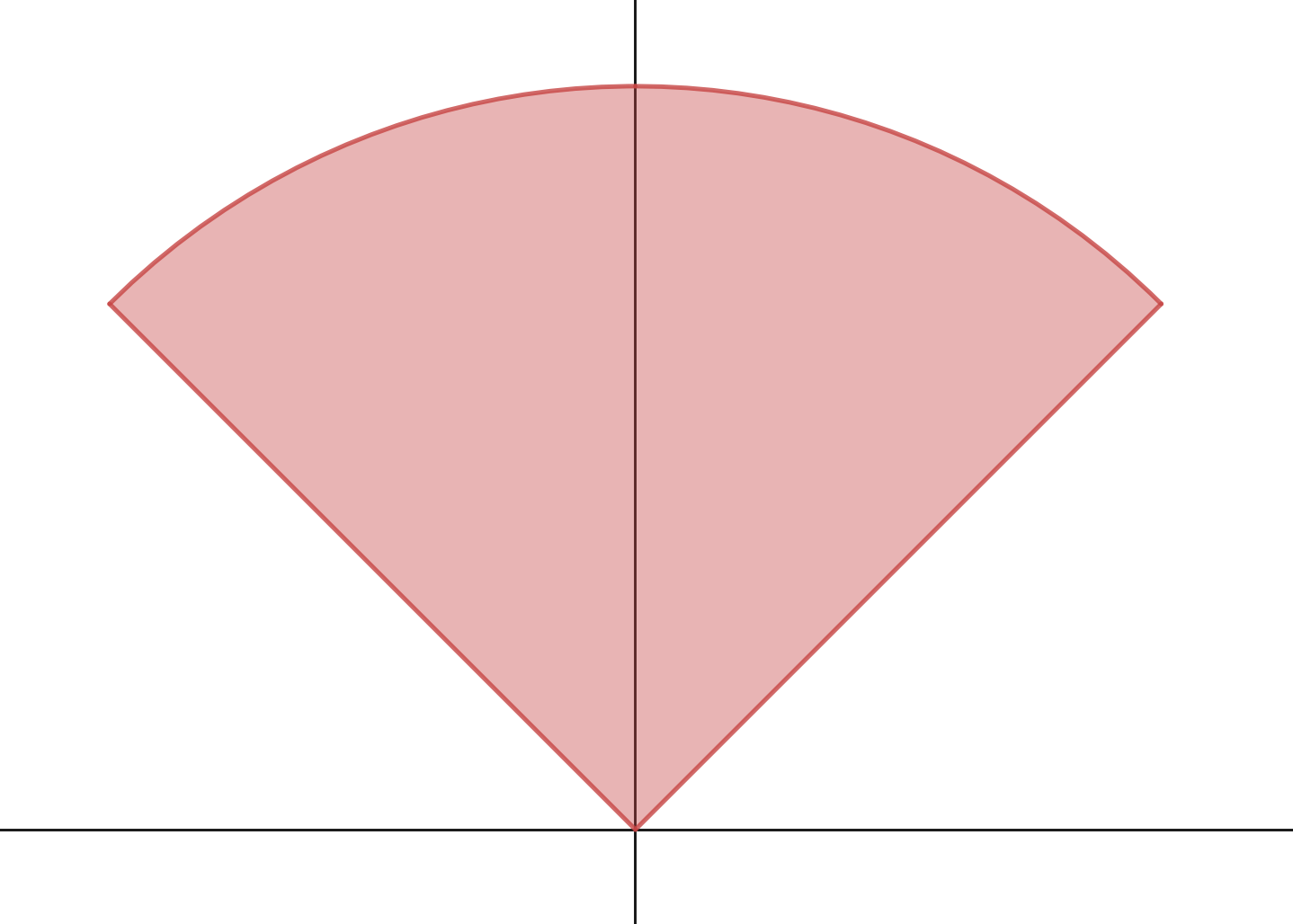

After drawing the region:

Transform the integrand. In polar, $f(r\cos (\theta ),r\sin (\theta )) = \answer {r\cos (\theta )}.$
Figure out the bounds for $r$ and $\theta$ . Again, drawing rays out from the origin, we see $r$ goes from the origin to the outer circle, which has polar equation $r=1$ . Therefore $\answer {0} \leq r \leq \answer {1}.$ Also note that $\theta$ goes from the line $y=x$ to the line $y=-x$ . The line $y=x$ has polar equation $\theta = \answer {\pi /4}$ (give answer between $0$ and $2\pi )$ , and the line $y=-x$ has polar equation $\theta =\answer {3\pi /4}$ .
The setup of the double integral in polar coordinates should be: $\int _{\answer {\pi /4}}^{\answer {3\pi /4}} \int _{\answer {0}}^{\answer {1}} \answer {r^2\cos (\theta )} dr\,d\theta .$
Evaluating this integral, we get: $\answer {0}$

Compute the integral of $f(x,y) = \frac {1}{\sqrt {x^2+y^2}}$ over the region inside the circle of radius $1$ centered at $(1,0)$ .

The setup of the double integral in polar coordinates is: $\int _{\answer {-\pi /2}}^{\pi /2} \int _{\answer {0}}^{\answer {2\cos (\theta )}} \answer {1} dr\,d\theta .$ This integral evaluates to: $\answer {4}$

Compute the area of the region outside $x^2+y^2=1$ and inside $x^2+(y-1)^2=1$ .

The graph of the region is shown below.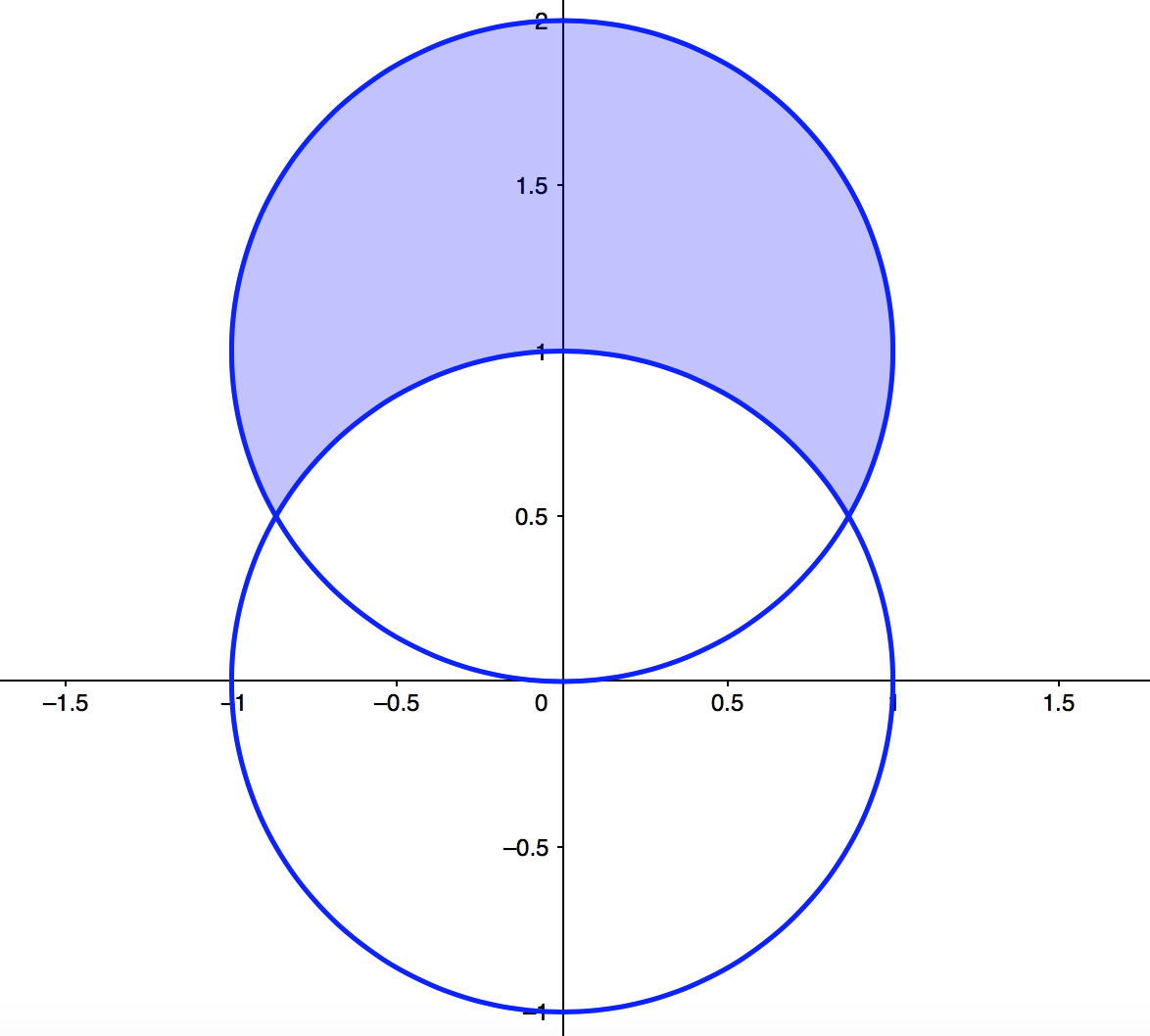

To get the area, we want to integrate $f(x,y) = \answer {1}$ , which in polar is $f(r\cos (\theta ),r\sin (\theta )) = \answer {1}.$ To get the bounds for $r$ and $\theta$ , first draw rays from the origin outward. Notice that they enter the region at the circle $x^2+y^2=1$ , which has polar equation $r= \answer {1}$ , and the leave the region at the circle $x^2+(y-1)^2=1$ , which has polar equation $r = \answer {2\sin (\theta )}$ . This gives us the $r$ bounds. To get $\theta$ , notice that $\theta$ will sweep between the two intersection points of the two circles. They intersect when $r = 2\sin (\theta )$ intersects $r=1$ , so when $2\sin (\theta ) = 1$ . This gives the values $\theta = \pi /6$ and $\theta = \answer {5\pi /6}$ . Therefore, the setup for the double integral is $\int _{\pi /6}^{\answer {5\pi /6}} \int _{\answer {1}}^{\answer {2\sin (\theta )}} \answer {r}dr\,d\theta .$ This evaluates to $\answer {\frac {\sqrt {3}}{2}+\frac {\pi }{3}}$ .

Set up the following double integral in polar coordinates: $\displaystyle \int _0^1 \int _x^{\sqrt {3}x}x dy\,dx$ .
The integral becomes: $\int _{\answer {\pi /4}}^{\answer {\pi /3}} \int _{\answer {0}}^{\answer {\sec (\theta )}}\answer {r^2 \cos (\theta )}dr\,d\theta .$

Find the volume of the solid inside $x^2+y^2=1$ bounded above by $z=x$ and below by the $xy$ -plane.

If we are going to evaluate this as a double integral $\iint _R f(x,y)dA$ , we want to let $f(x,y) = \answer {x}$ . The region in the $xy$ -plane we want is the portion of $x^2+y^2 \leq 1$ where $x \geq \answer {0}$ , which can be described in polar as: $\answer {0} \leq r \leq \answer {1} \quad \quad \quad \text { and } \quad \quad \quad \answer {-\pi /2} \leq \theta \leq \answer {\pi /2}$ The double integral therefore becomes: $\int _{\answer {-\pi /2}}^{\answer {\pi /2}} \int _{\answer {0}}^{\answer {1}} \answer {r^2\cos (\theta )} dr d\theta ,$ which evaluates to: $\answer {2/3}$