Exploring the Gradient Properties

$\newenvironment {prompt}{}{} \newcommand {\DeclareMathOperator }[2]{\@OldDeclareMathOperator {##1}{##2}\immediate \write \myfile {\unexpanded {\DeclareMathOperator }{\unexpanded {##1}}{\unexpanded {##2}}}} \newcommand {\reserved@a }[2]{} \newcommand {\HyperFirstAtBeginDocument }[0]{\AtBeginDocument } \newcommand {\reserved@a }[1]{} \newcommand {\reserved@a }[2]{} \newcommand {\AppendGraphicsExtensions }[0]{\@ifundefined {Gin@extensions}{\let \Gin@extensions \@empty }{}\@ifstar {\grfext@Append \grfext@Check }{\grfext@Append \grfext@@Add }} \newcommand {\PrependGraphicsExtensions }[0]{\@ifundefined {Gin@extensions}{\let \Gin@extensions \@empty }{}\@ifstar {\grfext@Prepend \grfext@Check }{\grfext@Prepend \grfext@@Add }} \newcommand {\RemoveGraphicsExtensions }[1]{\@ifundefined {Gin@extensions}{\def \Gin@extensions {}}{\edef \grfext@tmp {\zap@space ##1 \@empty }\@for \grfext@ext :=\grfext@tmp \do {\def \grfext@next {\let \grfext@tmp \Gin@extensions \@expandtwoargs \@removeelement \grfext@ext \Gin@extensions \Gin@extensions \ifx \grfext@tmp \Gin@extensions \let \grfext@next \relax \fi \grfext@next }\grfext@next }}\grfext@Print \RemoveGraphicsExtensions } \newcommand {\epstopdfsetup }[0]{\setkeys {ETE}} \newcommand {\epstopdfcall }[1]{\ifETE@InsideSetfile \expandafter \@firstoftwo \else \expandafter \@secondoftwo \fi {‘##1}{\Gin@base \Gin@ext }} \newcommand {\epstopdfDeclareGraphicsRule }[4]{\ifx \\##4\\\@PackageError {epstopdf-base}{Conversion command is missing}\@ehc \else \begingroup \@ifundefined {Gin@rule@##1}{}{\@PackageInfo {epstopdf-base}{Redefining graphics rule for ‘##1’}}\endgroup \@namedef {Gin@rule@##1}####1{{##2}{##3}{\epstopdfcall {##4}}}\fi } \newcommand {\GetTitleStringSetup }[0]{\setkeys {gettitlestring}} \newcommand {\GetTitleString }[0]{\ifGTS@expand \expandafter \GetTitleStringExpand \else \expandafter \GetTitleStringNonExpand \fi } \newcommand {\GetTitleStringExpand }[1]{\def \GetTitleStringResult {##1}\begingroup \GTS@DisablePredefinedCmds \GTS@DisableHook \edef \x {\endgroup \noexpand \def \noexpand \GetTitleStringResult {\GetTitleStringResult }}\x } \newcommand {\GetTitleStringNonExpand }[1]{\def \GetTitleStringResult {##1}\global \let \GTS@GlobalString \GetTitleStringResult \begingroup \GTS@RemoveLeft \GTS@RemoveRight \endgroup \let \GetTitleStringResult \GTS@GlobalString } \newcommand {\GTS@DisableHook }[0]{} \newcommand {\label@hook }[0]{} \newcommand {\@currentlabelname }[0]{} \newcommand {\reserved@a }[0]{} \newcommand {\@safe@activestrue }[0]{} \newcommand {\@safe@activesfalse }[0]{} \newcommand {\nameref }[0]{\@ifstar \T@nameref \T@nameref } \newcommand {\Sectionformat }[2]{##1} \newcommand {\vnameref }[1]{\unskip ~\nameref {##1}\@vpageref [\unskip ]{##1}} \newcommand {\ref }[0]{\@ifstar \@refstar \T@ref } \newcommand {\pageref }[0]{\@ifstar \@pagerefstar \T@pageref } \newcommand {\nameref }[0]{\@ifstar \@namerefstar \T@nameref } \newcommand {\reserved@a }[2]{} \newcommand {\reserved@a }[0]{\AtBeginDocument } \newcommand {\reserved@a }[1]{} \newcommand {\reserved@a }[2]{}$

Gradient is Perpendicular to Level Curves

The following is a contour map for a function $z = f(x,y)$ . We will examine why at any point $P(a,b)$ , the gradient $\nabla f(P)$ has to be perpendicular to the (tangent to the) level curve.

Everything below refers to this contour map. We can parametrize the level curve passing through $P$ , call it $\textbf {r}(t)$ . Assume $P$ corresponds to $t=0$ .

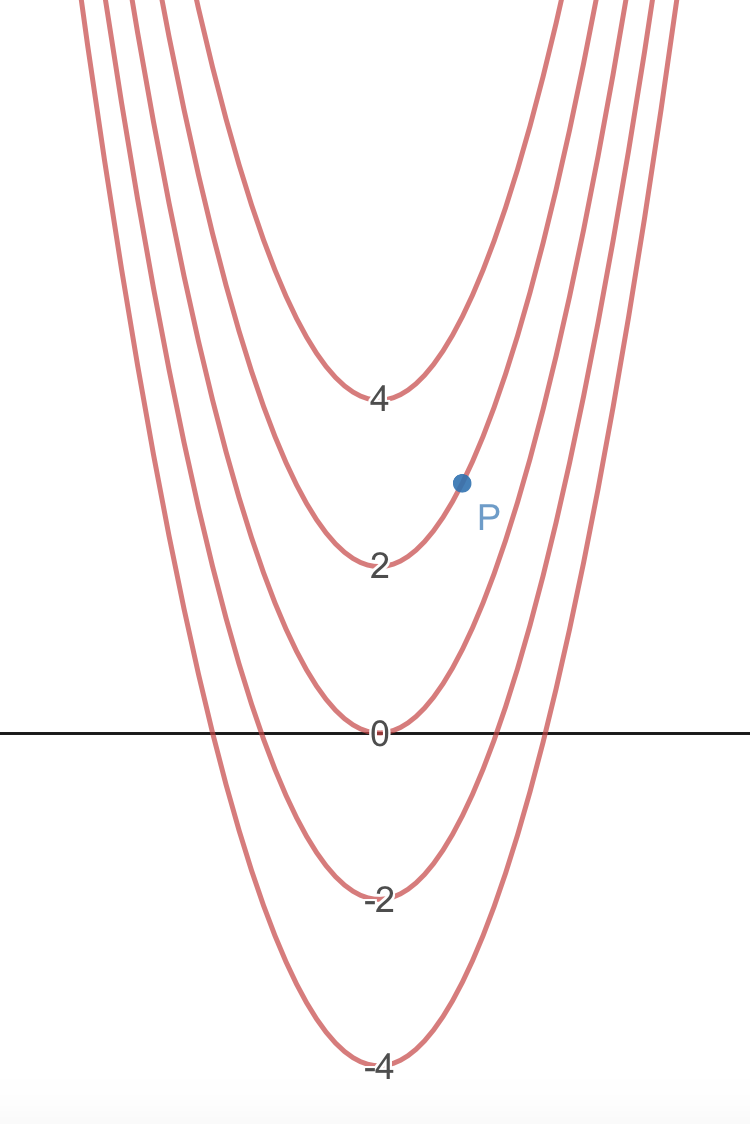
Since $\textbf {r}(t)$ represents the level curve through $P$ , we know that $f(\textbf {r}(t))$ is constant, which means $f(\textbf {r}(t)) = \answer {2}.$
Since $f(\textbf {r}(t))$ is constant, we know $\frac {d}{dt}f(\textbf {r}(t)) = \answer {0}$ .
By the chain rule, $\frac {d}{dt}f(\textbf {r}(t)) = \nabla f(\textbf {r}(t)) \cdot \textbf {r}'(t).$
The point $P$ corresponds to $t=0$ , so we can plug in $t=0$ to get $\nabla f(P) \cdot \textbf {r}'(0) = 0.$
What does $\textbf {r}'(0)$ represent?
The vector from the origin to $P$ . A tangent vector to the curve at $P$ . A vector perpendicular to the curve at $P$ .
Since the dot product is $0$ , we know that $\nabla f(P)$ and $\textbf {r}'(0)$ are parallelperpendicular .

Therefore, $\nabla f(P)$ is perpendicular to the tangent to the level curve.

Gradient Points in the Direction of Maximum Increase

Now we will see why the gradient points in the direction of maximum increase. This means of all vectors $\textbf {u}$ , the one which gives a maximum value of $D_{\textbf {u}}f(P)$ is $\textbf {u} = \nabla f(P)$ . It all comes down to the formula $D_{\textbf {u}}f(P) = \nabla f(P) \cdot \hat {\textbf {u}}.$

By the cosine formula for the dot product, which of the following is equal to $D_{\textbf {u}}f(P)$ ?
$\| \nabla f(P) \| \| \textbf {u} \| \cos (\theta )$ , where $\theta$ is the angle between $\nabla f(P)$ and $\textbf {u}$ . $\| \nabla f(P) \| \cos (\theta )$ , where $\theta$ is the angle between $\nabla f(P)$ and $\textbf {u}$ .
Since $0 \leq \theta \leq \pi$ , the maximum value of $D_{\textbf {u}}f(P)$ happens when $\theta = \answer {0}$ .
This means that $\nabla f(P)$ and $\textbf {u}$ have what relationship?
They point in the same direction. They are perpendicular. They point in opposite directions.

Therefore, the maximum rate of change happens in the direction of $\nabla f(P)$ .

The Magnitude of the Gradient Is the Maximum Rate of Increase

The last thing we will consider is why $\| \nabla f(P) \|$ is the maximum rate of increase at the point $P$ . Again it boils down to $D_{\textbf {u}}f(P) = \nabla f(P) \cdot \hat {\textbf {u}} = \| \nabla f(P) \| \cos (\theta ).$ We saw in the previous section that the maximum value of $D_{\textbf {u}}f(P)$ happens when $\theta = \answer {0}$ , or when $\textbf {u}$ points in the same direction as $\nabla f(P)$ . If $\theta = 0$ , then $\cos (\theta ) = \answer {1}$ , so in this case, $D_{\textbf {u}}f(P) = \| \nabla f(P) \| \cos (0) = \| \nabla f(P)\| ,$ which is exactly what we wanted.