Now that we’ve talked about what measurement gives us and how to think about units of measure, we’re ready to do some measuring. Quite a bit of this content is related to the ideas of dimension, so it’s a good idea to refresh yourself on that content by re-reading the section or looking back over your notes again before moving forward.

We should start by talking about what we mean by length, area, and volume.

The process of measurement

We will think about measuring length, area, or volume as a four step process.

1.

Choose an aspect to measure and describe it specifically.

2.

Choose an appropriate unit for measuring and describe it specifically.

3.

Iterate your unit all over the object, leaving no gaps and no overlaps.

4.

Report and interpret your results.

We discussed the first two steps here in the previous section. Remember that describing things specifically is key to making a good measurement, and your descriptions should make it clear what dimension you’re working in. Also remember that an appropriate unit is one that is the same dimension as the aspect you are measuring.

The word “iterate” in step 3 might feel a little strange here, but the goal is to again see that the process of measuring is the same for length, area, or volume. If we are measuring length, we might say “line up the unit end-to-end” instead of saying “iterate”. If we are measuring area, we might say “cover the object with the unit” instead of using “iterate”. And if we are measuring volume, we might say “fill the object with units” instead of talking about iterating. Please use vocabulary that makes sense to you and to the situation!

In the previous section, we talked about measuring a golf club using a golf pencil. Let’s return to this example to talk about how we would actually make this measurement.

First, we choose an aspect to measure. In this case it’s the length area volume of the golf club. We could also draw a picture of the golf club and indicate on our picture what we mean by the length to make things even more clear.

Next, we choose a unit of measure. In this case it’s the length area volume of the golf pencil. We know this unit of measure is appropriate for this measurement because both the aspect we are measuring and the unit we are using are 1D 2D 3D . We could again draw and label a picture of our unit if we found that helpful, but we’ll skip it for this example.

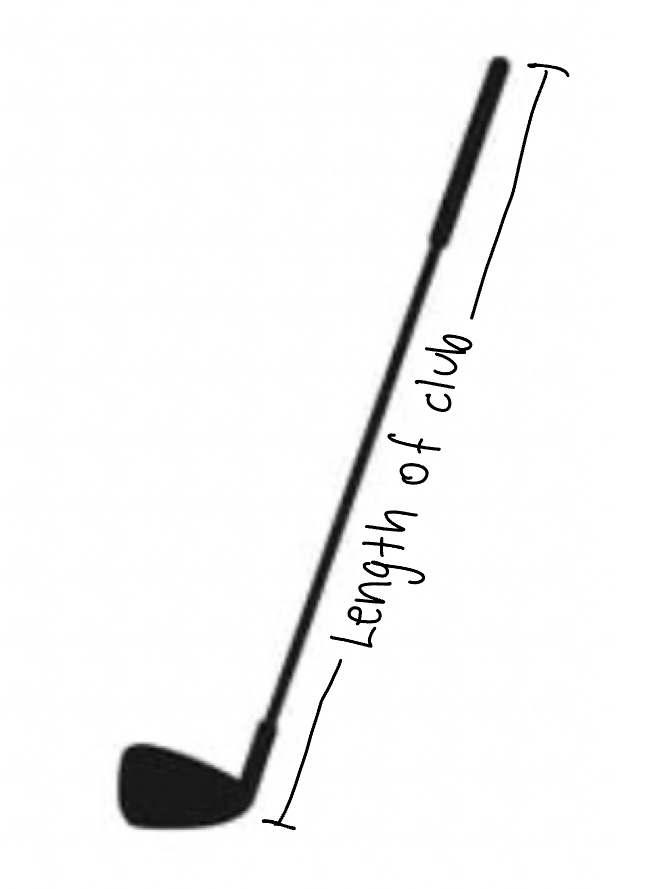
Our third step is to iterate the unit all over the object, leaving no gaps and no overlaps. In this case we want to cover up the entire length of the golf club with pencils. So, we start at one end of the golf club and line up our unit. We then line up the next unit with the end of the first unit, leaving no gaps and no overlaps. We keep using the same unit of measure, so we don’t turn the pencil sideways. We keep repeating this process until we have accounted for the entire length of the golf club. We include a drawing of our process below.

For our fourth step, we report and interpret our results. In this case it looks like we used $5\frac {1}{3}$ pencils to cover up the entire length of the golf club. To be really precise, we would have to make sure that last pencil is cut into three equal pieces! This means that our answer is that the length of the golf club is $\answer [given]{5+\frac {1}{3}}$ pencil lengths. Our answer means that if we think of the length of the pencil as one unit, the length of the golf club is $5 \frac 13$ times as much as that original unit, or that it takes $5 \frac 13$ copies of our unit to make up the 1D space that the length of the club takes up. Remember, that’s what it means to be a length of something!

Let’s pause here and return to number lines. Perhaps you can see a nice connection between units of measure, number lines, and rulers. We build number lines by choosing a location for zero and a unit of length, and then we make a bunch of copies of that unit of measure to represent our whole numbers.

Using the number line below, what is the length of the line $L$ which starts at zero and ends at the mark labeled $6$?

The length of the line is $\answer {6}$ units.

What is the length of the line $L$ which starts at the mark labeled two and ends at the mark labeled $6$?

The length of the line is $\answer {4}$ units.

However, the number line is actually more powerful than to only be used as a ruler. The number line allows us to connect our ideas about length to our general ideas about numbers. For instance, the idea of the number “two” can refer to two units of length, but it can also refer to two candy bars or two dogs or two friends. All of these ideas about “two” are different, but they all can be represented by counting the number of units we need to move from zero on a number line. From using a number line to understand whole numbers, we can also understand fractions by cutting our units into equal-sized pieces. And from there, we can even define irrational numbers using their locations on the number line! We have a nice way of representing all kinds of numbers that even helps us understand what it means for one number to be larger or smaller than another!

Approximate measurements

Notice that in the previous section, we actually gave an approximate answer to the length example, because we estimated that the last pencil was about $\frac 13$ of a full pencil’s length. This is because in order to approximate length, area, or volume, we follow essentially the same four-step process for measurement that we do in order to get an exact measurement. The main difference is that when we approximate, it’s okay to have gaps or overlaps, and it’s okay to count too much or too little area. The closer we want our approximation to be, however, the less often we should leave those gaps, overlaps, or extra space.

Estimate the area inside the shape below.

For our process of measurement, we would like to measure the area inside the shape, and area is the amount of 2D space that the object takes up. Since the object is on top of a grid, we will use the area of one grid square as our unit. The area of the grid square is 1D 2D 3D , and so is the area we are trying to measure, so this unit is appropriate to use.

To estimate the area, the most basic thing we could do would be to count the number of grid squares inside the shape. To find an exact area, we would have to leave no gaps and no overlaps, but to estimate we don’t have to be quite as precise. So, for instance, one strategy we could use would be to count only the squares that are fully inside the shape. I counted $45$ squares inside the shape. How many did you count? $\answer [tolerance=8]{45}$

We now report and interpret our answer. Since I counted $45$ squares inside the shape, I would answer that the shape’s area is approximately $45$ squares. If you counted a different number, your answer would be different than mine, and that’s perfectly fine in this case! My answer means that the amount of 2D space inside the shape is approximately the same as $45$ copies of the 2D space inside my unit. My estimate here is probably an over estimate (too big) an under estimate (too small) because I didn’t account for all of the space inside the shape.

In the example above, we used the grid squares as our area unit, and grid squares are often convenient units to use. In fact, units that are square are so convenient, we give them a special name.

Returning to estimation, notice that we don’t need to use square units to make our estimates. In fact, there’s a game some people play where they try to estimate the number of candies in a jar. Usually the point of this game is that the person whose estimate is closest to the actual number of candies wins the whole jar. This game is really just about estimating the amount of 3D space inside the jar using the candies.

When we think about estimation, we should also consider how much precision we need for the situation at hand. Think about how certain division problems that don’t have exact answers can ask for different types of answers. For instance, if we calculate $38 \div 5$, sometimes we give an exact answer, sometimes we round up, sometimes we round down, and so on. When we approximate, the problem could ask for an overestimate or an underestimate, or we could be asked to round to the nearest whole number of squares or even the nearest $5$ squares. Pay attention to the context of a story problem as much as you pay attention to whether you are overestimating or underestimating. You may also need to pay attention to significant figures when rounding.

Hallie needs to cover the shape below with square tiles. The tiles come in packages of 10, and can be cut up to be used in her project. How many packages should Hallie buy?

For this example, I counted approximately $45$ squares covering the object. Note that your count could be different than mine! How many boxes of tiles should Hallie buy? Hallie should buy $\answer {5}$ boxes of tiles.

Since Hallie can only buy the tiles in packages of $10$, we need to round up to the nearest multiple of 10, which would be $50$ tiles. Then $50$ tiles would correspond to $5$ boxes of tiles.

Moving and additivity

As we begin to work with measuring, one of the first things we want to kids to recognize and use concerning length, area, and volume is that they are additive. We can write this down formally as follows.

This should almost feel like common sense, but it’s a powerful technique that we want kids to both use and recognize when they are using. So, in our explanations we’d like to point out when we are using this principle.

Javier has a bucket that has $40$ cubic centimeters of sand in it, and Damien has a bucket that has $50$ cubic centimeters of sand in it. If the kids both dump their buckets of sand into a larger, empty bucket, how much sand will be in the larger bucket?

$\answer [given]{90}$ cubic centimeters of sand

Javier and Damien start out with their individual buckets of sand, and then they dump them out and combine them together into a single bucket.

Our goal is to combine the amount of 3D space in the first bucket with the amount of 3D space in the second bucket, and combining is an action that we recognize as meaning we use the addition subtraction multiplication division operation. We don’t gain or lose sand in this process, so we just use our chosen operation.

Notice that we can also use the additivity principle “backwards”: if we start with a total amount of length, area, or volume, and then remove some to get back to a part of the total amount, we would typically use subtraction to model what is happening with our length, area, or volume. If you’d like, you can refer to this as a “subtractitivity principle”, but it’s really the same idea as the additivity principle. As usual, the exact terminology matters less than a detailed description of what’s happening and why it’s happening in your explanation!

Haven has a piece of rope which measures $4$ meters total. Then they cut off a piece of the rope which measures $2.5$ meters. How much rope is left after the cutting?

In our picture, we marked off the cut at $2.5$ meters. We could write an equation that corresponds to this situation by writing the following. \[ 2.5 + ? = 4 \] So, we can see the additivity principle at work. The $2.5$ meter piece and the unknown piece together make up the entire $4$ meter piece. We combine those two pieces together to get the whole, and so we can combine their lengths to get the length of the whole. We don’t gain or lose any length when we put these pieces together.

To get the unknown by itself, we could remove the 2.5 meter piece from the $4$ meter piece, and the removing is an action we recognize as meaning we use the addition subtraction multiplication division operation. This means our final answer for the length of the unknown part is $\answer [given]{1.5}$ meters.

The other principle that helps us to find lengths, areas, and volumes is called the moving principle.

We can use the moving principle to rearrange the L-shape below into another shape whose area might be easier to find.

We can cut off the bottom part of the L and move it to the top part of the L. If we attach it with no gaps and no overlaps, we will still have the same amount of area that we started with according to the moving principle.

In the image, the dashed line shows where the extra piece from the bottom was attached to the bigger piece, forming a rectangle which is $5$ squares wide and $2$ squares tall. We can count the squares in either figure to verify that the area hasn’t changed: in each figure we have $\answer [given]{10}$ squares of area in total.

As with the additivity principle, stating the moving principle by name generally isn’t necessary. But your explanations should make it clear what you are doing with the length, area, or volume and why you expect that it didn’t change. It’s very important that you don’t introduce any gaps or overlaps while you move pieces around! Sometimes we will work to show that the pieces fit exactly as they are supposed to, and sometimes it’s okay to just state that the pieces fit exactly. We will practice both types of explanations, and we will be clear which type of explanation we are asking for on any problem you solve.

Shearing

There is a special case of the moving principle that we would like to highlight called shearing. Let’s consider an example before we make our definition.

Start with a rectangle.

Cut the rectangle into a bunch of thin strips.

The moving principle says if we move around these strips without creating any gaps or overlaps, we haven’t changed the area of the shape. One of the strips is highlighted yellow so that you can see how it moves. In order to not create any gaps or overlaps, the way we want to move the strips is to keep one of them right where it is, and slide all of the rest of them parallel to the one that isn’t moving. There are lots of ways to do this, but here is one example.

Here is the tricky part. Imagine cutting those little strips thinner and thinner and thinner, until they are so thin you can’t even see them (and then thinner still)! Here’s an example with thinner strips so you can see what’s happening.

(There are so many little strips here that the computer has to skip one of them. But just imagine it’s there with all of the others!) As we cut more and more, the jagged sides of this shape are getting more and more smooth. So, if we imagine that we could cut the strips so thin we couldn’t cut them anymore (we might call this infinitesimally thin but the terminology isn’t too important), we would have a parallelogram instead of a rectangle.

This parallelogram is one result of shearing the rectangle. When you draw your own examples of shearing, please highlight what is happening to at least one of the strips as they move around.

To summarize, here are the steps for shearing.

1.

Choose a base that will not move when you do the shearing.

2.

Cut the object into small strips parallel to the chosen base.

3.

Shift the strips parallel to the chosen base.

4.

Imagine cutting the strips so thin that the sides smooth out.

The part about cutting the strips so thin that the sides smooth out is perhaps a bit fuzzy, and a mathematician named Bonaventura Cavalieri who lived in the early 1600s would have agreed with you. But he studied this idea and came up with what we now call Cavalieri’s Principle, which says that even when you cut into strips so thin you can’t see them anymore, or even if you could cut into infinitely many strips, you don’t change the area of the shape by this process. Cavalieri proved that this is true, and so we know it’s still true today. In fact, Cavalieri’s Principle was one of the early steps towards calculus!

Finally, notice that we practiced shearing with an area in our example, but you can also use this technique of shearing on a 3D object.

More vocabulary

As we wrap up this section, we want to bring to your attention two pieces of vocabulary that connect lengths, areas, and volumes.

Notice that perimeter is 1D while area is 2D. This is a very important distinction that we talked a little bit about when we first began thinking about dimension. A perimeter is a length, while the shape itself has an area. This is a connection between length and area, but because both measurements can be taken on the same shape, the distinction between perimeter and area can be tough for some people.

We will work with these ideas more as we move forward, but never hesitate to start a conversation if you are confused!