Local and Global Error Bounds

$\newenvironment {prompt}{}{} \newcommand {\Sec }[2]{\section {#1}} \newcommand {\trademark }[0]{{R\!\!\!\!\!\bigcirc }} \newcommand {\EXER }[0]{\section *{Exercises}} \newcommand {\CEXER }[0]{} \newcommand {\TEXER }[0]{} \newcommand {\R }[0]{\mbox {$\Bbb {R}$}} \newcommand {\C }[0]{\mbox {$\Bbb {C}$}} \newcommand {\Z }[0]{\mbox {$\Bbb {Z}$}} \newcommand {\N }[0]{\mbox {$\Bbb {N}$}} \newcommand {\D }[0]{\mbox {{\bf D}}} \newcommand {\setmin }[0]{\;\mbox {--}\;} \newcommand {\Matlab }[0]{{M\small {AT\-LAB}} } \newcommand {\Matlabp }[0]{{M\small {AT\-LAB}}} \newcommand {\computer }[0]{\Matlab Instructions} \newcommand {\half }[0]{\mbox {$\frac {1}{2}$}} \newcommand {\compose }[0]{\raisebox {.15ex}{\mbox {{\scriptsize $\circ $}}}} \newcommand {\AND }[0]{\quad \mbox {and}\quad } \newcommand {\vect }[2]{\left (\begin {array}{c} #1_1 \\ \vdots \\ #1_{#2}\end {array}\right )} \newcommand {\mattwo }[4]{\left (\begin {array}{rr} #1 & #2\\ #3 &#4\end {array}\right )} \newcommand {\mattwoc }[4]{\left (\begin {array}{cc} #1 & #2\\ #3 &#4\end {array}\right )} \newcommand {\vectwo }[2]{\left (\begin {array}{r} #1 \\ #2\end {array}\right )} \newcommand {\vectwoc }[2]{\left (\begin {array}{c} #1 \\ #2\end {array}\right )} \newcommand {\inv }[0]{^{-1}} \newcommand {\CC }[0]{{\cal C}} \newcommand {\CCone }[0]{\CC ^1} \newcommand {\Span }[0]{{\rm span}} \newcommand {\rank }[0]{{\rm rank}} \newcommand {\trace }[0]{{\rm tr}} \newcommand {\RE }[0]{{\rm Re}} \newcommand {\IM }[0]{{\rm Im}} \newcommand {\nulls }[0]{{\rm null\;space}} \newcommand {\dps }[0]{\displaystyle } \newcommand {\arraystart }[0]{\renewcommand {\arraystretch }{1.8}} \newcommand {\arrayfinish }[0]{\renewcommand {\arraystretch }{1.2}} \newcommand {\Start }[1]{\vspace {0.08in}\noindent {\bf Section~\ref {#1}}} \newcommand {\exer }[1]{\noindent {\bf \ref {#1}}} \newcommand {\ans }[0]{} \newcommand {\matthree }[9]{\left (\begin {array}{rrr} #1 & #2 & #3 \\ #4 & #5 & #6 \\ #7 & #8 & #9\end {array}\right )} \newcommand {\cvectwo }[2]{\left (\begin {array}{c} #1 \\ #2\end {array}\right )} \newcommand {\cmatthree }[9]{\left (\begin {array}{ccc} #1 & #2 & #3 \\ #4 & #5 & #6 \\ #7 & #8 & #9\end {array}\right )} \newcommand {\vecthree }[3]{\left (\begin {array}{r} #1 \\ #2 \\ #3\end {array}\right )} \newcommand {\cvecthree }[3]{\left (\begin {array}{c} #1 \\ #2 \\ #3\end {array}\right )} \newcommand {\cmattwo }[4]{\left (\begin {array}{cc} #1 & #2\\ #3 &#4\end {array}\right )} \newcommand {\thehelp }[0]{\thesection .\arabic {equation}} \newcommand {\matlabEquation }[0]{\let \oldtheequation \theequation \renewcommand {\theequation }{\oldtheequation *}\begin {equation}} \newcommand {\HyperFirstAtBeginDocument }[0]{\AtBeginDocument } \newcommand {\epstopdfsetup }[0]{\setkeys {ETE}} changed the theorem header of amsthm failed\MessageBreak }}} \newcommand {\GetTitleStringSetup }[0]{\setkeys {gettitlestring}} \newcommand {\Sectionformat }[2]{#1} \newcommand {\arraystretch }[0]{1.8} \newcommand {\arraystretch }[0]{1.2}$ $% This file was *autogenerated* from localAndGlobalErrorBounds.sagetex.sage with % sagetex.py version 2015/08/26 v3.0-92d9f7a %52abb95817cd76612781d612683a0b89% md5sum of corresponding .sage file (minus "goboom","current_tex_line",and pause/unpause lines)$

We now want to analyze the error of a numerical method applied to an initial value problem of the form

$\begin{eqnarray*} \frac{dx}{dt} & = & f(t,x)\\ x(t_0) & = & x_0. \end{eqnarray*}$

Before introducing the general concept, we recall the crucial points in the error analysis that we have performed in Section ??.

Error Analysis From Section ??

We introduced two different types of error: the local discretization error $\delta (k)$ and the global discretization error $\epsilon (k)$ .

For Euler’s method, the local error is bounded by $\delta (k)\le \delta _h \le C_E h^2,$ where $C_E >0$ is a constant depending on the length of the interval $[0,T]$ on which the solution is approximated, see (??). (For example, $C_E =e^T/2$ .) In particular, on the interval $[0,T]$ , the local error goes to zero at least as fast as a quadratic function in the step size $h$ .

For Euler’s method the global error is bounded by $|\epsilon (k)|\le Dh,$ with a constant $D>0$ that again just depends on $T$ , see (??). Hence the global error tends to zero at least as fast as a linear function in the step size $h$ . Roughly speaking, one power is lost going from the local to the global error, and this power is lost while going through the estimate in (??). The same phenomenon occurs in the general error analysis.

A General Form for a Numerical Method

Let $x(t)$ be the solution of the initial value problem. From now on we represent an explicit numerical method by a function $\Phi$ as follows: for $k=0,1,\ldots ,K-1$ we have $t_k=t_0 + kh$ , $x_0 = x(t_0)$ , and $x_{k+1} = x_k + h\Phi (t_k,x_k,h).$

In Euler’s method (??) $\Phi (t_k,x_k,h)=f(t_k,x_k).$ In particular, in this case, $\Phi$ does not depend on the step size $h$ . In the modified Euler method (??) $\Phi (t_k,x_k,h) = \frac {1}{2} \Big ( f(t_k, x_k)+f(t_k+h, x_k + h f(t_k, x_k))\Big ).$

A General Form for Errors

Next we introduce the two different types of error for a numerical method given by $\Phi$ .

The local discretization error $\delta (k+1)$ is defined as $\delta (k+1) = x(t_{k+1}) - (x(t_k) + h\Phi (t_k,x(t_k),h)),$ where $k=0,1,\ldots ,K-1$ .
The global discretization error $\epsilon (k)$ is given by $\epsilon (k) = x(t_k)-x_k,$ where $k=0,1,\ldots ,K$ .

A Theorem on Global Discretization Errors

The purpose is to find a bound on the global error by the same technique as in Section ??. For this we need two assumptions:

In the error estimates for Euler’s method it was very convenient to use a bound for the local error that is independent of the actual step $k$ . Hence we assume that there is a constant $\delta _h>0$ such that $\begin{equation} \label{eq:locerrbound} |\delta(k+1)| \le \delta_h \quad \mbox{for all $k=0,1,\ldots,K-1$.} \end{equation}$ In concrete examples this fact can be guaranteed by the differentiability of the right hand side $f$ in the initial value problem.
We also need an additional assumption on the function $\Phi$ : we assume that there is a constant $L>0$ such that for all $t,h,y,z$ $\begin{equation} \label{eq:PhiLip} |\Phi(t,y,h)-\Phi(t,z,h)|\le L|y-z|. \end{equation}$ For Euler’s method $\Phi (t,x,h)=f(t,x)$ and therefore (??) is satisfied if $f$ is (globally) Lipschitz continuous in $x$ .

We are now in the position to derive a bound for the global discretization error proceeding completely analogous to Section ??. Observe that by Definition ??(a) $x(t_k) = x(t_{k-1}) + h\Phi (t_{k-1},x(t_{k-1}),h)+\delta (k).$ On the other hand, the numerical method can be written as $x_k = x_{k-1} + h\Phi (t_{k-1},x_{k-1},h).$ Subtracting these two equations from each other and using (??), (??) we obtain

$\begin{eqnarray*} |\epsilon(k)| &=& |x(t_k)-x_k|\\ &=& |x(t_{k-1})-x_{k-1} + h[\Phi(t_{k-1},x(t_{k-1}),h)- \Phi(t_{k-1},x_{k-1},h)] +\delta(k)|\\ &\le& |x(t_{k-1})-x_{k-1}|+hL|x(t_{k-1})-x_{k-1}|+|\delta(k)|\\ &\le& (1+hL)|x(t_{k-1})-x_{k-1}|+\delta_h\\ &=& (1+hL)|\epsilon(k-1)|+\delta_h. \end{eqnarray*}$

This inequality is of the same type as the inequality in first line in (??) — one just has to replace the first $h$ by $hL$ . Hence we can repeat the estimate in (??) and obtain $|\epsilon (k)| \le \frac {(1+hL)^k -1}{hL}\delta _h.$ Since $1+hL\le e^{hL}$ we have proved the following result.

Suppose that (??) and (??) hold. Then the global discretization error of the numerical method given by the function $\Phi$ satisfies $\begin{equation} \label{eq:geestimate} |\epsilon(k)| \le \left(\frac{e^{khL}-1}{L}\right)\frac{\delta_h}{h}. \end{equation}$

An Example Using Euler’s Method

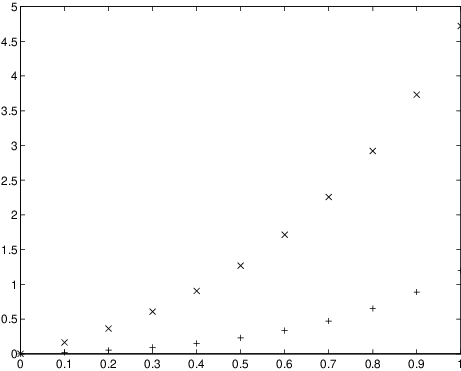
The estimate (??) indicates that the constant $L$ plays an important role for the size of the global discretization error. Indeed, let us illustrate this fact by applying Euler’s method to the initial value problem

$\begin{equation} \label{exam:Lchange} \begin{array}{rcl} \dps\frac{dx}{dt} & = & \lambda x\\ x(0) & = & 1, \end{array} \end{equation}$ on the interval $[0,T]$ . In this case $L=\lambda$ since for Euler’s method $|\Phi (t,y,h)-\Phi (t,z,h)|=|f(t,y)-f(t,z)|=|\lambda y-\lambda z|=\lambda |y-z|.$ Moreover, since we know the exact solution we may compute $\delta _h$ for this case as follows: we have $\delta (k+1) = e^{\lambda t_{k+1}} - (e^{\lambda t_k} + \lambda h e^{\lambda t_k}) = e^{\lambda kh}(e^{\lambda h}-(1+\lambda h)),$ and since $e^{\lambda h}-(1+\lambda h)\le e^{\lambda h}\frac {(\lambda h)^2}{2}$ we obtain (see also (??)) $\delta (k+1)\le e^{\lambda kh} e^{\lambda h}\frac {(\lambda h)^2}{2}\le e^{\lambda T}\frac {(\lambda h)^2}{2}.$ Therefore we can choose $\begin{equation} \label{eq:dhlam} \delta_h = \lambda^2 e^{\lambda T} \frac{h^2}{2}. \end{equation}$ In fact, observe that for $\lambda =1$ we recover (??).

Proceeding as in Section ?? we set $\lambda =2$ and compute the global discretization error and its bound in (??) by MATLAB on the interval $[0,1]$ for the step size $h=0.1$ . Concretely we type

h      = 0.1;
 
L      = 2;
 
t(1)   = 0;
 
x(1)   = 1;
 
err(1) = 0;
 
est(1) = 0;
 
K      = 1/h;
 
for k = 1:K
 
     t(k+1) = t(k)+h;
                                                                  

                                                                  
 
     x(k+1) = (1+L*h)*x(k);
 
   err(k+1) = exp(L*t(k+1))-x(k+1);
 
   est(k+1) = exp(L)*(exp(L*k*h)-1)*L*h/2;
 
end
 
plot(t,err,’+’)
 
hold on
 
plot(t,est,’x’)

The result is shown in Figure ??. A comparison with Figure ?? shows that the error is indeed significantly bigger reflecting the fact that here $L=2$ whereas in the example in Section ?? this constant was one.

Figure 1: The global discretization error (marked by $+$ ) and its bound given in (??) (marked by $\times$ ) for the step size $h=0.1$ .

A Bound on Local Discretization Errors

It remains to demonstrate how to determine a bound $\delta _h$ on the local discretization error $\delta (k)$ for a given numerical method applied to the initial value problem

$\begin{eqnarray*} \frac{dx}{dt} & = & f(t,x)\\ x(t_0) & = & x_0, \end{eqnarray*}$

on the interval $[t_0,t_e]$ . Again we consider Euler’s method. The crucial tool for the computation of the local error is a Taylor expansion of the solution combined with the fact that the derivatives of $x(t)$ can be written in terms of the function $f$ by the differential equation. Using this idea we expand $x(t_{k+1})=x(t_k+h)$ up to second order by

$\begin{eqnarray*} x(t_{k+1})&=& x(t_k)+h\frac{dx}{dt}(t_k)+\frac{h^2}{2}\frac{d^2x}{dt^2}(t_k+\theta h)\\ &=& x(t_k)+hf(t_k,x(t_k))+\frac{h^2}{2}\frac{d^2x}{dt^2}(t_k+\theta h), \end{eqnarray*}$

with an appropriate $0<\theta <1$ . Substitution into the expression for the local error leads to

$\begin{eqnarray*} \delta(k+1)&=&x(t_{k+1}) - (x(t_k) + hf(t_k,x(t_k)))\\ &=& \frac{h^2}{2}\frac{d^2x}{dt^2}(t_k+\theta h). \end{eqnarray*}$

Hence, choosing a constant $C_E$ by $C_E=\frac {1}{2} \max \left \{ \left \vert \frac {d^2x}{dt^2}(s)\right \vert ,\, t_0\le s\le t_e\right \},$ we find that $\delta (k+1)\le \delta _h$ for all $k$ if we set $\delta _h = C_E h^2.$

Since the solution $x(t)$ of the initial value problem is in general not known, it is more appropriate to find a bound for the constant $C_E$ directly from the right hand side $f$ in the differential equation. We now outline a procedure how this can be accomplished.

We have $\frac {dx}{dt}(t)=f(t,x(t))$ and it follows

$\begin{equation} \label{eq:Taylor2} \begin{array}{rcl} \dps\frac{d^2x}{dt^2}(t) &=& \dps\frac{\partial f}{\partial t}(t,x(t)) +\frac{\partial f}{\partial x}(t,x(t))\frac{dx}{dt}(t)\\ &=& \dps\frac{\partial f}{\partial t}(t,x(t)) +\frac{\partial f}{\partial x}(t,x(t))f(t,x(t)). \end{array} \end{equation}$ Hence if a solution has to be computed for $t_0\le t\le t_e$ , and the values of the solution certainly are in the range $x_\ell \le x \le x_u$ , then $\begin{equation} \label{eq:CE} C_E\le \frac{1}{2}\max\left\{ \left\vert\frac{\partial f}{\partial t}(s,y) +\frac{\partial f}{\partial x}(s,y)f(s,y)\right\vert,\, t_0\le s\le t_e,\quad x_\ell \le y \le x_u \right\}. \end{equation}$

As an example of (??) we approximate the solution of the initial value problem

$\begin{eqnarray*} \frac{dx}{dt} & = & 5 x\\ x(0) & = & 1, \end{eqnarray*}$

on the interval $[0,T]$ . Here $f(t,x)=5 x$ and therefore $\frac {\partial f}{\partial t}(t,x)=0\AND \frac {\partial f}{\partial x}(t,x)=5.$ From the ODE we see that the solution is monotonically increasing and thus we find that $C_E\le \frac {1}{2}\max \left \{ \left \vert 0+5\cdot 5y\right \vert , y=x(T) \right \} = \frac {25}{2}x(T).$ Therefore we can choose $\delta _h = \frac {25}{2}\bar x h^2$ for any $\bar x$ such that $\bar x \ge x(T)$ . In particular, we have confirmed the result we have previously obtained, see (??).

The computation of the local discretization error using Taylor expansions is quite tedious. Therefore we just remark here that for the modified Euler method the local error can be bounded by a function of the form $\delta _h = C_Mh^3,$ and for the fourth order Runge-Kutta method the local discretization error is bounded by $\delta _h = C_R h^5.$ Here $C_M$ and $C_R$ are positive constants.

A Bound on Global Discretization Errors

Once the local discretization error is bounded we can use Theorem ?? to obtain a bound on global discretization error. In particular, we can prove:

Suppose that (??) holds. Then there are constants $C_E$ , $C_M$ and $C_R$ such that the global discretization error of

Euler’s method is bounded by $|\epsilon (k)| \le \frac {e^{khL}-1}{L}C_E h;$
the modified Euler method is bounded by $|\epsilon (k)| \le \frac {e^{khL}-1}{L}C_M h^2;$
the fourth order Runge-Kutta method is bounded by $|\epsilon (k)| \le \frac {e^{khL}-1}{L}C_R h^4.$

In view of this proposition it is clear that the fourth order Runge-Kutta method is much better than Euler’s method or the modified Euler method: the reason is that for small step sizes $h$ the value of $h^4$ is much smaller than $h^2$ or even $h$ itself. Hence the global discretization error of the fourth order Runge-Kutta method is, for reasonably small step sizes, much smaller than for the other two methods. In addition, it is also evident how the fourth order Runge-Kutta method got its name.

Specifying the Tolerance

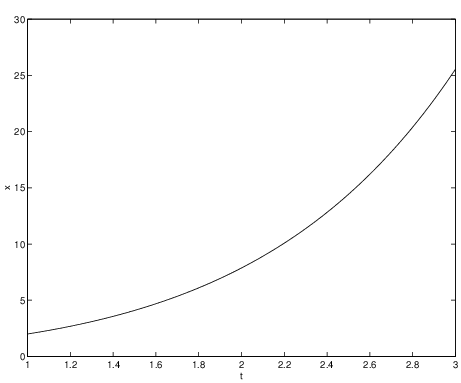
In principle, we can use Proposition ?? to find a step size for which the global discretization error is not bigger than a specified tolerance. To illustrate this point, consider the initial value problem (see also (??))

$\begin{eqnarray*} \frac{dx}{dt} & = & x+t \\ x(1) & = & 2. \end{eqnarray*}$

The aim is to find a step size $h$ such that Euler’s method is approximating the solution on the interval $[1,3]$ up to a global discretization error smaller than $0.1$ . By Proposition ?? this can be guaranteed if $h$ is chosen so that $\frac {e^{khL}-1}{L}C_E h < 0.1.$ For this example $L=1$ , since $|y+t-(z+t)|=|y-z|=1\cdot |y-z|.$

We now find a bound for the constant $C_E$ . We compute $\frac {\partial f}{\partial t}(s,y)=\frac {\partial f}{\partial x}(s,y)=1.$ We see from the ODE that the solution is monotonically increasing. Suppose that we know that for $t\in [1,3]$ the solution $x(t)$ is bounded by $40$ from above. Using (??) we obtain an estimate for $C_E$ by $C_E\le \frac {1}{2}\max \left \{\vert 1+1\cdot f(s,y)\vert ,\, 1\le s\le 3,\, 2 \le y \le 40 \right \}=\frac {44}{2}=22.$ Since $e^{kh}\le e^{t_e-t_0}=e^2$ , we can choose an $h$ such that $(e^2-1)22h < 0.1\quad \Longleftrightarrow \quad h<\frac {1}{220(e^2-1)}\approx 0.00071.$ Indeed, computing a solution with MATLAB by

h     = 0.0007;
 
t(1)  = 1;
 
x(1)  = 2;
 
K     = round(2/h);
 
for k = 1:K
 
     t(k+1) = t(k)+h;
 
     x(k+1) = x(k)+h*(x(k)+t(k));
 
end
 
plot(t,x)
 
xlabel(’t’)
 
ylabel(’x’)

we obtain the result in Figure ??. (The MATLAB command round rounds a number towards the nearest integer.) The outcome cannot be distinguished from the exact solution shown in Figure ??(b).

Figure 2: The numerical solution obtained by Euler’s method for the step size $h=0.0007$ .

Exercises

Determine the function $\Phi =\Phi (t_k,x_k,h)$ which belongs to the fourth order Runge-Kutta method.

In Exercises ?? – ?? find an estimate for the constant $C_E$ of the form $C_E \le Kx(t_0)$ where $x(t)$ is the solution of the specified initial value problem on $[0,T]$ and $t_0\in [0,T]$ .

$\dps \frac {dx}{dt} = 3 x$ where $x(0) = 2$ .

$\dps \frac {dx}{dt} = -x$ where $x(0) = 1$ .

Set $\lambda =0.2$ and the step size $h=0.1$ . Use MATLAB to compute the global discretization error and its bound in (??) on the interval $[0,1]$ . Compare the result with the ones obtained in Figures ?? and ??.