The Initial Value Problem

$\newenvironment {prompt}{}{} \newcommand {\Sec }[2]{\section {#1}} \newcommand {\trademark }[0]{{R\!\!\!\!\!\bigcirc }} \newcommand {\EXER }[0]{\section *{Exercises}} \newcommand {\CEXER }[0]{} \newcommand {\TEXER }[0]{} \newcommand {\R }[0]{\mbox {$\Bbb {R}$}} \newcommand {\C }[0]{\mbox {$\Bbb {C}$}} \newcommand {\Z }[0]{\mbox {$\Bbb {Z}$}} \newcommand {\N }[0]{\mbox {$\Bbb {N}$}} \newcommand {\D }[0]{\mbox {{\bf D}}} \newcommand {\setmin }[0]{\;\mbox {--}\;} \newcommand {\Matlab }[0]{{M\small {AT\-LAB}} } \newcommand {\Matlabp }[0]{{M\small {AT\-LAB}}} \newcommand {\computer }[0]{\Matlab Instructions} \newcommand {\half }[0]{\mbox {$\frac {1}{2}$}} \newcommand {\compose }[0]{\raisebox {.15ex}{\mbox {{\scriptsize $\circ $}}}} \newcommand {\AND }[0]{\quad \mbox {and}\quad } \newcommand {\vect }[2]{\left (\begin {array}{c} #1_1 \\ \vdots \\ #1_{#2}\end {array}\right )} \newcommand {\mattwo }[4]{\left (\begin {array}{rr} #1 & #2\\ #3 &#4\end {array}\right )} \newcommand {\mattwoc }[4]{\left (\begin {array}{cc} #1 & #2\\ #3 &#4\end {array}\right )} \newcommand {\vectwo }[2]{\left (\begin {array}{r} #1 \\ #2\end {array}\right )} \newcommand {\vectwoc }[2]{\left (\begin {array}{c} #1 \\ #2\end {array}\right )} \newcommand {\inv }[0]{^{-1}} \newcommand {\CC }[0]{{\cal C}} \newcommand {\CCone }[0]{\CC ^1} \newcommand {\Span }[0]{{\rm span}} \newcommand {\rank }[0]{{\rm rank}} \newcommand {\trace }[0]{{\rm tr}} \newcommand {\RE }[0]{{\rm Re}} \newcommand {\IM }[0]{{\rm Im}} \newcommand {\nulls }[0]{{\rm null\;space}} \newcommand {\dps }[0]{\displaystyle } \newcommand {\arraystart }[0]{\renewcommand {\arraystretch }{1.8}} \newcommand {\arrayfinish }[0]{\renewcommand {\arraystretch }{1.2}} \newcommand {\Start }[1]{\vspace {0.08in}\noindent {\bf Section~\ref {#1}}} \newcommand {\exer }[1]{\noindent {\bf \ref {#1}}} \newcommand {\ans }[0]{} \newcommand {\matthree }[9]{\left (\begin {array}{rrr} #1 & #2 & #3 \\ #4 & #5 & #6 \\ #7 & #8 & #9\end {array}\right )} \newcommand {\cvectwo }[2]{\left (\begin {array}{c} #1 \\ #2\end {array}\right )} \newcommand {\cmatthree }[9]{\left (\begin {array}{ccc} #1 & #2 & #3 \\ #4 & #5 & #6 \\ #7 & #8 & #9\end {array}\right )} \newcommand {\vecthree }[3]{\left (\begin {array}{r} #1 \\ #2 \\ #3\end {array}\right )} \newcommand {\cvecthree }[3]{\left (\begin {array}{c} #1 \\ #2 \\ #3\end {array}\right )} \newcommand {\cmattwo }[4]{\left (\begin {array}{cc} #1 & #2\\ #3 &#4\end {array}\right )} \newcommand {\thehelp }[0]{\thesection .\arabic {equation}} \newcommand {\matlabEquation }[0]{\let \oldtheequation \theequation \renewcommand {\theequation }{\oldtheequation *}\begin {equation}} \newcommand {\HyperFirstAtBeginDocument }[0]{\AtBeginDocument } \newcommand {\epstopdfsetup }[0]{\setkeys {ETE}} changed the theorem header of amsthm failed\MessageBreak }}} \newcommand {\GetTitleStringSetup }[0]{\setkeys {gettitlestring}} \newcommand {\Sectionformat }[2]{#1} \newcommand {\arraystretch }[0]{1.8} \newcommand {\arraystretch }[0]{1.2} \newcommand {\arraystretch }[0]{1.8} \newcommand {\arraystretch }[0]{1.2}$ $% This file was *autogenerated* from theInitialValueProblem.sagetex.sage with % sagetex.py version 2015/08/26 v3.0-92d9f7a %07f8b09b317ae878d09b1232709baeb0% md5sum of corresponding .sage file (minus "goboom","current_tex_line",and pause/unpause lines)$

Recall that a planar autonomous system of ordinary differential equations has the form

$\begin{equation} \label{2dsystem} \begin{array}{ccl} \dps \frac{dx}{dt} & = & f(x,y) \\ \dps \frac{dy}{dt} & = & g(x,y). \end{array} \end{equation}$ Computer experiments using pplane5 always appear to find a unique solution to initial value problems. More precisely, we are led to believe that there is just one solution to (??) satisfying the initial conditions

$\begin{eqnarray*} x(0) & = & x_0 \\ y(0) & = & y_0. \end{eqnarray*}$

Existence and Uniqueness of Solutions

In fact, existence and uniqueness of solutions are not always guaranteed — though they are guaranteed for a large class of differential equations, as the following theorem shows.

Suppose that the functions $f$ and $g$ in the system of differential equations (??) are differentiable near $(x_0,y_0)$ and that the partial derivatives $f_x,f_y,g_x,g_y$ are continuous near $(x_0,y_0)$ . Then there exists a unique solution to (??) with initial conditions $(x(0),y(0))=(x_0,y_0)$ .

For example, consider the planar system of constant coefficient linear differential equations:

$\begin{equation} \label{2dlinsystem} \begin{array}{ccl} \dps \frac{dx}{dt} & = & ax+by \\ \dps \frac{dy}{dt} & = & cx+dy. \end{array} \end{equation}$ In (??), $f(x,y)=ax+by$ and $g(x,y)=cx+dy$ . The partial derivatives of $f$ and $g$ are easy to calculate; they are: $f_x=a$ , $f_y=b$ , $g_x=c$ , and $g_y=d$ . As constant functions, all of these partial derivatives are continuous. Hence, existence and uniqueness of solutions to the initial value problem for (??) are guaranteed by Theorem ??.

Although we have stated this theorem just for planar systems, the theorem itself is valid in all dimensions. For example, in one dimension the analog of Theorem ?? states that the differential equation $\dot {x} = f(x)$ with initial condition $x(0)=x_0$ has a unique solution $x(t)$ when $f'(x)$ exists and is continuous near $x_0$ .

A discussion of the proof of this theorem is beyond the scope of this text; nevertheless, the theorem is valid and we will use its consequences.

An Example of Nonuniqueness of Solutions

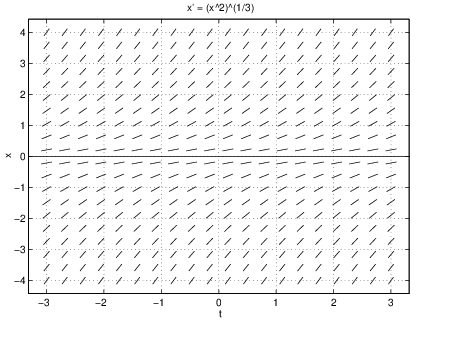
Indeed, uniqueness of solutions is not even guaranteed for single equations. Here is an example:

$\begin{equation} \label{nonunique} \frac{dx}{dt} = 3\sqrt[3]{x^2} = 3x^{2/3} \end{equation}$ with the initial condition $x(0)=0.$ Certainly the constant function $x(t)=0$ is a solution to (??) satisfying the initial value $x(0)=0$ . In addition, the function $x(t) = t^3$ is a solution to (??). This fact is checked by direct calculation: $\frac {dx}{dt} = 3t^2 \AND 3x^{2/3}= 3(t^3)^{2/3} = 3t^2.$

Example (??) shows that hypotheses like those in Theorem ?? are needed. Indeed, in (??) $f(x)=3x^{2/3} \AND f'(x) = \frac {2}{x^{1/3}}.$ Hence, $f$ is not differentiable at $x=0$ and the hypotheses of Theorem ?? fail.

At this point it is worth looking to see what dfield5 computes numerically. Start dfield5 and change the differential equation to:

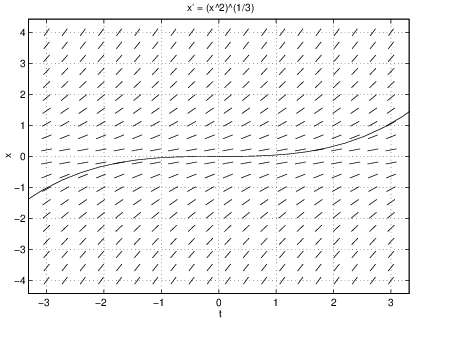
x’ = (x^2)^(1/3)

Writing the differential equation in this way guarantees that the computer will not compute square roots of negative numbers. Click on the Proceed button. In the DFIELD5 Display window attempt to click on the origin — that is, attempt to enter the initial condition $x(0)=0$ using the mouse. You will surely get a solution that has a similar shape to the graph of the cubic function $x=t^3$ . In the DFIELD5 Options menu click on Keyboard input, and in the DFIELD5 Keyboard input window enter the values $t=0$ and $x=0$ . After clicking on the Compute button you will see the solution $x=0$ . Now click on the Erase all solutions button in the DFIELD5 Options menu. Change the initial value of $x$ to $0.00001$ in the DFIELD5 Keyboard input window and click on Compute. You will see a solution that looks like $x=t^3$ . See Figure ??.

Figure 1: Solutions for (??) for $t\in [-3,3]$ and $x\in [-4,4]$ . Left: $x(0)=0$ . Right: $x(0)=0.00001$ .

At this stage, we do not have the background to discuss the numerical method employed by dfield5.

The Initial Value Problem for Linear Systems

In this chapter we discuss how to find solutions $(x(t),y(t))$ to (??) satisfying the initial values $x(0)=x_0$ and $y(0)=y_0$ . It is convenient to rewrite (??) in matrix form as:

$\begin{equation} \label{ndlinsystem} \frac{dX}{dt}(t) = CX(t). \end{equation}$ The initial value problem is then stated as: Find a solution to (??) satisfying $X(0)=X_0$ where $X_0=(x_0,y_0)^t$ . Everything that we have said here works equally well for $n$ dimensional systems of linear differential equations. Just let $C$ be an $n\times n$ matrix and let $X_0$ be an $n$ vector of initial conditions.

Solving the Initial Value Problem Using Superposition

In Section ?? we discussed how to solve (??) when the eigenvalues of $C$ are real and distinct. Recall that when $\lambda _1$ and $\lambda _2$ are distinct real eigenvalues of $C$ with associated eigenvectors $v_1$ and $v_2$ , there are two solutions to (??) given by the explicit formulas $X_1(t) = e^{\lambda _1 t}v_1 \AND X_2(t) = e^{\lambda _2 t}v_2.$ Superposition guarantees that every linear combination of these solutions $X(t) = \alpha _1X_1(t)+\alpha _2X_2(t) = \alpha _1e^{\lambda _1 t}v_1 + \alpha _2e^{\lambda _2 t}v_2$ is a solution to (??). In addition, we can always choose scalars $\alpha _1,\alpha _2\in \R$ to solve any given initial value problem of (??). It follows from the uniqueness of solutions to initial value problems stated in Theorem ?? that all solutions to (??) are included in this family of solutions.

We generalize this discussion so that we will be able to find closed form solutions to (??) in Section ?? when the eigenvalues of $C$ are complex or are real and equal.

Suppose that $X_1(t)$ and $X_2(t)$ are two solutions to (??) such that $v_1=X_1(0) \AND v_2=X_2(0)$ are linearly independent. The existence part of Theorem ?? guarantees that such solutions exist. Then all solutions to (??) are linear combinations of these two solutions. We verify this statement as follows. Corollary ?? of Chapter ?? states that since $\{v_1,v_2\}$ is a linearly independent set in $\R ^2$ , it is also a basis of $\R ^2$ . Thus for every $X_0\in \R ^2$ there exist scalars $r_1,r_2$ such that $X_0 = r_1v_1 + r_2v_2.$ It follows from superposition and Theorem ?? that the solution $X(t) = r_1X_1(t) + r_2X_2(t)$ is the unique solution whose initial condition vector is $X_0$ .

We have proved that every solution to this linear system of differential equations is a linear combination of these two solutions — that is, we have proved that the dimension of the space of solutions to (??) is two. This proof generalizes immediately to a proof of the following theorem for $n\times n$ systems.

Let $C$ be an $n\times n$ matrix. Suppose that $X_1(t),\ldots ,X_n(t)$ are solutions to $\dot {X}=CX$ such that the vectors of initial conditions $v_j=X_j(0)$ are linearly independent in $\R ^n$ . Then the unique solution to the system (??) with initial condition $X(0)=X_0$ is $\begin{equation} \label{E:genlsoln} X(t)=r_1X_1(t) + \cdots + r_nX_n(t), \end{equation}$ where $r_1,\ldots ,r_n$ are scalars satisfying $\begin{equation} \label{findscalars} X_0 = r_1v_1 + \cdots + r_nv_n. \end{equation}$

We call (??) the general solution to the system of differential equations $\dot {X}=CX$ . When solving the initial value problem we find a particular solution by specifying the scalars $r_1,\ldots ,r_n$ .

Let $C$ be an $n\times n$ matrix and let ${\cal X}=\{X_1(t),\ldots ,X_n(t)\}$ be solutions to the differential equation $\dot {X}=CX$ such that the vectors $X_j(0)$ are linearly independent in $\R ^n$ . Then the set of all solutions to $\dot {X}=CX$ is an $n$ -dimensional subspace of $(\CCone )^n$ , and $\cal X$ is a basis for the solution subspace.

Consider a special case of Theorem ??. Suppose that the matrix $C$ has $n$ linearly independent eigenvectors $v_1,\ldots ,v_n$ with real eigenvalues $\lambda _1,\ldots ,\lambda _n$ . Then the functions $X_j(t)=e^{\lambda _j t}v_j$ are solutions to $\dot {X}=CX$ . Corollary ?? implies that the functions $X_j$ form a basis for the space of solutions of this system of differential equations. Indeed, the general solution to (??) is

$\begin{equation} \label{e:gensoln} X(t) = r_1e^{\lambda_1 t}v_1 + \cdots + r_ne^{\lambda_n t}v_n. \end{equation}$ The particular solution that solves the initial value $X(0)=X_0$ is found by solving (??) for the scalars $r_1,\ldots ,r_n$ .

Exercises

In Exercises ?? – ??, consider the system of differential equations

$\begin{equation} \label{Ex.1.03} \begin{array}{rcr} \frac{dx}{dt} & = & 65x+42y \\ \frac{dy}{dt} & = & -99x-64y. \end{array} \end{equation}$

Verify that $v_1 = \vectwo {2}{-3} \AND v_2 = \vectwo {-7}{11}$ are eigenvectors of the coefficient matrix of (??) and find the associated eigenvalues.

Find the solution to (??) satisfying initial conditions $X(0) = (-14,22)^t$ .

Find the solution to (??) satisfying initial conditions $X(0) = (-3,5)^t$ .

Find the solution to (??) satisfying initial conditions $X(0) = (9,-14)^t$ .

In Exercises ?? – ??, consider the system of differential equations

$\begin{equation} \label{Ex.1.06} \begin{array}{rcr} \frac{dx}{dt} & = & x-y \\ \frac{dy}{dt} & = & -x+y. \end{array} \end{equation}$

The eigenvalues of the coefficient matrix of (??) are $0$ and $2$ . Find the associated eigenvectors.

Find the solution to (??) satisfying initial conditions $X(0)=(2,-2)^t$ .

Find the solution to (??) satisfying initial conditions $X(0)=(2,6)^t$ .

Find the solution to (??) satisfying initial conditions $X(0)=(1,0)^t$ .

In Exercises ?? – ??, consider the system of differential equations

$\begin{equation} \label{E:c6.1.1} \begin{array}{rcr} \frac{dx}{dt} & = & -y \\ \frac{dy}{dt} & = & x. \end{array} \end{equation}$

Show that $(x_1(t),y_1(t)) = (\cos t,\sin t)$ is a solution to (??).

Show that $(x_2(t),y_2(t)) = (-\sin t,\cos t)$ is a solution to (??).

Using Exercises ?? and ??, find a solution $(x(t),y(t))$ to (??) that satisfies $(x(0),y(0)) = (0,1)$ .

Using Exercises ?? and ??, find a solution $(x(t),y(t))$ to (??) that satisfies $(x(0),y(0)) = (1,1)$ .

In Exercises ?? – ??, consider the system of differential equations

$\begin{equation} \label{E:c6.1.2} \begin{array}{rcl} \frac{dx}{dt} & = & -2x+7y \\ \frac{dy}{dt} & = & 5y, \end{array} \end{equation}$

Find a solution to (??) satisfying the initial condition $(x(0),y(0)) = (1,0)$ .

Find a solution to (??) satisfying the initial condition $(x(0),y(0)) = (-1,2)$ .

In Exercises ?? – ??, consider the matrix $C = \left (\begin {array}{rrr} -1 & -10 & -6\\ 0 & 4 & 3 \\ 0 & -14 & -9 \end {array}\right ).$

Verify that $v_1 = \left (\begin {array}{r} 1 \\ 0\\ 0\end {array}\right ) \qquad v_2 = \left (\begin {array}{r} 2 \\ -1\\ 2\end {array}\right ) \quad \AND \quad v_3 = \left (\begin {array}{r} 6 \\ -3\\ 7\end {array}\right )$ are eigenvectors of $C$ and find the associated eigenvalues.

Find a solution to the system of differential equations $\dot {X}=CX$ satisfying the initial condition $X(0)= (10, -4, 9)^t$ .

Find a solution to the system of differential equations $\dot {X}=CX$ satisfying the initial condition $X(0)= ( 2, -1, 3)^t$ .

Show that for some nonzero $a$ the function $x(t)=at^5$ is a solution to the differential equation $\dot {x}=x^{4/5}$ . Then show that there are at least two solutions to the initial value problem $x(0)=0$ for this differential equation.

Use pplane5 to investigate the system of differential equations $\begin{equation} \label{Ex.1.4} \begin{array}{rcr} \frac{dx}{dt} & = & -2y \\ \frac{dy}{dt} & = & -x+y. \end{array} \end{equation}$

Use pplane5 to find two independent eigendirections (and hence eigenvectors) for (??).
Using (a), find the eigenvalues of the coefficient matrix of (??).
Find a closed form solution to (??) satisfying the initial condition $X(0) = \vectwo {4}{-1}.$
Study the time series of $y$ versus $t$ for the solution in (c) by comparing the graph of the closed form solution obtained in (c) with the time series graph using pplane5.