Periodic Forcing and Resonance

$\newenvironment {prompt}{}{} \newcommand {\Sec }[2]{\section {#1}} \newcommand {\trademark }[0]{{R\!\!\!\!\!\bigcirc }} \newcommand {\EXER }[0]{\section *{Exercises}} \newcommand {\CEXER }[0]{} \newcommand {\TEXER }[0]{} \newcommand {\R }[0]{\mbox {$\Bbb {R}$}} \newcommand {\C }[0]{\mbox {$\Bbb {C}$}} \newcommand {\Z }[0]{\mbox {$\Bbb {Z}$}} \newcommand {\N }[0]{\mbox {$\Bbb {N}$}} \newcommand {\D }[0]{\mbox {{\bf D}}} \newcommand {\setmin }[0]{\;\mbox {--}\;} \newcommand {\Matlab }[0]{{M\small {AT\-LAB}} } \newcommand {\Matlabp }[0]{{M\small {AT\-LAB}}} \newcommand {\computer }[0]{\Matlab Instructions} \newcommand {\half }[0]{\mbox {$\frac {1}{2}$}} \newcommand {\compose }[0]{\raisebox {.15ex}{\mbox {{\scriptsize $\circ $}}}} \newcommand {\AND }[0]{\quad \mbox {and}\quad } \newcommand {\vect }[2]{\left (\begin {array}{c} #1_1 \\ \vdots \\ #1_{#2}\end {array}\right )} \newcommand {\mattwo }[4]{\left (\begin {array}{rr} #1 & #2\\ #3 &#4\end {array}\right )} \newcommand {\mattwoc }[4]{\left (\begin {array}{cc} #1 & #2\\ #3 &#4\end {array}\right )} \newcommand {\vectwo }[2]{\left (\begin {array}{r} #1 \\ #2\end {array}\right )} \newcommand {\vectwoc }[2]{\left (\begin {array}{c} #1 \\ #2\end {array}\right )} \newcommand {\inv }[0]{^{-1}} \newcommand {\CC }[0]{{\cal C}} \newcommand {\CCone }[0]{\CC ^1} \newcommand {\Span }[0]{{\rm span}} \newcommand {\rank }[0]{{\rm rank}} \newcommand {\trace }[0]{{\rm tr}} \newcommand {\RE }[0]{{\rm Re}} \newcommand {\IM }[0]{{\rm Im}} \newcommand {\nulls }[0]{{\rm null\;space}} \newcommand {\dps }[0]{\displaystyle } \newcommand {\arraystart }[0]{\renewcommand {\arraystretch }{1.8}} \newcommand {\arrayfinish }[0]{\renewcommand {\arraystretch }{1.2}} \newcommand {\Start }[1]{\vspace {0.08in}\noindent {\bf Section~\ref {#1}}} \newcommand {\exer }[1]{\noindent {\bf \ref {#1}}} \newcommand {\ans }[0]{} \newcommand {\matthree }[9]{\left (\begin {array}{rrr} #1 & #2 & #3 \\ #4 & #5 & #6 \\ #7 & #8 & #9\end {array}\right )} \newcommand {\cvectwo }[2]{\left (\begin {array}{c} #1 \\ #2\end {array}\right )} \newcommand {\cmatthree }[9]{\left (\begin {array}{ccc} #1 & #2 & #3 \\ #4 & #5 & #6 \\ #7 & #8 & #9\end {array}\right )} \newcommand {\vecthree }[3]{\left (\begin {array}{r} #1 \\ #2 \\ #3\end {array}\right )} \newcommand {\cvecthree }[3]{\left (\begin {array}{c} #1 \\ #2 \\ #3\end {array}\right )} \newcommand {\cmattwo }[4]{\left (\begin {array}{cc} #1 & #2\\ #3 &#4\end {array}\right )} \newcommand {\thehelp }[0]{\thesection .\arabic {equation}} \newcommand {\matlabEquation }[0]{\let \oldtheequation \theequation \renewcommand {\theequation }{\oldtheequation *}\begin {equation}} \newcommand {\HyperFirstAtBeginDocument }[0]{\AtBeginDocument } \newcommand {\epstopdfsetup }[0]{\setkeys {ETE}} changed the theorem header of amsthm failed\MessageBreak }}} \newcommand {\GetTitleStringSetup }[0]{\setkeys {gettitlestring}} \newcommand {\Sectionformat }[2]{#1} \newcommand {\arraystretch }[0]{1.8} \newcommand {\arraystretch }[0]{1.2}$ $% This file was *autogenerated* from periodicForcingAndResonance.sagetex.sage with % sagetex.py version 2015/08/26 v3.0-92d9f7a %ef6a4143060336fcf6291bf134f597d4% md5sum of corresponding .sage file (minus "goboom","current_tex_line",and pause/unpause lines)$

Periodic Forcing

A linear second order differential equation is periodically forced if it has the form $\ddot {x} + b\dot {x} + ax = g(t),$ where $g(t)$ is periodic in time; that is, $g(t+T) = g(t)$ for some period $T$ . The simplest kind of forcing is sinusoidal forcing, that is, $g(t)=\sin (\omega t+ t_0)$ where $\frac {\omega }{2\pi }$ is the forcing frequency and $t_0$ is a phase. We simplify the discussion by choosing the phase $t_0$ so that $g(t)=\cos (\omega t)$ and $\omega >0$ .

Suppose, in addition, that the homogeneous equation itself has periodic solutions with internal frequency $\frac {\tau }{2\pi }$ . Such a differential equation is $\ddot {x}+\tau ^2x=0$ ; by rescaling time we can assume that $\tau =1$ . Thus, the homogeneous equation is $\ddot x + x = 0,$ and the forced equation is

$\begin{equation} \label{eq:uspf} \ddot x + x = \cos(\omega t), \end{equation}$ where $\omega >0$ .

We focus on three features of solutions to this equation.

Generally, solutions to (??) are quasiperiodic having two frequencies — just like the torus solutions mentioned in Section ??.
When the forcing frequency is near the internal frequency, the solution has beats.
Resonance occurs when the forcing frequency equals the internal frequency.

The Periodically Forced Undamped Spring

One of the simplest examples of a model differential equation with both a forcing frequency and an internal frequency is the periodically forced undamped spring.

The motion of a forced undamped spring is described by the spring equation given in Chapter ??, (??) with $\mu = 0$ . To simplify the computations, we set the mass to be $m=1$ and suppose that the spring constant is $\kappa =1$ . Then, with periodic forcing $g(t)=\cos (\omega t)$ , we obtain the differential equation (??).

Closed Form Solutions to (??) by Undetermined Coefficients

We can apply the method of undetermined coefficients to solve (??), but there are two cases: $\omega =1$ and $\omega \neq 1$ .

The Case $\omega \not = 1$

We use undetermined coefficients to find a particular solution to the inhomogeneous equation (??). The forcing term $\cos (\omega t)$ is a solution to the differential equation

$\begin{equation} \label{E:omega} \ddot{y} + \omega^2y = 0. \end{equation}$ Thus the annihilator of $\cos (\omega t)$ is $q(D)=D^2+\omega ^2$ . The eigenvalues of the homogeneous equation associated to (??) are $\pm i$ and the eigenvalues of $q(\lambda )$ are $\pm \omega i$ . Thus when $\omega \neq 1$ we can use undetermined coefficients by choosing the general solution to (??) as the trial space for (??). So we set $y(t) = c_1\cos (\omega t) + c_2\sin (\omega t).$ Next, substitute $y$ into (??), obtaining $(1-\omega ^2)(c_1\cos (\omega t) + c_2\sin (\omega t)) = \cos (\omega t).$ This equality holds when $c_1 = \frac {1}{1-\omega ^2} \AND c_2=0.$ Since the general solution of the homogeneous equation associated to (??) is $\alpha \cos (t)+\beta \sin (t),$ the general solution to (??) is $x(t) =\frac {1}{1-\omega ^2}\cos (\omega t) + \alpha \cos (t) + \beta \sin (t),$ when $\omega \neq 1$ .

The Case $\omega = 1$

When $\omega = 1$ the roots of $p(\lambda )$ and $q(\lambda )$ both equal $\pm i$ . Thus, to use undetermined coefficients, we must first find the general solution to $p(D)q(D)x = 0.$ This solution is $x(t) = \alpha _1\cos t + \alpha _2\sin t + c_1t\cos t + c_2t\sin t.$ On setting the solutions to the homogeneous equation associated to (??) to zero (that is, on setting $\alpha _1=\alpha _2=0$ ), we find that the trial space for (??) is: $y(t) = c_1t\cos t + c_2t\sin t.$ Substituting $y(t)$ into (??) yields: $\ddot {y} + y \equiv -2c_1\sin t + 2c_2\cos t = \cos t.$ Therefore, $c_1=0$ and $c_2=\frac {1}{2}$ , and a particular solution of (??) is $x_p(t) = \frac {1}{2}t\sin t.$ The general solution can be written as $x(t) = \frac {1}{2}t\sin t+\alpha \cos t+\beta \sin t.$

To summarize: the general closed form solution to (??) is

$\begin{equation} \label{eq:uspfsoln} x(t) = \alpha\cos t+\beta\sin t + \left\{\begin{array}{lr} \frac{1}{1-\omega ^2}\cos(\omega t) & 0<\omega\neq 1\\ \frac{1}{2}t\sin t & \omega=1 \end{array}\right.\end{equation}$

Types of Solutions to (??)

We use the closed form solution (??) to (??) to identify three different types of solutions: quasiperiodic two-frequency motion, beats, and resonance.

Quasiperiodic Two Frequency Motion

In our discussion we now specify initial conditions. In particular, the solution to (??) with initial conditions $x(0)=1$ and $\dot {x}(0)=0$ is:

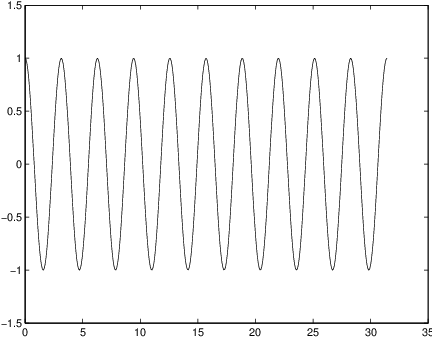
$\begin{equation} \label{e:x(t)reson} x(t) = \cos t + \left\{\begin{array}{ll} \frac{1}{1-\omega ^2}(\cos(\omega t)-\cos t) & \omega \neq 1 \\ \frac{1}{2}t\sin t & \omega=1 \end{array}\right. \end{equation}$ In particular, when $\omega \neq 1$ , the solution (??) is just a linear combination of two periodic functions with different frequencies: $\begin{equation} \label{e:x(t)reson2} x(t) = -\frac{\omega^2}{1-\omega ^2} \cos t + \frac{1}{1-\omega ^2}\cos(\omega t). \end{equation}$ In this way it is straightforward to see that the motion is quasiperiodic with two frequencies.

When $\omega$ is far from $1$ , the solution is very close to the solution to the undamped unforced spring equation. Indeed, note that when the frequency $\omega$ is large, then it follows from (??) that $x(t)$ is approximately equal to $\cos t$ . See Figure ??.

Figure 1: Solutions to: (Left) the unforced undamped spring equation and (Right) the forced spring equation when $\omega =4.5$ .

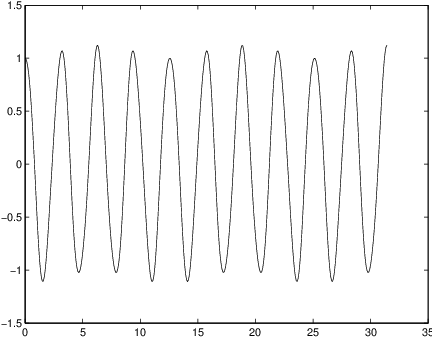
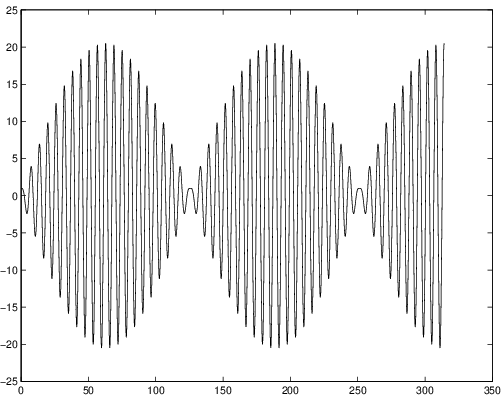
Beats

Using the trigonometric identity $\cos A - \cos B = -2\sin \left (\frac {A+B}{2}\right ) \sin \left (\frac {A-B}{2}\right ),$ we find that the solution $x(t)$ is approximately

$\begin{equation} \label{e:x(t)reson3} x(t) \approx \frac{1}{1-\omega^2} (\cos(\omega t)-\cos(t))= \frac{2}{\omega ^2-1} \sin\left(\frac{\omega+1}{2}t\right)\sin\left(\frac{\omega-1}{2}t\right) \end{equation}$ when $\omega$ is close to $1$ . Note that the first sine term on the right hand side of (??) has period about $2\pi$ while the second sine term has a large period of $4\pi /(\omega -1)$ . For example, when $\omega =1.05$ , this fact leads to periodic behavior of period about $2\pi$ and a modulation of period about $80\pi$ . See Figure ??.

Figure 2: Beats in the solution $x(t)$ to (??) when $\omega =1.05$ and $0\leq t\leq 100\pi$ .

Resonance

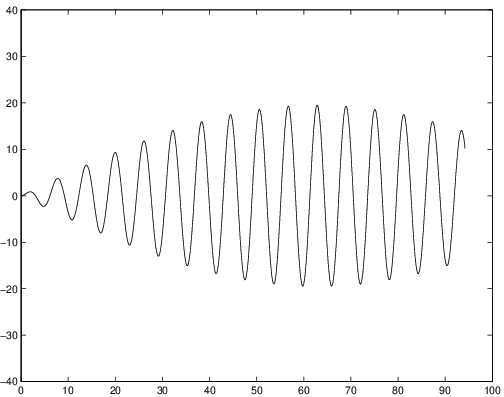
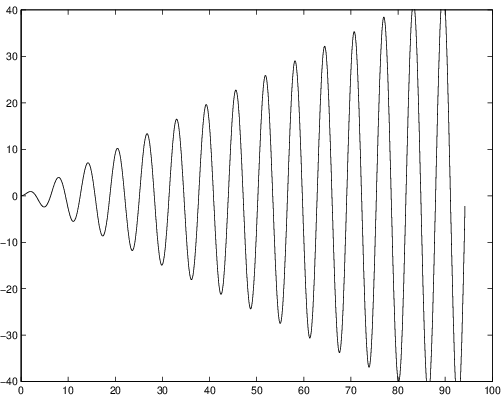
When $\omega = 1$ it follows from (??) that every solution to (??) is unbounded as $t$ goes to infinity. This phenomenon is called resonance, and is due to the fact that the internal frequency is the same as the forcing frequency. The solution to (??) for $\omega =1$ is shown in Figure ?? (right). Resonance shows that when the forcing frequency equals the internal frequency, the forcing amplifies the internal dynamics.

Note that when $\omega$ is close to $1$ the solution follows the solution for $\omega =1$ for some length of time. See Figure ?? where the solutions for $\omega =1.05$ and $\omega =1$ are given. But it is only when $\omega =1$ exactly that unbounded growth or resonance actually occurs while the nearby solution has long term modulation or beats.

Figure 3: Two solutions $x(t)$ from (??) when $\omega =1.05$ and $\omega =1$ for $0\leq t\leq 30\pi$ .

Exercises

Consider the following equation for the periodically forced undamped spring: $\ddot x + \kappa x = A\cos (\omega t).$ (Here the constant of the spring $\kappa$ and the amplitude $A$ of the forcing are assumed to be positive.) Determine the general solution of this equation depending on the constants $\kappa$ , $A$ and $\omega$ . Hint: Proceed as in the text and distinguish between the two different cases where $\omega \not =\sqrt {\kappa }$ and $\omega =\sqrt {\kappa }$ .

The following equation describes the behavior of a damped spring that is forced periodically: $\ddot x + 2\dot x + 2x = \sin (2t).$ Find real constants $\gamma$ and $\delta$ so that $x_p(t) = \gamma \cos (2t)+ \delta \sin (2t),$ is a particular solution of this second order equation. Write down the general solution and discuss the behavior of solutions if time $t$ is going to infinity.

Let $x_\omega (t)$ be the solution to (??) given in (??). Show that $\lim _{\omega \to 1}x_\omega (t) = x_1(t)$ for every real number $t$ .

In Exercises ?? – ?? decide whether or not beats or even resonance occurs in the given differential equations.

$\ddot {x} + 4x = \cos (2t).$

$\ddot {x} + 16x = \sin (3.9 t).$

$\ddot {x} + 9x = \cos (t).$

$\ddot {x} + 9x = \cos (-3t).$

Recall the sinusoidally forced second order equation (??) $\ddot x + x = \cos (\omega t).$ The second order differential operator that annihilates $\cos (\omega t)$ is $q(D)=D^2+\omega ^2$ . It follows that any solution to (??) must satisfy the fourth order equation $\begin{equation} \label{E:ann=res} q(D)(\ddot x + x)=0. \end{equation}$ Compute the characteristic polynomial of (??) and its roots. Since the roots typically form two complex conjugate pairs, observe that there is a connection between the quasiperiodic solutions of this section and those of Section ??. What is the special property of these roots that leads to resonance and why?