Laplace Transforms and Their Computation

$\newenvironment {prompt}{}{} \newcommand {\Sec }[2]{\section {#1}} \newcommand {\trademark }[0]{{R\!\!\!\!\!\bigcirc }} \newcommand {\EXER }[0]{\section *{Exercises}} \newcommand {\CEXER }[0]{} \newcommand {\TEXER }[0]{} \newcommand {\R }[0]{\mbox {$\Bbb {R}$}} \newcommand {\C }[0]{\mbox {$\Bbb {C}$}} \newcommand {\Z }[0]{\mbox {$\Bbb {Z}$}} \newcommand {\N }[0]{\mbox {$\Bbb {N}$}} \newcommand {\D }[0]{\mbox {{\bf D}}} \newcommand {\setmin }[0]{\;\mbox {--}\;} \newcommand {\Matlab }[0]{{M\small {AT\-LAB}} } \newcommand {\Matlabp }[0]{{M\small {AT\-LAB}}} \newcommand {\computer }[0]{\Matlab Instructions} \newcommand {\half }[0]{\mbox {$\frac {1}{2}$}} \newcommand {\compose }[0]{\raisebox {.15ex}{\mbox {{\scriptsize $\circ $}}}} \newcommand {\AND }[0]{\quad \mbox {and}\quad } \newcommand {\vect }[2]{\left (\begin {array}{c} #1_1 \\ \vdots \\ #1_{#2}\end {array}\right )} \newcommand {\mattwo }[4]{\left (\begin {array}{rr} #1 & #2\\ #3 &#4\end {array}\right )} \newcommand {\mattwoc }[4]{\left (\begin {array}{cc} #1 & #2\\ #3 &#4\end {array}\right )} \newcommand {\vectwo }[2]{\left (\begin {array}{r} #1 \\ #2\end {array}\right )} \newcommand {\vectwoc }[2]{\left (\begin {array}{c} #1 \\ #2\end {array}\right )} \newcommand {\inv }[0]{^{-1}} \newcommand {\CC }[0]{{\cal C}} \newcommand {\CCone }[0]{\CC ^1} \newcommand {\Span }[0]{{\rm span}} \newcommand {\rank }[0]{{\rm rank}} \newcommand {\trace }[0]{{\rm tr}} \newcommand {\RE }[0]{{\rm Re}} \newcommand {\IM }[0]{{\rm Im}} \newcommand {\nulls }[0]{{\rm null\;space}} \newcommand {\dps }[0]{\displaystyle } \newcommand {\arraystart }[0]{\renewcommand {\arraystretch }{1.8}} \newcommand {\arrayfinish }[0]{\renewcommand {\arraystretch }{1.2}} \newcommand {\Start }[1]{\vspace {0.08in}\noindent {\bf Section~\ref {#1}}} \newcommand {\exer }[1]{\noindent {\bf \ref {#1}}} \newcommand {\ans }[0]{} \newcommand {\matthree }[9]{\left (\begin {array}{rrr} #1 & #2 & #3 \\ #4 & #5 & #6 \\ #7 & #8 & #9\end {array}\right )} \newcommand {\cvectwo }[2]{\left (\begin {array}{c} #1 \\ #2\end {array}\right )} \newcommand {\cmatthree }[9]{\left (\begin {array}{ccc} #1 & #2 & #3 \\ #4 & #5 & #6 \\ #7 & #8 & #9\end {array}\right )} \newcommand {\vecthree }[3]{\left (\begin {array}{r} #1 \\ #2 \\ #3\end {array}\right )} \newcommand {\cvecthree }[3]{\left (\begin {array}{c} #1 \\ #2 \\ #3\end {array}\right )} \newcommand {\cmattwo }[4]{\left (\begin {array}{cc} #1 & #2\\ #3 &#4\end {array}\right )} \newcommand {\thehelp }[0]{\thesection .\arabic {equation}} \newcommand {\matlabEquation }[0]{\let \oldtheequation \theequation \renewcommand {\theequation }{\oldtheequation *}\begin {equation}} \newcommand {\HyperFirstAtBeginDocument }[0]{\AtBeginDocument } \newcommand {\epstopdfsetup }[0]{\setkeys {ETE}} changed the theorem header of amsthm failed\MessageBreak }}} \newcommand {\GetTitleStringSetup }[0]{\setkeys {gettitlestring}} \newcommand {\Sectionformat }[2]{#1}$ $% This file was *autogenerated* from laplaceTransformsAndTheirComputation.sagetex.sage with % sagetex.py version 2015/08/26 v3.0-92d9f7a %287ca12c17072934e62a2c76df6e930f% md5sum of corresponding .sage file (minus "goboom","current_tex_line",and pause/unpause lines)$

This section divides into three parts. In the first part, we give an explicit formula for the Laplace transform and verify that this formula satisfies properties (??). In the second part, we compute a table of Laplace transforms for a number of special functions including step functions and impulse functions. In the third part we discuss two properties of Laplace transforms that are useful when computing inverse Laplace transforms of functions of the type that appear when solving forced second order equations.

Let $x(t)$ be a function that is defined for $0\le t < \infty$ . Then the function ${\cal L}[x](s)$ is defined by $\begin{equation} \label{E:laplace} {\cal L}[x](s) = \int_0^{\infty} e^{-st} x(t)\; dt \end{equation}$ and is called the Laplace transform of $x(t)$ .

Note that the Laplace transform is an improper integral — which implies that some care must be taken when discussing its properties. Indeed, for some functions the Laplace transform does not exist for all values of $s$ . What usually happens is that the Laplace transform exists for all values of $s$ larger than some number $a$ . As an example, we compute (??) directly using Definition ??. Let $x(t)=e^{at}$ and compute

$\begin{equation} \label{e:expat} {\cal L}[x](s) = \int_0^{\infty} e^{(a-s)t}\; dt= \lim\limits_{h\to \infty} \frac{1}{s-a}\left( 1-e^{(a-s)h} \right) =\left\{ \begin{array}{cl} \frac{\dps 1}{\dps s-a} & \mbox{for $s>a$,}\\ \infty & \mbox{for $s\le a$.}\end{array}\right. \end{equation}$

The Laplace Transform is Linear

The first step in verifying properties (??) is to show that the Laplace transform $\cal L$ is linear, that is, to show that (??)(a) holds.

Suppose $x(t)$ and $y(t)$ are functions for which the Laplace transforms ${\cal L}[x](s)$ , ${\cal L}[y](s)$ exist for $s>a$ , and let $c$ be real. Then for all $s>a$ $\begin{equation} \label{eq:linLap} \begin{array}{rcl} {\cal L}[x + y] & = & {\cal L}[x] + {\cal L}[y] \\ {\cal L}[cx] & = & c{\cal L}[x]. \end{array} \end{equation}$

Proof: Using properties of integrals we obtain for each $s>a$
$\begin{eqnarray*} {\cal L}[x+y](s) &=& \int_0^{\infty} e^{-st} (x(t)+y(t))\; dt\\ &=& \int_0^{\infty} e^{-st} x(t)\; dt + \int_0^{\infty} e^{-st} y(t)\; dt\\ &=& {\cal L}[x](s)+ {\cal L}[y](s). \end{eqnarray*}$
A similar computation verifies that $\cal L$ commutes with scalar multiplication. $\blacksquare$

The Derivative Property of Laplace Transforms is Valid

Next we verify the important derivative property (??)(c) of the Laplace transform.

Suppose that $x$ is a differentiable function such that $|x(t)|\le Me^{at}$ for constants $a>0$ and $M>0$ . Then

the Laplace transform ${\cal L}[x](s)$ exists for $s>a$ ;
${\cal L}[\dot x](s) = s{\cal L}[x](s) - x(0) \quad \mbox {for $s>a$.}$

Proof: (a) Observe that by the assumption on the growth of $x(t)$ we have for $s>a$ $\lim \limits _{h\to \infty }\left |\int _0^h e^{-st} x(t)\; dt\right | \le \lim \limits _{h\to \infty }\int _0^h Me^{(a-s)t}\; dt =\lim \limits _{h\to \infty }\left .\frac {Me^{(a-s)t}}{a-s}\right |_0^h =\frac {M}{s-a}<\infty .$ Hence the Laplace transform ${\cal L}[x](s)$ exists for $s>a$ .
(b) First note that $\lim \limits _{h\to \infty } |e^{-sh} x(h)|\le \lim \limits _{h\to \infty } |Me^{(a-s)h}| = 0.$ Now use the definition of improper integrals and integration by parts to compute
$\begin{eqnarray*} {\cal L}[\dot x](s) &=& \int_0^{\infty} e^{-st} \dot x(t)\; dt\\ & = & \lim\limits_{h\to \infty}\int_0^h e^{-st} \dot x(t)\; dt\\ & = & \lim\limits_{h\to \infty}\left(\left.e^{-st}x(t)\right|_0^h - \int_0^h (-s)e^{-st} x(t)\; dt\right)\\ &=& \lim\limits_{h\to \infty} \left( e^{-sh} x(h) - x(0)\right) + s\lim\limits_{h\to \infty} \int_0^h e^{-st} x(t)\; dt\\ &=& -x(0) + s{\cal L}[x](s) \end{eqnarray*}$
for $s>a$ . $\blacksquare$

Finally, we remark that (??)(b) is valid, but that its proof is beyond the scope of this course. One method of proof is to develop an explicit integral formula for the inverse Laplace transform.

A Table of Laplace Transforms

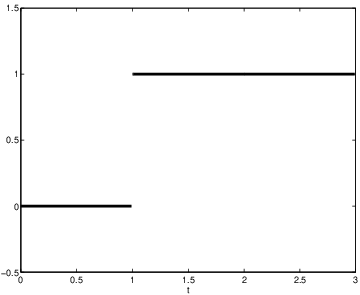
In order to solve differential equations using the method of Laplace transforms, we need to have a table of Laplace transforms readily available. We now compute the Laplace transform for the functions in Table ??. These functions include the discontinuous step function $H_c(t) = \left \{\begin {array}{ll} 0 & \mbox {for $0\le t < c$}\\ 1 & \mbox {for $t\ge c$} \end {array}\right .$ where $c$ is a positive constant and the hitherto undefined Dirac delta function $\delta _c(t)$ . See Figure ?? for a graph of $H_1$ .

Figure 1: Graph of $H_1(t)$ .

We derive some of these formulas by using the Laplace transform formulas for derivatives (??)(c) and (??). (We could compute these transforms directly by integration from Definition ??, but the method we choose is simpler and illustrates the power of the derivative formulas.) Note that we have already computed the Laplace transforms of the first two functions in Table ?? when deriving (??).


Function $y(t)$	Laplace transform ${\cal L}[y](s)$

$1$	$\frac {\dps 1}{\dps s}$
$e^{at}$	$\frac {\dps 1}{\dps s-a}$
$\cos (\tau t)$	$\frac {\dps s}{\dps s^2 + \tau ^2}$
$\sin (\tau t)$	$\frac {\dps \tau }{\dps s^2 + \tau ^2}$
$t^n$	$\frac {\dps n!}{\dps s^{n+1}}$
$H_c(t)$	$\frac {1}{\dps s}e^{-cs}$
$\delta _c(t)$	$e^{-cs}$

Table 1: Laplace transforms.

The Laplace Transforms: ${\cal L}[\cos (\tau t)]$ and ${\cal L}[\sin (\tau t)]$

To compute ${\cal L}[x]$ where $x(t)=\cos (\tau t)$ , observe that $x(t)$ is a solution to the initial value problem

$\begin{eqnarray*} \ddot{x}+\tau^2 x & = & 0\\ x(0) & = & 1 \\ \dot{x}(0) & = & 0. \end{eqnarray*}$

It follows from (??) that $s^2{\cal L}[x] - s + \tau ^2 {\cal L}[x] = 0.$ Hence ${\cal L}[x] = \frac {s}{s^2+\tau ^2},$ as desired. Similarly, note that $x(t)=\sin (\tau t)$ satisfies the initial value problem

$\begin{eqnarray*} \ddot{x}+\tau^2 x & = & 0 \\ x(0) & = & 0 \\ \dot{x}(0) & = & \tau. \end{eqnarray*}$

The computation of the Laplace transform for $\sin (\tau t)$ proceeds identically as the computation of ${\cal L}[\cos (\tau t)]$ .

The Laplace Transform: ${\cal L}[t^n]$

Next, we compute ${\cal L}[t^n]$ by applying (??)(c) $n$ times. That is, ${\cal L}[t^n] = \frac {n}{s}{\cal L}[t^{n-1}] = \cdots = \frac {n!}{s^n}{\cal L}[1] = \frac {n!}{s^{n+1}}.$

The Laplace Transform: ${\cal L}[H_c(t)]$

We compute the Laplace transform of the step function $H_c(t)$ by direct integration. ${\cal L}[H_c](s) = \int _0^{\infty } e^{-st}H_c(t)\; dt = \int _c^{\infty } e^{-st}\; dt =\left \{ \begin {array}{cl} \frac {1}{\dps s}e^{-cs} & \mbox {for $s>0$,}\\ \infty & \mbox {for $s\le 0$.}\end {array}\right .$

The Laplace Transform of Dirac Delta Functions

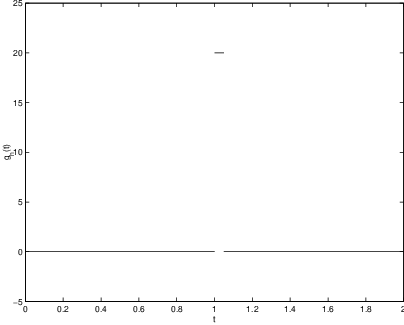
Suppose that a strong external force is applied at time $t=c$ , but only for a very short time $h$ . Then the forcing function is approximated by

$\begin{equation} \label{eq:deltah} \begin{array}{rcl} g_h(t) & = & \left\{\begin{array}{cc} \frac{1}{h} & c\leq t \leq c+h \\ 0 & \mbox{otherwise} \end{array} \right. \\ & = & \frac{1}{h} \left(H_c(t)-H_{c+h}(t)\right). \end{array} \end{equation}$ The graph of $g_h$ is given in Figure ??. It is not clear how to take the limit of $g_h(t)$ as $h\to 0$ in (??), since this limit leads to a ‘function’ that is infinity at $c$ and zero elsewhere. Despite this difficulty, the limit is called the Dirac delta function and is denoted by $\delta _c(t)$ . We compute the Laplace transform of the $\delta _c(t)$ by first computing the Laplace transform of the approximating function $g_h(t)$ and then taking the limit of the Laplace transforms of the approximation as $h\to 0$ .

Figure 2: Graph of the approximating function $g_h(t)$ of (??) for $c=1$ and $h=0.05$ .

The Laplace transform of the approximating function $g_h(t)$ is found using the linearity of $\cal L$ and Table ??, that is, ${\cal L}[g_h] = \frac {1}{h} \left ({\cal L}[H_c]-{\cal L}[H_{c+h}]\right ) = \frac {1}{h}\left (\frac {1}{s}e^{-cs}- \frac {1}{s}e^{-(c+h)s}\right ) = \frac {1}{s}e^{-cs}\frac {1-e^{-sh}}{h}.$ We claim that $\lim _{h\to 0} \left (\frac {1-e^{-sh}}{h}\right )=s,$ from which it follows that $\lim _{h\to 0} {\cal L}[g_h](s)=e^{-cs}.$ This result justifies writing

$\begin{equation} \label{e:lapdel} {\cal L}[\delta_c] = e^{-cs}. \end{equation}$ To verify the claim, let $f(y)=e^{-sy}$ and recall that $f'(0) = \lim _{h\to 0} \frac {f(h)-f(0)}{h} =\lim _{h\to 0} \frac {e^{-sh}-1}{h}.$ Since $f'(0)=-s$ , it follows that $\lim _{h\to 0} \left (\frac {1-e^{-sh}}{h}\right )=-f'(0)=s,$ as claimed.

Additional Techniques for Laplace Transforms

At the end of Section ?? we showed that when solving second order differential equations by the method of Laplace transforms, it is necessary to compute inverse Laplace transforms of functions like

$\begin{equation} \label{E:1sttype} \frac{1}{(s-B)^2+C^2} \AND \frac{s-B}{(s-B)^2+C^2} \end{equation}$ and $\begin{equation} \label{2ndtype} \frac{1}{(s-B)^2+C^2}G(s) \AND \frac{s-B}{(s-B)^2+C^2}G(s) \end{equation}$ where $G(s)$ is the Laplace transform of the forcing function $g(t)$ . See (??).

Inverse Laplace Transforms of Shifted Functions

The next proposition enables us to calculate inverse Laplace transforms for functions of type (??).

Suppose that $Y(s)={\cal L}[y(t)](s)$ exists. Then $\begin {array}{rrcl} \mbox {(a)} & {\cal L}[e^{at}y(t)](s) & = & Y(s-a)\\ \mbox {(b)} & {\cal L}^{-1}[Y(s-a)](t) & = & e^{at}y(t). \end {array}$

Proof: To verify (a) compute ${\cal L}[e^{at}y(t)](s) = \int _0^{\infty } e^{-st}e^{at} y(t)\; dt = \int _0^{\infty } e^{-(s-a)t} y(t)\; dt = {\cal L}[y(t)](s-a) = Y(s-a).$ Part (b) follows by applying the inverse Laplace transform to both sides of (a). $\blacksquare$

For example, suppose that we want to compute the inverse Laplace transform of

$\begin{equation} \label{e:exlappf} \frac{s-1}{s^2+2s+5}. \end{equation}$ The first step in this computation is to write the denominator as the sum of two squares and to shift the numerator. That is, $\begin{equation} \label{e:pf1} \frac{s-1}{s^2+2s+5} = \frac{(s+1)-2}{(s+1)^2+4} = \frac{s+1}{(s+1)^2+4} - 2\frac{1}{(s+1)^2+4}. \end{equation}$ We can now find the inverse Laplace transform of the right hand side of (??). Except for the shift of $s$ to $s+1$ , the rearranged expression (??) is one whose inverse Laplace transform can be read from Table ??. More precisely, let $Y(s) = \frac {s}{s^2+4} - 2\frac {1}{s^2+4},$ so that the right hand side of (??) is $Y(s+1)$ . Using Table ?? the inverse Laplace transform of $Y(s)$ is $\begin{equation} \label{e:exlappf2} {\cal L}\inv[Y(s)](t) = {\cal L}\inv\left[\frac{s}{s^2+4} - 2\frac{1}{s^2+4}\right](t) = \cos(2t) - \sin(2t) = y(t). \end{equation}$ Using Proposition ??(b) we can compute the inverse Laplace transform of $Y(s+1)$ as ${\cal L}^{-1}[Y(s+1)](t) = e^{-t}y(t)$ That is, ${\cal L}^{-1}\left [\frac {s-1}{s^2+2s+5}\right ](t) = e^{-t}(\cos (2t)-\sin (2t)).$

Another Useful Property of the Laplace Transform

Next, we examine the Laplace transform of a function that is multiplied by the jump function $H_c(t)$ and by doing so we will be able to compute the inverse Laplace transform of functions like (??) when $G(s)$ is the Laplace transform of a discontinuous forcing function.

Suppose that $Y(s)={\cal L}[y(t)](s)$ exists. Then $\begin {array}{rrcl} \mbox {(a)} & {\cal L}[H_c(t)y(t-c)](s) & = & e^{-cs} Y(s) \\ \mbox {(b)} & {\cal L}^{-1}[e^{-cs}Y(s)](t) & = & H_c(t)y(t-c). \end {array}$

Proof: (a) Compute ${\cal L}[H_c(t)y(t-c)](s) = \int _0^{\infty } e^{-st}H_c(t) y(t-c)\; dt = \int _c^{\infty } e^{-st}y(t-c)\; dt.$ On substituting $t+c$ for $t$ we obtain ${\cal L}[H_c(t)y(t-c)](s)=\int _0^{\infty } e^{-s(t+c)}y(t)\; dt =e^{-cs} \int _0^{\infty } e^{-st}y(t)\; dt =e^{-cs} Y(s).$ Part (b) follows by applying the inverse Laplace transform to both sides of (a). $\blacksquare$

As an application of Proposition ??(b), we find that ${\cal L}^{-1}\left [ e^{-s}\frac {s}{s^2+4}\right ](t)= H_1(t){\cal L}^{-1}\left [ \frac {s}{s^2+4}\right ](t-1)= H_1(t)\cos (2(t-1)).$

Exercises

In Exercises ?? – ?? compute the Laplace transform for each function $x(t)$ :

$x(t) = 4\cos (t-1)$ ,

$x(t) = \sin (3(t-2))$ ,

$x(t) = (t-3)^2$ .

$x(t) = te^{-2t}$ .

In Exercises ?? – ??, use Laplace transforms to compute the solution to the given initial value problem.

$\ddot {x} + 2\dot x +5x = 0, \quad x(0) = 2, \quad \dot {x}(0) = -6$ .

$\ddot x +4\dot x +20 x=0,\quad x(0)=1,\quad \dot {x}(0)=-6$ .

$\ddot x -6\dot x +13 x=1,\quad x(0)=0,\quad \dot {x}(0)=1$ .

$\ddot {x} + 2\dot {x} - 3x = 1, \quad x(0) = 2, \quad \dot {x}(0) = 0$ .

$\ddot {x} + 2\dot {x} - 8x = e^t, \quad x(0) = 1, \quad \dot {x}(0) = 2$ .

Suppose that $z(t)=ty(t)$ . Using (??) show that ${\cal L}[z](s) = -\frac {\dps d}{\dps ds} {\cal L}[y](s).$