Geometry of Differentiability

$\newenvironment {prompt}{}{} \newcommand {\DeclareMathOperator }[2]{\@OldDeclareMathOperator {##1}{##2}\immediate \write \myfile {\unexpanded {\DeclareMathOperator }{\unexpanded {##1}}{\unexpanded {##2}}}} \newcommand {\ungraded }[0]{} \newcommand {\reserved@a }[2]{} \newcommand {\HyperFirstAtBeginDocument }[0]{\AtBeginDocument } \newcommand {\reserved@a }[1]{} \newcommand {\reserved@a }[2]{} \newcommand {\vnameref }[1]{\unskip ~\nameref {##1}\@vpageref [\unskip ]{##1}} \newcommand {\ref }[0]{\@ifstar \@refstar \T@ref } \newcommand {\pageref }[0]{\@ifstar \@pagerefstar \T@pageref } \newcommand {\nameref }[0]{\@ifstar \@namerefstar \T@nameref } \newcommand {\reserved@a }[2]{} \newcommand {\reserved@a }[0]{\AtBeginDocument } \newcommand {\reserved@a }[1]{} \newcommand {\reserved@a }[2]{}$

In single variable calculus, derivatives were closely related to the slope of the tangent line to a graph at a point. We used this idea of the slope of the tangent line to define derivatives as a limit of slopes of secant lines, $f'(a) = \lim _{h\rightarrow 0}\frac {f(a+h)-f(a)}{h}.$

In the other direction, we were able to use differentiation rules to more easily find the equation for the tangent line to a graph at a point.

We’ll find the equation for the tangent line to the graph of $f(x)=x^3+2x+1$ at $x=2$ .

We can find the slope of the tangent line by computing $f'(2)$ . Using differentiation rules, we have $f'(x) = \answer {3x^2+2}.$ Plugging in $x=2$ , we have $f'(2) = \answer {14}$ .

Since the tangent line will have to pass through the point $(2,f(2))$ , we compute $f(2) = \answer {13}.$

So, the tangent line will pass through the point $(2,13)$ , and will have slope $14$ . Writing the equation of the line in point-slope form, we have $y-13 = \answer {14(x-2)}.$

When a single variable function is differentiable, we can use the above method to find an equation for the tangent line. In addition, the tangent line provides us with a good linear approximation for the function.

We would like to do something analogous for multivariable functions, but this raises a few questions. What would be the equivalent of the tangent line? What does it mean for a function to be differentiable?

As we begin to explore these questions, we’ll focus on functions $\mathbb {R}^2\rightarrow \mathbb {R}$ , so that we can visualize their graphs.

Geometric Interpretation of Differentiability

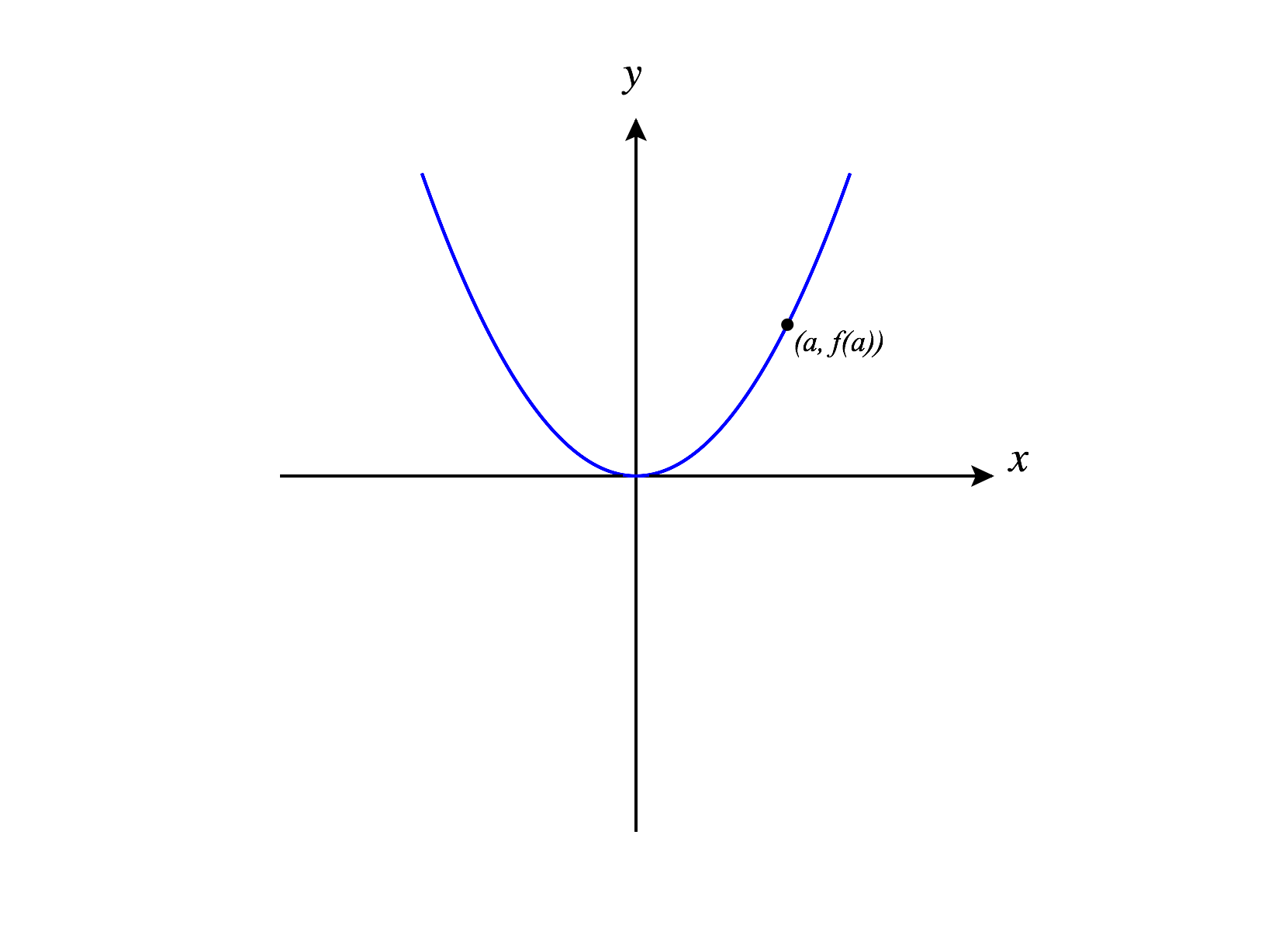
In single variable calculus, we could get a good sense of whether a function was differentiable by looking at its graph.

For each of the graphs, determine whether the given function is differentiable at $x=a$ .

differentiable not differentiable

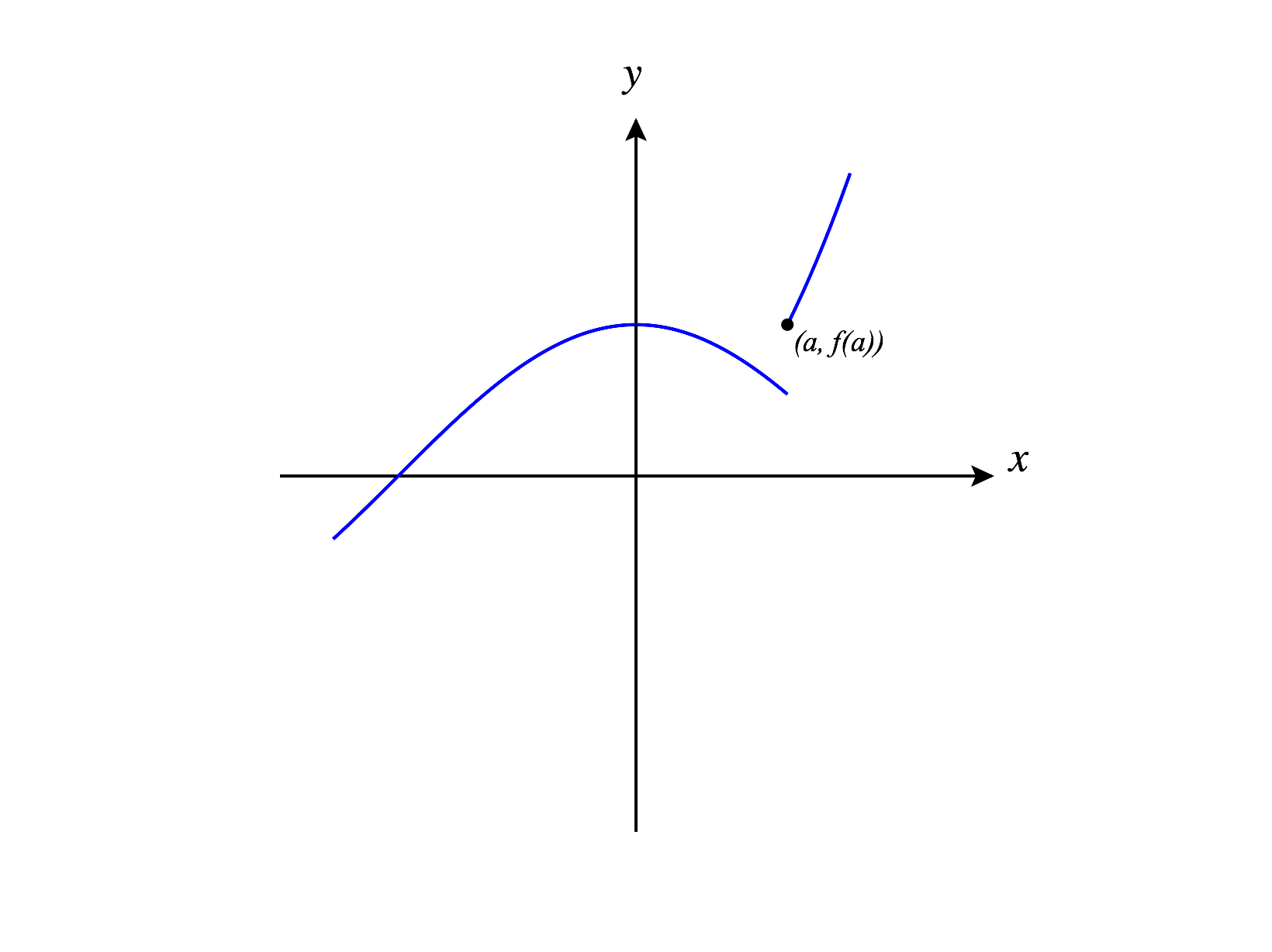
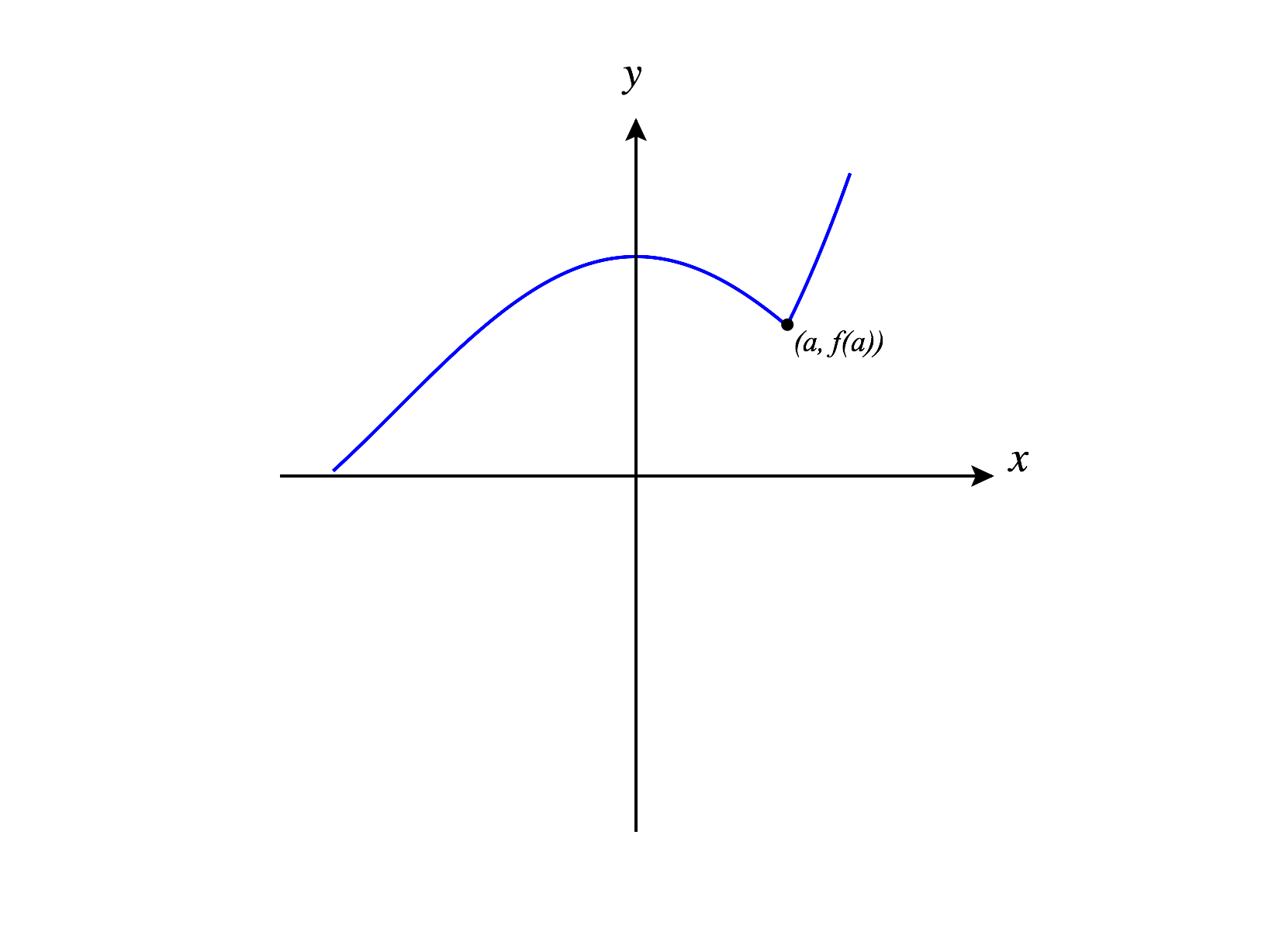
If there is a discontinuity or some sort of corner or cusp in the graph at a point, then the function will not be differentiable at that point. Roughly speaking, if we “zoom in” on the graph of a function near a point, and the graph looks very close to a line, then the function will be differentiable at that point.

We’ll extend this idea to make our first, informal definition of differentiability for a function from $\mathbb {R}^2$ to $\mathbb {R}$ .

(Informal Definition) Consider a function $f:\mathbb {R}^2\rightarrow \mathbb {R}$ . Suppose for some point $(a,b)$ in $\mathbb {R}^2$ , if we zoom in on the graph of $f$ near the point $(a,b)$ , the graph of $f$ looks like a plane. Then $f$ is differentiable at $(a,b)$ .

Although this definition provides us with nice geometric intuition for determining if a function is differentiable, it’s not at all precise or rigorous. Eventually, we’ll need a more formal definition of differentiability, so we’ll return to this concept later.

For now, let’s use this informal definition to investigate differentiability for a couple of functions.

Consider the function $f(x,y) = xy+2x+y$ , graphed below.

Is $f$ differentiable at $(0,0)$ ?

Yes. No.

Consider the function $f(x,y) = \begin {cases} 1-|y| & \text {if }|y|\leq |x| \\ 1-|x| & \text {if }|y| > |x| \end {cases},$ graphed below.

Is f differentiable at $(0,0)$ ?

Yes. No.

The tangent plane

If a function $f:\mathbb {R}^2\rightarrow \mathbb {R}$ is differentiable, when we zoom in, the graph will look like a plane. Because of this, there will be a plane that’s a good linear approximation for the function near that point. We can use the partial derivatives with respect to $x$ and $y$ to find an equation for this plane, which we call the tangent plane.

If $f:\mathbb {R}^2\rightarrow \mathbb {R}$ is differentiable at $(a,b)$ , then the tangent plane to the graph of $f$ at $(a,b)$ is defined by the equation $z=f(a,b)+f_x(a,b)(x-a)+f_y(a,b)(y-b).$

Let’s revisit our previous examples, and see what happens with the tangent plane.

Consider the function $f(x,y) = xy+2x+y$ , which we found is differentiable at the point $(0,0)$ . Let’s find an equation for the tangent plane to the graph of $f$ at $(0,0)$ .

We begin by finding the partial derivatives with respect to $x$ and $y$ .

$\begin{align*} f_x(x,y) &= \answer{y+2}\\ f_y(x,y) &= \answer{x+1} \end{align*}$

At $(0,0)$ , we have

$\begin{align*} f_x(0,0) &= \answer{2},\\ f_y(0,0) &= \answer{1}. \end{align*}$

Finding the value of $f$ at $(0,0)$ , we have $f(0,0) = \answer {0}.$ Putting all of this together, we obtain an equation for the tangent plane to the graph of $f$ at $(0,0)$ .

$\begin{align*} z &=f(a,b)+f_x(a,b)(x-a)+f_y(a,b)(y-b)\\ &= \answer{2x+y} \end{align*}$

Consider the function $f(x,y) = \begin {cases} 1-|y| & \text {if }|y|\leq |x| \\ 1-|x| & \text {if }|y| > |x| \end {cases},$ which we found is not differentiable $(0,0)$ . Even though this function is not differentiable, let’s see what happens when we try to find an equation for the tangent plane.

To compute the partial derivatives with respect to $x$ and $y$ , we’ll need to use the limit definition.

$\begin{align*} f_x(0,0) &= \lim_{h\rightarrow 0}\frac{f(0+h,0)-f(0,0)}{h}\\ &= \lim_{h\rightarrow 0}\frac{(1-|0|)-(1-|0|)}{h}\\ &= \lim_{h\rightarrow 0}\frac{0}{h}\\ &= 0\\ f_y(0,0) &= \lim_{h\rightarrow 0}\frac{f(0,0+h)-f(0,0)}{h}\\ &= \lim_{h\rightarrow 0}\frac{(1-|0|)-(1-|0|)}{h}\\ &= \lim_{h\rightarrow 0}\frac{0}{h}\\ &= 0 \end{align*}$

We can also find $f(0,0)$ , $f(0,0)= 1.$

So, we have all of the necessary pieces to find an equation for the (nonexistent) “tangent plane”:

$\begin{align*} z &=f(a,b)+f_x(a,b)(x-a)+f_y(a,b)(y-b)\\ &= 1. \end{align*}$

However, we decided that the function wasn’t differentiable at $(0,0)$ , so the graph does not have a tangent plane at the point.

This example brings up a couple of important points.

It’s possible for the partial derivatives of a function to all exist, and yet the function is not differentiable.
It’s possible that we can find the equation $z =f(a,b)+f_x(a,b)(x-a)+f_y(a,b)(y-b)$ , and yet $f$ has no tangent plane at the point $(a,b)$ .

For these reasons, differentiability is a much more subtle concept in multivariable calculus than it was in single variable calculus, and our next task will be to find a formal definition for differentiability.