We’ve seen how points in can be written using polar coordinates, and we’ve seen how polar coordinates can be useful for describing some shapes that are difficult to describe in Cartesian coordinates.
We’d now like to extend this idea to , using a coordinate system called cylindrical coordinates. Like polar coordinates, cylindrical coordinates will be useful for describing shapes in that are difficult to describe using Cartesian coordinates. Later in the course, we will also see how cylindrical coordinates can be useful in calculus, when evaluating limits or integrating in Cartesian coordinates is very difficult.
Cylindrical coordinates
Cylindrical coordinates are really just an extension of polar coordinates. For points in the -plane, we describe them using and , where is the distance from the origin and is the angle with the positive -axis. We then append a -coordinate, which tells us the vertical displacement of the point.
In other words, for a point given in Cartesian coordinates, we consider its projection onto the -plane, which gives us the point in . We find the polar coordinates of the point , and then we write our original point in cylindrical coordinates as .
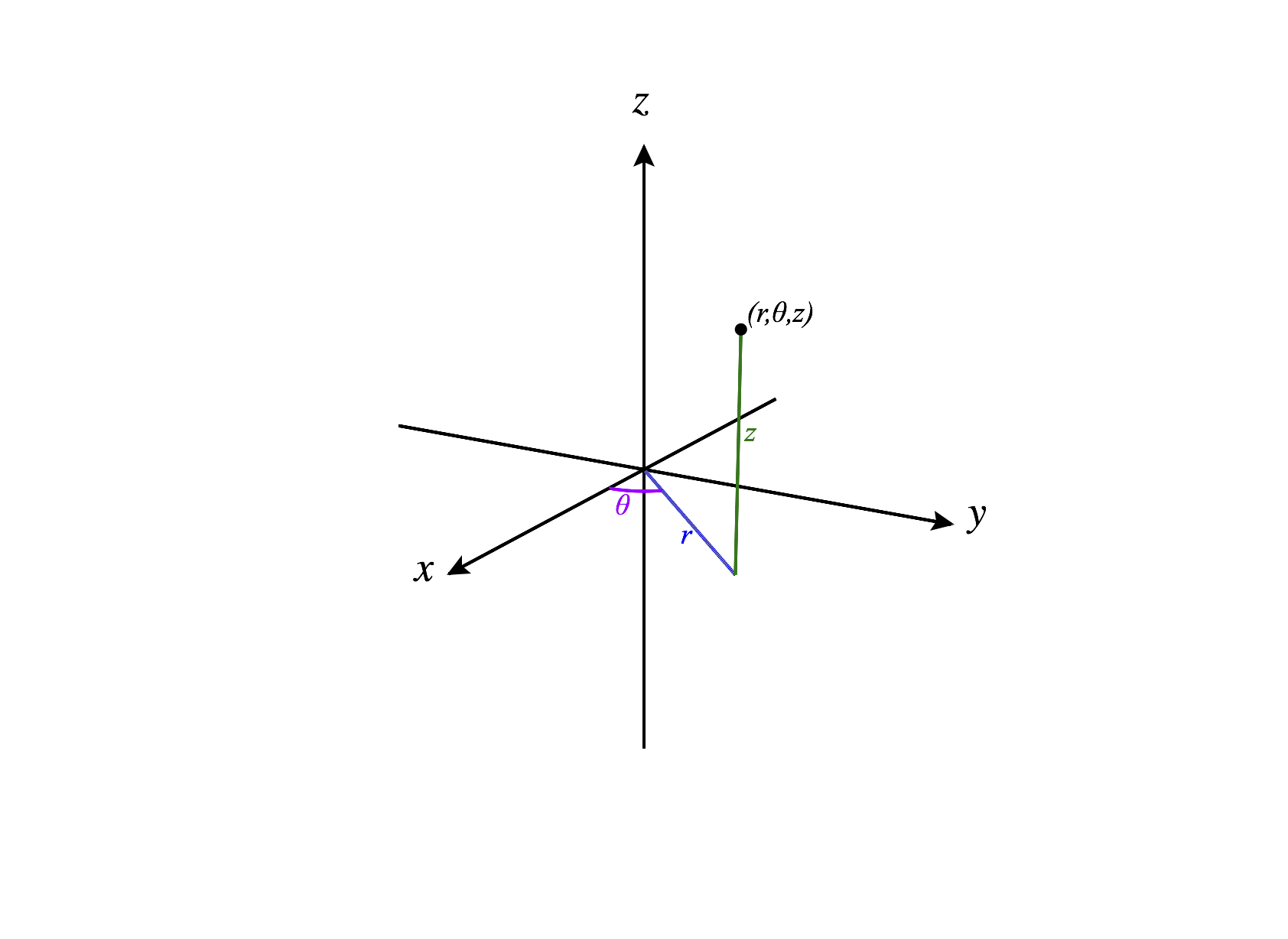
We can figure out and by projecting our point onto the -plane, giving us the point in . Then we represent in polar coordinates, so we have For last coordinate, , notice that this is telling us the height of the point, which is the exact same as the -coordinate of the point written in Cartesian coordinates! So, our coordinate is , and the point can be written in cylinderical coordinates as
You may use this applet to experiment with how changing the different coordinates changes the point given in cylindrical coordinates.
Uniqueness
When we studied polar coordinates, we saw that there were many different ways to represent a point. For example, the point could be written as , , or even . And the origin was especially devious, it could be written as for any angle .
Because of this and the relationship between polar and cylindrical coordinates, it’s not surprisingly that cylindrical coordinates have similar issues with uniqueness. For example, the point can be written as , , , and so on. Any point on the -axis can be written as , where is its -coordinate, and is any angle.
As with polar coordinates, in situations where uniqueness is important, we will often make the restrictions and . Unfortunately, this restriction does not completely eliminate the issues with uniqueness, as there are still infinitely ways to describe the origin.
Constant-coordinate surfaces
Let’s look at what happens in cylindrical coordinates when we set each of the coordinates to be constant, with the standard restrictions that and . This can give us insight to how cylindrical coordinates behave.
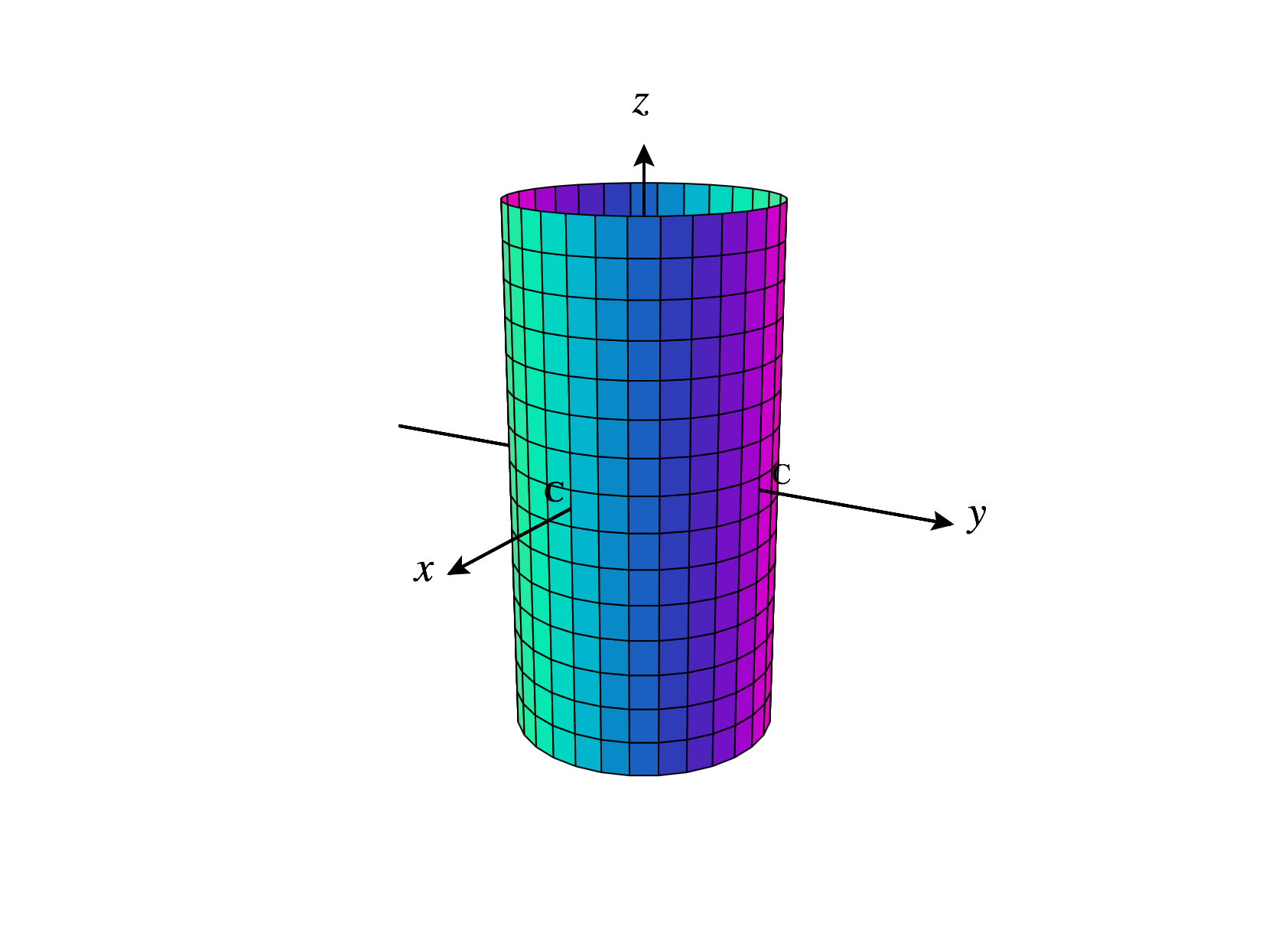
We’ll begin by examining the set of points , where is a constant. We have that is constant, which means that the distance between any such point and the axis is constant, . Also, and can be anything. This will give us the cylinder of radius , centered at the -axis.
Next, we’ll investigate the set of points , where is constant. Let’s consider the projection of this point onto the -plane. The projection will make an angle with the positive -axis, and have distance from the origin. The height of the point can be any real number. From these observations, we conclude that the set of such points is the following half plane in .

Note that if we didn’t have the restriction , we would get an entire plane rather than a half plane.
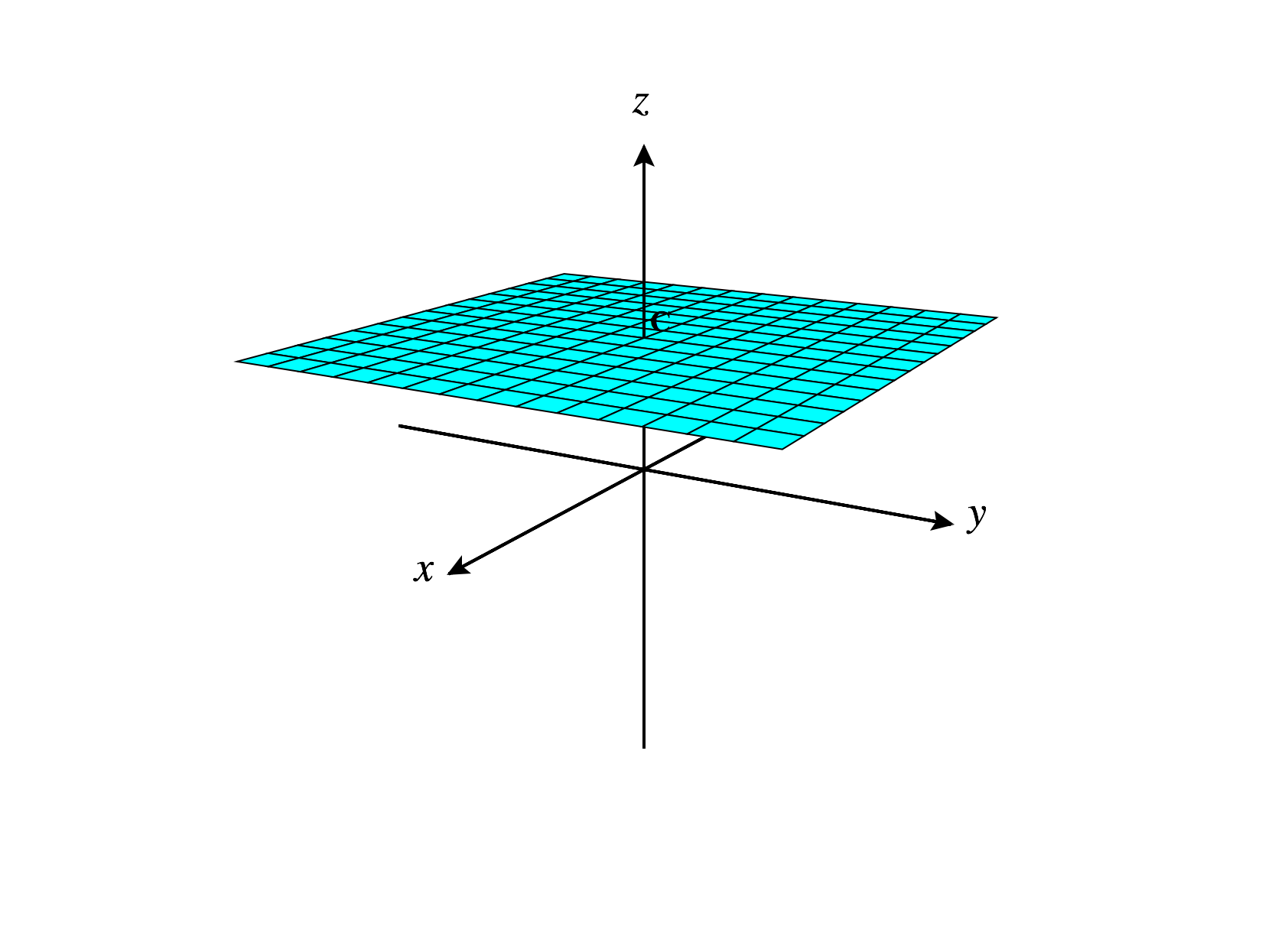
Finally, we’ll consider the set of points , where is constant. Since , we will only have points at height . Varying and will then give us all points in the plane at height parallel to the -plane, as below.
Converting between Cartesian and cylindrical coordinates
Perhaps not surprisingly, converting between Cartesian coordinates and cylindrical coordinates is very similar to how we converted between Cartesian coordinates and polar coordinates. That is, we can use the equations:
Using , we have You may recognize this as the top half of the sphere of radius centered at the origin. You could also rewrite this as keeping in mind that .
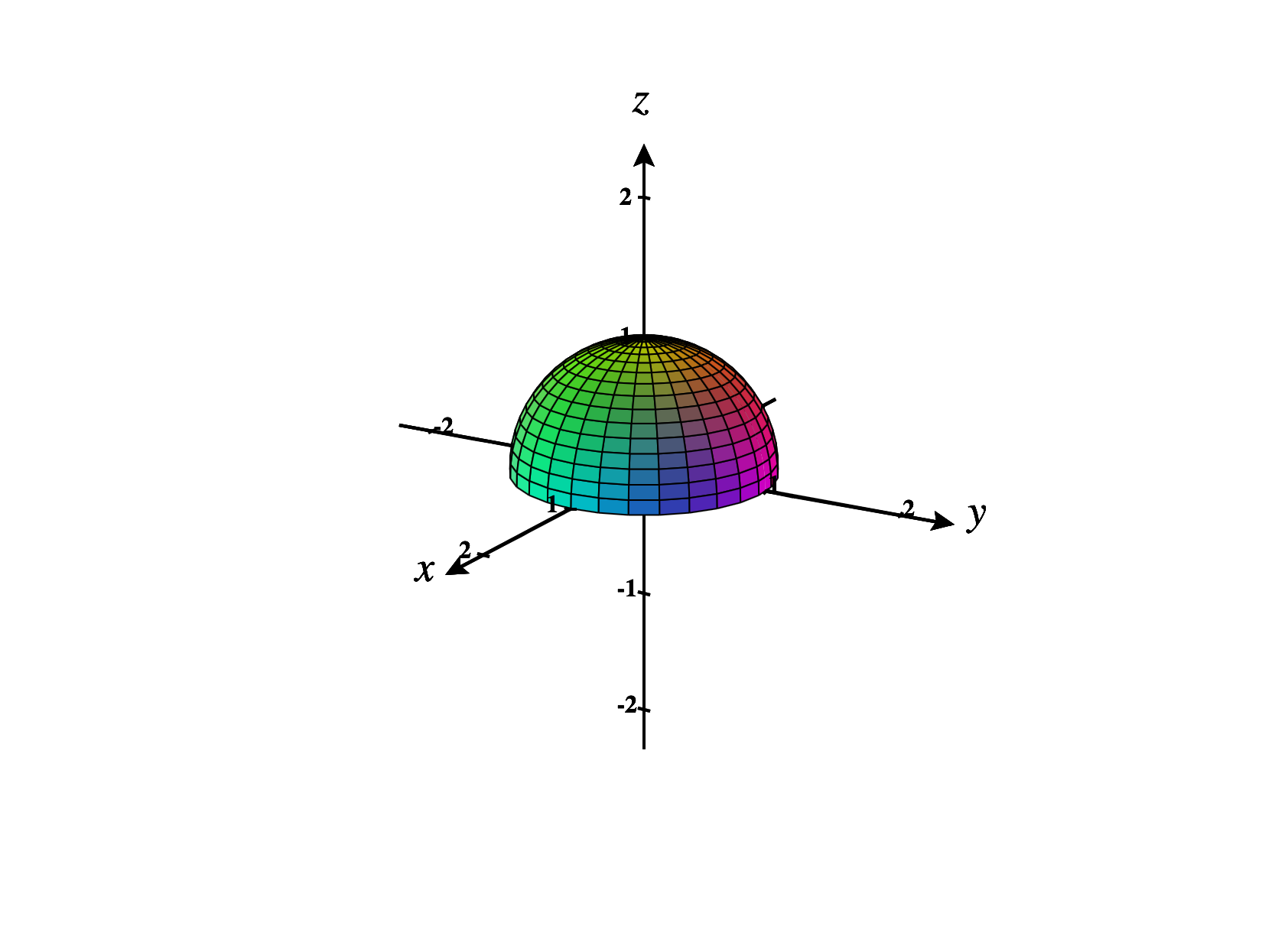
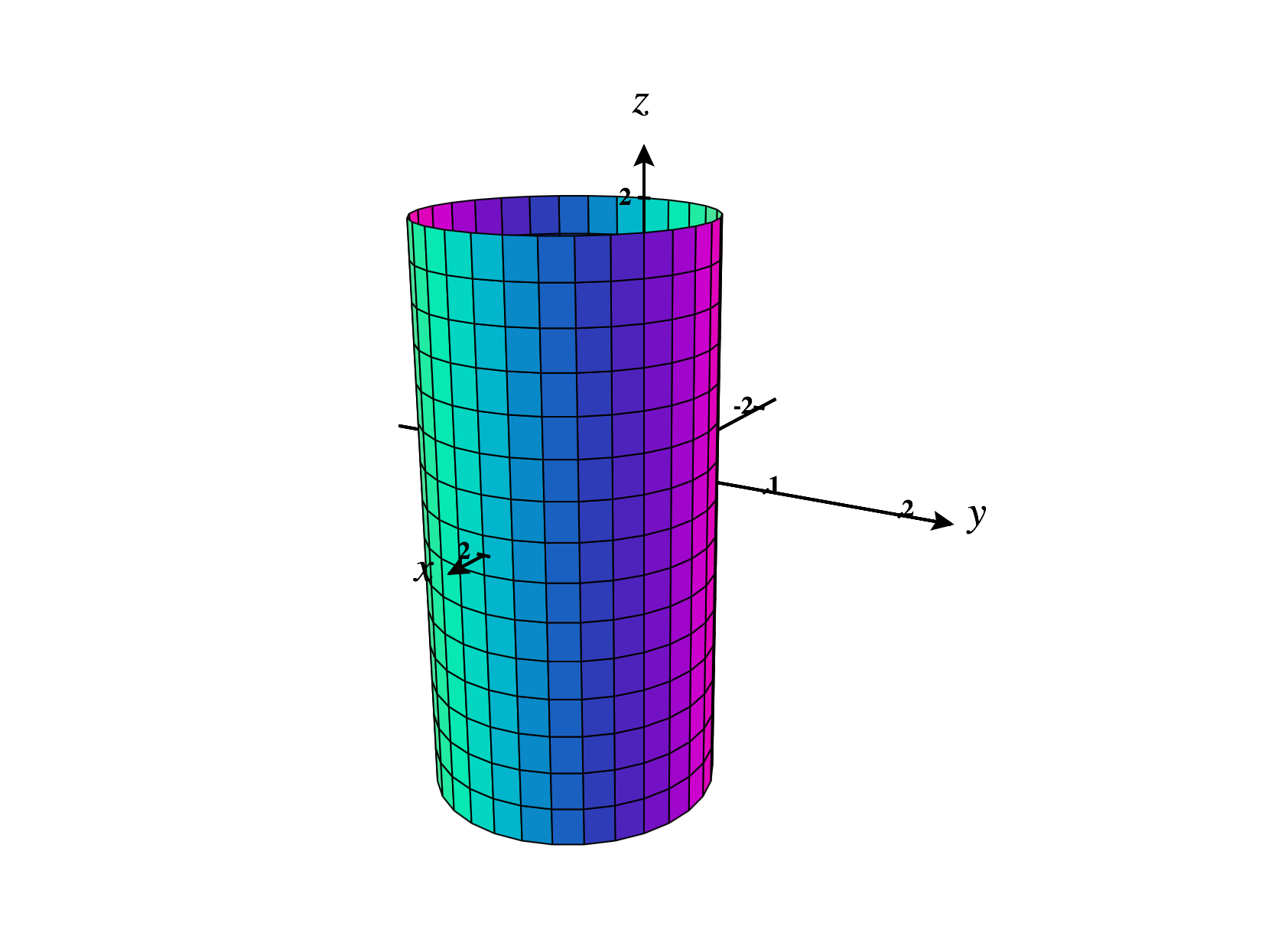
We’ll determine how to describe this cylinder in cylindrical coordinates, by converting the equation to cylindrical coordinates.
Expanding the expression, we have Substituting and subtracting from each side, we obtain We then substitute . Dividing both sides by , we have or and can be anything.
When we divided by , we implicitly assumed that was not . This means that we might accidentally be omitting the origin, but if we take , we have so the origin is already included in the surface .
Images were generated using CalcPlot3D.