Moving Frame Computations

$\newenvironment {prompt}{}{} \newcommand {\DeclareMathOperator }[2]{\@OldDeclareMathOperator {##1}{##2}\immediate \write \myfile {\unexpanded {\DeclareMathOperator }{\unexpanded {##1}}{\unexpanded {##2}}}} \newcommand {\ungraded }[0]{} \newcommand {\reserved@a }[2]{} \newcommand {\HyperFirstAtBeginDocument }[0]{\AtBeginDocument } \newcommand {\reserved@a }[1]{} \newcommand {\reserved@a }[2]{} \newcommand {\vnameref }[1]{\unskip ~\nameref {##1}\@vpageref [\unskip ]{##1}} \newcommand {\ref }[0]{\@ifstar \@refstar \T@ref } \newcommand {\pageref }[0]{\@ifstar \@pagerefstar \T@pageref } \newcommand {\nameref }[0]{\@ifstar \@namerefstar \T@nameref } \newcommand {\reserved@a }[2]{} \newcommand {\reserved@a }[0]{\AtBeginDocument } \newcommand {\reserved@a }[1]{} \newcommand {\reserved@a }[2]{}$

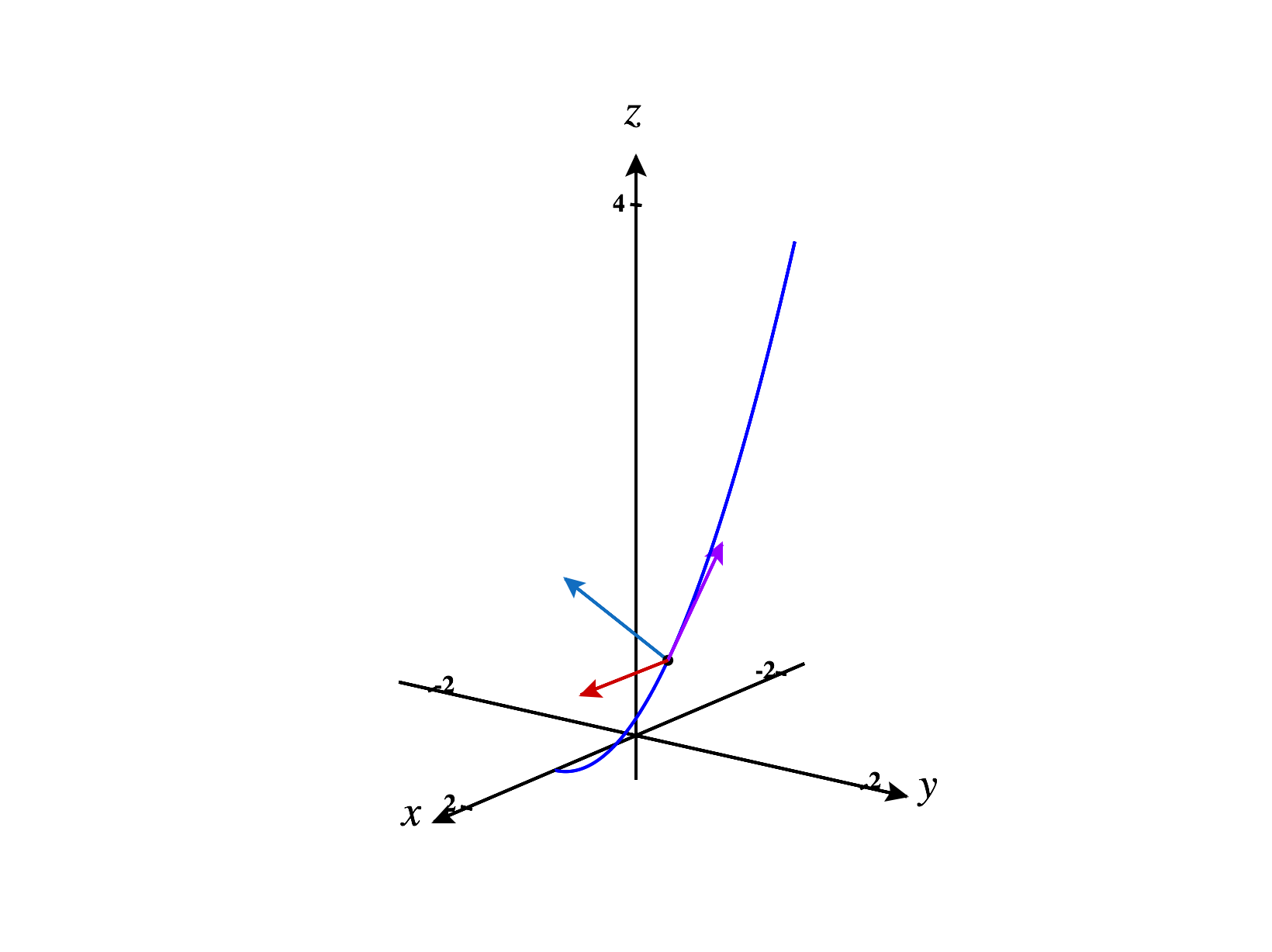
Recall our definition of the moving frame:

Given a path $\vec {x}(t)$ , we define the moving frame of the path to be the triple $(\vec {T},\vec {N},\vec {B})$ .

$\vec {T}$ is the unit tangent vector, $\vec {T}(t) = \dfrac {\vec {x}'(t)}{\|\vec {x}'(t)\|}.$

$\vec {N}$ is the unit normal vector, $\vec {N}(t) = \dfrac {\vec {T}'(t)}{\|\vec {T}'(t)\|}.$

$\vec {B}$ is the unit binormal vector, $\vec {B}(t) = \vec {T}(t)\times \vec {N}(t).$

The moving frame is also called the TNB frame.

We’ll now work through some moving frame computations. These computations can sometimes get quite nasty, so it’s important to simplify as you go, and plug in points when possible.

Examples

We’ll compute the moving frame for the path $\vec {x}(t) = (\cos (t),\sin (t), t)$ in general, and when $t = 0$ .

In order to find the unit tangent vector, we first need to find the velocity vector. $\vec {x}'(t) = \answer {(-\sin (t), \cos (t), 1)}$ Computing the length, we have $\|\vec {x}'(t)\| = \answer {\sqrt {2}}.$ From these, we compute

$\begin{align*} \vec{T}(t) &= \dfrac{\vec{x}'(t)}{\|\vec{x}'(t)\|}\\ &= \answer{(-\frac{1}{\sqrt{2}}\sin(t), \frac{1}{\sqrt{2}}\cos(t), \frac{1}{\sqrt{2}})}. \end{align*}$

Plugging in $t=0$ , we have $\vec {T}(0) = \answer {(0,\frac {1}{\sqrt {2}},\frac {1}{\sqrt {2}})}.$ Next, we need to find the unit binormal vector. For this, we first need to find $\vec {T}'(t)$ . $\vec {T}'(t) = \answer {(-\frac {1}{\sqrt {2}}\cos (t), -\frac {1}{\sqrt {2}}\sin (t), 0)}$ Computing the length, we have $\|\vec {T}'(t)\| = \answer {\frac {1}{\sqrt {2}}}.$ From these, we compute

$\begin{align*} \vec{N}(t) &= \dfrac{\vec{T}'(t)}{\|\vec{T}'(t)\|}\\ &= \answer{(-\cos(t), -\sin(t),0)}. \end{align*}$

Plugging in $t=0$ , we have $\vec {N}(t) = \answer {(-1,0,0)}.$ Finally, we need to find the unit binormal vector.

$\begin{align*} \vec{B}(t) &= \vec{T}(t)\times\vec{N}(t)\\ &= \answer{(\frac{1}{\sqrt{2}}\sin(t), -\frac{1}{\sqrt{2}}\cos(t), \frac{1}{\sqrt{2}})} \end{align*}$

Plugging in $t=0$ , we have $\vec {B}(0) = \answer {(0, \frac {1}{\sqrt {2}}, \frac {1}{\sqrt {2}})}.$

We’ll compute the moving frame for the path $\vec {x}(t) = (1, t, t^2)$ when $t=1$ .

Since we only need the moving frame for one specific value of $t$ , we’ll plug in this value as soon as we can, to help simplify computation. However, we need to make sure that we’ve taken all necessary derivatives before plugging in $t=1$ .

In order to find the unit tangent vector, we first need to find the velocity vector. $\vec {x}'(t) = \answer {(0, 1, 2t)}$ If we only needed to find $\vec {T}(1)$ , we could plug in $t=1$ at this point. However, we will eventually need to differentiate $\vec {T}(t)$ to find $\vec {N}(t)$ , so we’ll hold off on plugging in $t=1$ for now.

Next, we find the length of $\vec {x}'(t)$ . $\|\vec {x}'(t)\| = \answer {\sqrt {1+4t^2}}$

Then, we have that the unit tangent vector is

$\begin{align*} \vec{T}(t) &= \dfrac{\vec{x}'(t)}{\|\vec{x}'(t)\|}\\ &= \answer{(0,\frac{1}{\sqrt{1+4t^2}}, \frac{2t}{\sqrt{1+4t^2}})}. \end{align*}$

Plugging in $t=1$ , we have $\vec {T}(1) = \answer {(0,\frac {1}{\sqrt {5}}, \frac {2}{\sqrt {5}})}.$

Next, we differentiate $\vec {T}(t)$ . Take a moment to revel in gratitude that we’re doing this computation for you. $\vec {T}'(t) = \left (0,\frac {-4t}{(1+4t^2)^{3/2}}, \frac {2}{(1+4t^2)^{3/2}}\right )$ At this point, we don’t have anymore derivatives to take, so we’ll plug in $t=1$ before continuing our computation. $\vec {T}'(1) = \answer {(0,\frac {-4}{5^{3/2}}, \frac {2}{5^{3/2}})}$ The length of this vector is $\|\vec {T}'(1)\| = \answer {2/5}.$ From these, we compute the unit normal vector when $t=1$ ,

$\begin{align*} \vec{N}(1) &= \dfrac{\vec{T}'(1)}{\|\vec{T}'(1)\|}\\ &= \answer{(0,\frac{-2}{\sqrt{5}},\frac{1}{\sqrt{5}})}. \end{align*}$

Finally, we compute the unit binormal vector when $t=1$ .

$\begin{align*} \vec{B}(1) &= \vec{T}(1)\times\vec{N}(1)\\ &= \answer{(1,0,0)} \end{align*}$

Notice how helpful it was to plug in $t=1$ as early as we could!

Images were generated using CalcPlot3D.