Describing regions

$\newenvironment {prompt}{}{} \newcommand {\ungraded }[0]{} \newcommand {\todo }[0]{} \newcommand {\oiint }[0]{{\large \bigcirc }\kern -1.56em\iint } \newcommand {\mooculus }[0]{\textsf {\textbf {MOOC}\textnormal {\textsf {ULUS}}}} \newcommand {\npnoround }[0]{\nprounddigits {-1}} \newcommand {\npnoroundexp }[0]{\nproundexpdigits {-1}} \newcommand {\npunitcommand }[1]{\ensuremath {\mathrm {#1}}} \newcommand {\RR }[0]{\mathbb R} \newcommand {\R }[0]{\mathbb R} \newcommand {\N }[0]{\mathbb N} \newcommand {\Z }[0]{\mathbb Z} \newcommand {\sagemath }[0]{\textsf {SageMath}} \newcommand {\d }[0]{\,d} \newcommand {\l }[0]{\ell } \newcommand {\ddx }[0]{\frac {d}{\d x}} \newcommand {\zeroOverZero }[0]{\ensuremath {\boldsymbol {\tfrac {0}{0}}}} \newcommand {\inftyOverInfty }[0]{\ensuremath {\boldsymbol {\tfrac {\infty }{\infty }}}} \newcommand {\zeroOverInfty }[0]{\ensuremath {\boldsymbol {\tfrac {0}{\infty }}}} \newcommand {\zeroTimesInfty }[0]{\ensuremath {\small \boldsymbol {0\cdot \infty }}} \newcommand {\inftyMinusInfty }[0]{\ensuremath {\small \boldsymbol {\infty -\infty }}} \newcommand {\oneToInfty }[0]{\ensuremath {\boldsymbol {1^\infty }}} \newcommand {\zeroToZero }[0]{\ensuremath {\boldsymbol {0^0}}} \newcommand {\inftyToZero }[0]{\ensuremath {\boldsymbol {\infty ^0}}} \newcommand {\numOverZero }[0]{\ensuremath {\boldsymbol {\tfrac {\#}{0}}}} \newcommand {\dfn }[0]{\textbf } \newcommand {\unit }[0]{\mathop {}\!\mathrm } \newcommand {\eval }[1]{\bigg [ #1 \bigg ]} \newcommand {\seq }[1]{\left ( #1 \right )} \newcommand {\epsilon }[0]{\varepsilon } \newcommand {\phi }[0]{\varphi } \newcommand {\iff }[0]{\Leftrightarrow } \DeclareMathOperator {\arccot }{arccot} \DeclareMathOperator {\arcsec }{arcsec} \DeclareMathOperator {\arccsc }{arccsc} \DeclareMathOperator {\si }{Si} \DeclareMathOperator {\scal }{scal} \DeclareMathOperator {\sign }{sign} \newcommand {\arrowvec }[1]{{\overset {\rightharpoonup }{#1}}} \newcommand {\vec }[1]{{\overset {\boldsymbol {\rightharpoonup }}{\mathbf {#1}}}\hspace {0in}} \newcommand {\point }[1]{\left (#1\right )} \newcommand {\pt }[1]{\mathbf {#1}} \newcommand {\Lim }[2]{\lim _{\point {#1} \to \point {#2}}} \DeclareMathOperator {\proj }{\mathbf {proj}} \newcommand {\veci }[0]{{\boldsymbol {\hat {\imath }}}} \newcommand {\vecj }[0]{{\boldsymbol {\hat {\jmath }}}} \newcommand {\veck }[0]{{\boldsymbol {\hat {k}}}} \newcommand {\vecl }[0]{\vec {\boldsymbol {\l }}} \newcommand {\uvec }[1]{\mathbf {\hat {#1}}} \newcommand {\utan }[0]{\mathbf {\hat {t}}} \newcommand {\unormal }[0]{\mathbf {\hat {n}}} \newcommand {\ubinormal }[0]{\mathbf {\hat {b}}} \newcommand {\dotp }[0]{\bullet } \newcommand {\cross }[0]{\boldsymbol \times } \newcommand {\grad }[0]{\boldsymbol \nabla } \newcommand {\divergence }[0]{\grad \dotp } \newcommand {\curl }[0]{\grad \cross } \newcommand {\lto }[0]{\mathop {\longrightarrow \,}\limits } \newcommand {\bar }[0]{\overline } \newcommand {\surfaceColor }[0]{violet} \newcommand {\surfaceColorTwo }[0]{redyellow} \newcommand {\sliceColor }[0]{greenyellow} \newcommand {\vector }[1]{\left \langle #1\right \rangle } \newcommand {\sectionOutcomes }[0]{} \newcommand {\HyperFirstAtBeginDocument }[0]{\AtBeginDocument }$

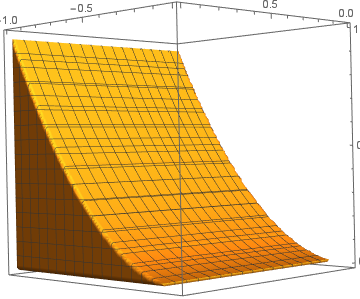
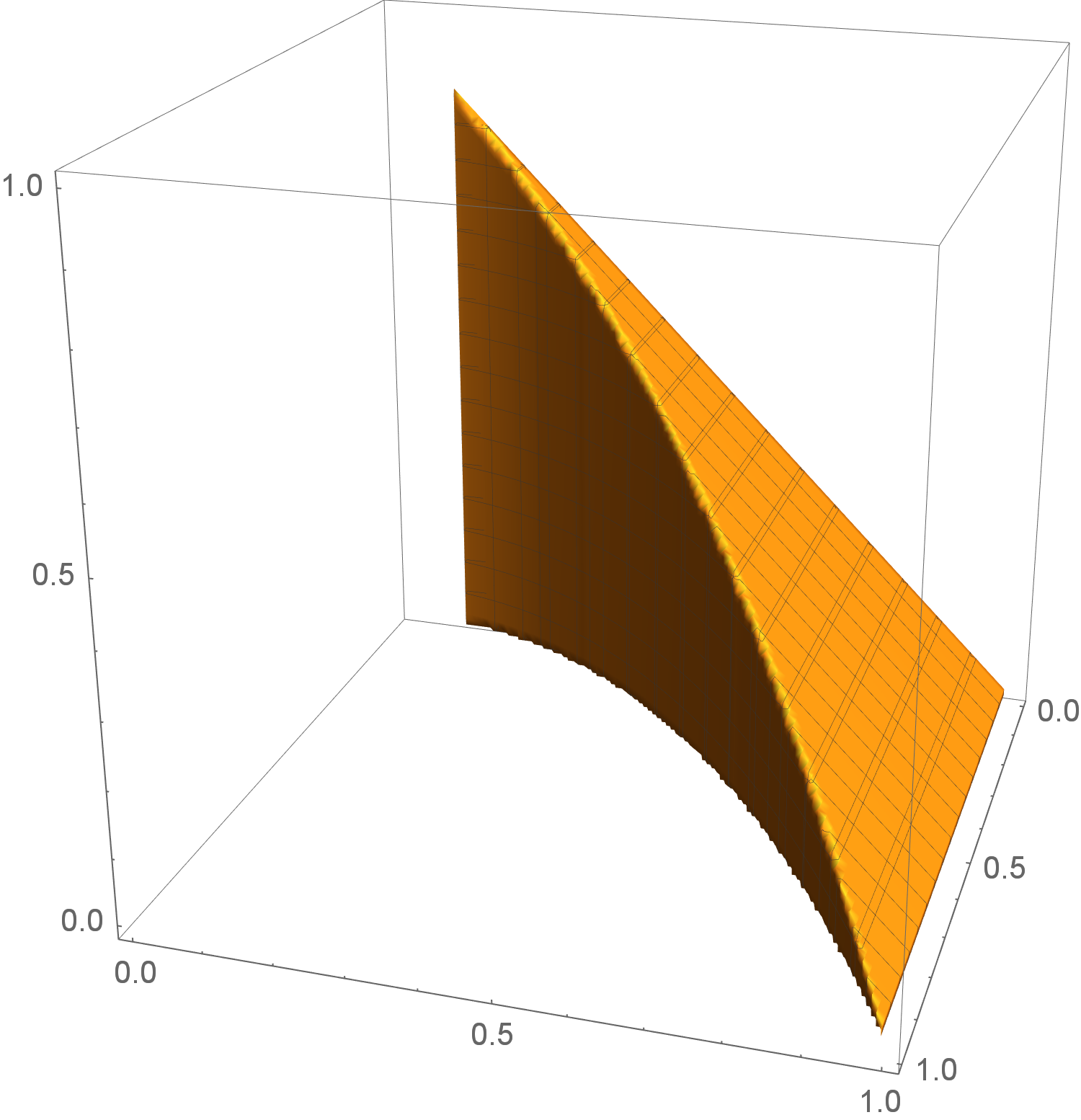
We describe areas and volumes of regions using iterated integrals.

Work in groups of 3–4, writing your answers on a separate sheet of paper.

Trivial regions

Without doing any integrals, evaluate $\iint _R \d A$ where $R =\{(x,y):-2\le x\le 4 \text { and } -6\le y\le 1\}.$

Without doing any integrals, evaluate $\iiint _R \d V$ where $R =\{(x,y,z):-4\le x\le 3, -1\le y\le 5,\text { and, } -3\le z\le 2\}.$

Two-dimensional regions

Consider the region $R=\{(x,y):0\le x\le 2+\cos (y)\text { and }0<y<2\pi \}$

Compute the area of this region with an iterated integral where one integrates first with respect to $x$ and next integrates with respect to $y$ .

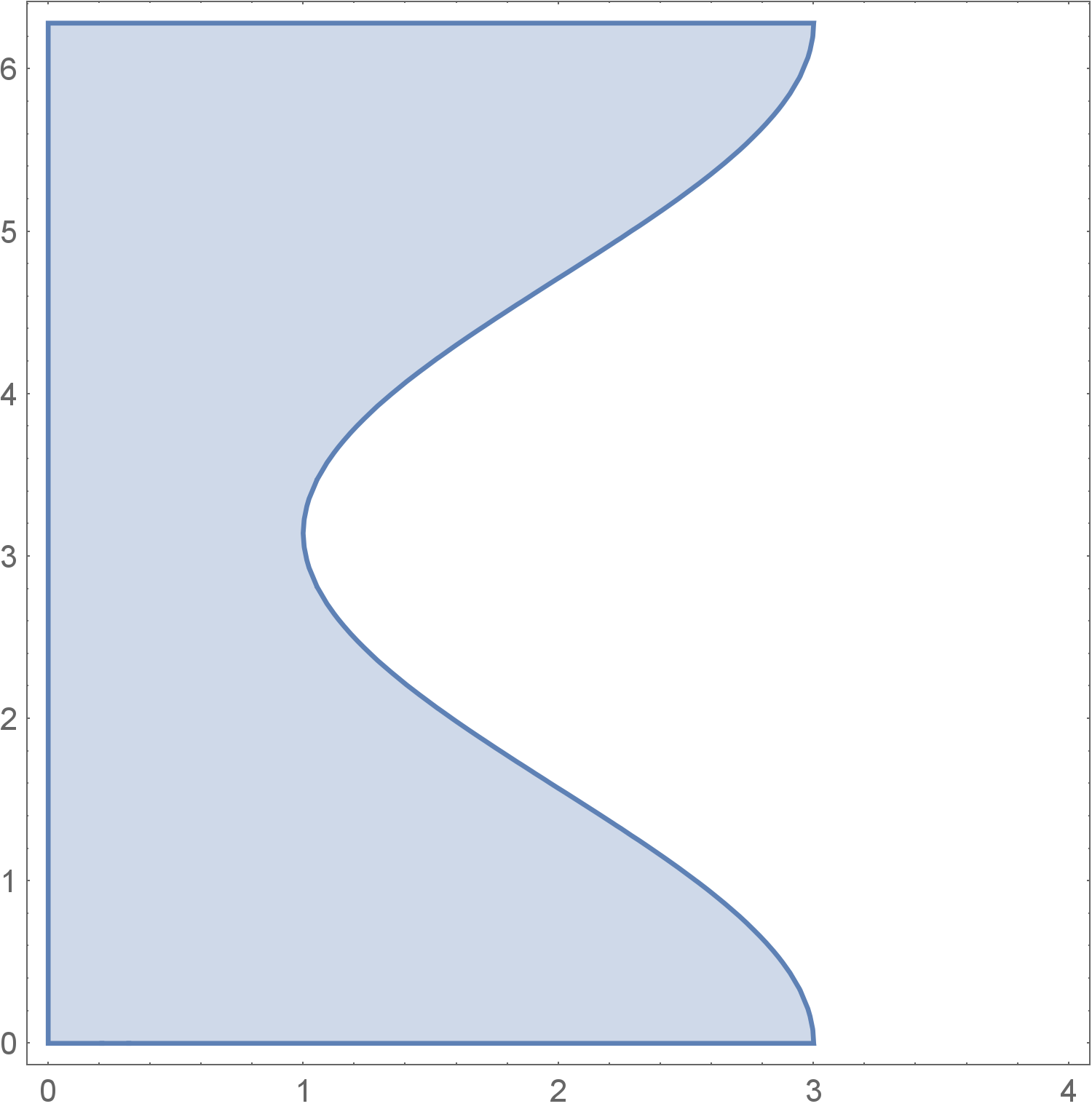
As a challenge, compute the area with an iterated integral where one integrates first with respect to $y$ and next integrates with respect to $x$ .

Consider the region

(a): Compute the area of this region with an iterated integral where one integrates first with respect to $y$ and next integrates with respect to $x$ .
(b): Compute the area of this region with an iterated integral where one integrates first with respect to $x$ and next integrates with respect to $y$ .

Consider the ellipse centered at the origin:

Recall that the implicit formula for an ellipse is given by $\left (\frac {x-x_0}{a}\right )^2 + \left (\frac {y-y_0}{b}\right )^2 = 1.$

(a): Compute the area of this region with an iterated integral where one integrates first with respect to $y$ and next integrates with respect to $x$ .
(b): Compute the area of this region with an iterated integral where one integrates first with respect to $x$ and next integrates with respect to $y$ .

Consider the following region:

The largest $y$ -value of the region is $y=\sqrt {2}$ .

(a): Compute the area of this region with an iterated integral where one integrates first with respect to $y$ and next integrates with respect to $x$ .
(b): Compute the area of this region with an iterated integral where one integrates first with respect to $x$ and next integrates with respect to $y$ .

Three-dimensional regions

Consider the region bounded by the planes:

$x=0$
$y=0$
$z=0$
$6x+3y+2z = 24$

Sketch this region and set-up six iterated integrals that compute the volume of this solid, all which integrate in a different order.

Consider the region: $R=\{(x,y,z): 0 \le x \le 1, -1\le y \le 0, 0\le z\le y^2\}$

Set up six iterated integrals that compute the volume of this solid, all which integrate in a different order.

Consider the region: $R=\{(x,y,z): 0 \le x \le 1, \sqrt {x}\le y \le 1, 0\le z\le 1-y\}$

Set up six iterated integrals that compute the volume of this solid, all which integrate in a different order.