Input impedance of a transmission line

$\newenvironment {prompt}{}{} \newcommand {\ungraded }[0]{} \newcommand {\todo }[0]{} \newcommand {\oiint }[0]{{\large \bigcirc }\kern -1.56em\iint } \newcommand {\mooculus }[0]{\textsf {\textbf {MOOC}\textnormal {\textsf {ULUS}}}} \newcommand {\npnoround }[0]{\nprounddigits {-1}} \newcommand {\npnoroundexp }[0]{\nproundexpdigits {-1}} \newcommand {\npunitcommand }[1]{\ensuremath {\mathrm {#1}}} \newcommand {\RR }[0]{\mathbb R} \newcommand {\R }[0]{\mathbb R} \newcommand {\N }[0]{\mathbb N} \newcommand {\Z }[0]{\mathbb Z} \newcommand {\sagemath }[0]{\textsf {SageMath}} \newcommand {\d }[0]{\mathop {}\!d} \newcommand {\l }[0]{\ell } \newcommand {\ddx }[0]{\frac {d}{\d x}} \newcommand {\zeroOverZero }[0]{\ensuremath {\boldsymbol {\tfrac {0}{0}}}} \newcommand {\inftyOverInfty }[0]{\ensuremath {\boldsymbol {\tfrac {\infty }{\infty }}}} \newcommand {\zeroOverInfty }[0]{\ensuremath {\boldsymbol {\tfrac {0}{\infty }}}} \newcommand {\zeroTimesInfty }[0]{\ensuremath {\small \boldsymbol {0\cdot \infty }}} \newcommand {\inftyMinusInfty }[0]{\ensuremath {\small \boldsymbol {\infty -\infty }}} \newcommand {\oneToInfty }[0]{\ensuremath {\boldsymbol {1^\infty }}} \newcommand {\zeroToZero }[0]{\ensuremath {\boldsymbol {0^0}}} \newcommand {\inftyToZero }[0]{\ensuremath {\boldsymbol {\infty ^0}}} \newcommand {\numOverZero }[0]{\ensuremath {\boldsymbol {\tfrac {\#}{0}}}} \newcommand {\dfn }[0]{\textbf } \newcommand {\unit }[0]{\mathop {}\!\mathrm } \newcommand {\eval }[1]{\bigg [ #1 \bigg ]} \newcommand {\seq }[1]{\left ( #1 \right )} \newcommand {\epsilon }[0]{\varepsilon } \newcommand {\phi }[0]{\varphi } \newcommand {\iff }[0]{\Leftrightarrow } \DeclareMathOperator {\arccot }{arccot} \DeclareMathOperator {\arcsec }{arcsec} \DeclareMathOperator {\arccsc }{arccsc} \DeclareMathOperator {\si }{Si} \DeclareMathOperator {\scal }{scal} \DeclareMathOperator {\sign }{sign} \newcommand {\arrowvec }[1]{{\overset {\rightharpoonup }{#1}}} \newcommand {\vec }[1]{{\overset {\boldsymbol {\rightharpoonup }}{\mathbf {#1}}}\hspace {0in}} \newcommand {\point }[1]{\left (#1\right )} \newcommand {\pt }[1]{\mathbf {#1}} \newcommand {\Lim }[2]{\lim _{\point {#1} \to \point {#2}}} \DeclareMathOperator {\proj }{\mathbf {proj}} \newcommand {\veci }[0]{{\boldsymbol {\hat {\imath }}}} \newcommand {\vecj }[0]{{\boldsymbol {\hat {\jmath }}}} \newcommand {\veck }[0]{{\boldsymbol {\hat {k}}}} \newcommand {\vecl }[0]{\vec {\boldsymbol {\l }}} \newcommand {\uvec }[1]{\mathbf {\hat {#1}}} \newcommand {\utan }[0]{\mathbf {\hat {t}}} \newcommand {\unormal }[0]{\mathbf {\hat {n}}} \newcommand {\ubinormal }[0]{\mathbf {\hat {b}}} \newcommand {\dotp }[0]{\bullet } \newcommand {\cross }[0]{\boldsymbol \times } \newcommand {\grad }[0]{\boldsymbol \nabla } \newcommand {\divergence }[0]{\grad \dotp } \newcommand {\curl }[0]{\grad \cross } \newcommand {\lto }[0]{\mathop {\longrightarrow \,}\limits } \newcommand {\bar }[0]{\overline } \newcommand {\surfaceColor }[0]{violet} \newcommand {\surfaceColorTwo }[0]{redyellow} \newcommand {\sliceColor }[0]{greenyellow} \newcommand {\vector }[1]{\left \langle #1\right \rangle } \newcommand {\sectionOutcomes }[0]{} \newcommand {\HyperFirstAtBeginDocument }[0]{\AtBeginDocument }$

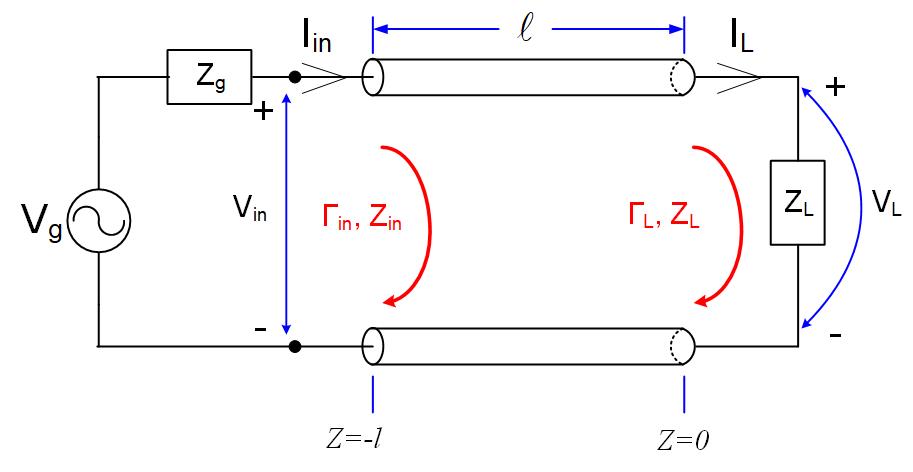
Again, we will look at a transmission line circuit in Figure fig:IITRLine to find the input impedance on a transmission line.

Figure 1: Transmission Line connects generator and the load.

The equations for the voltage and current anywhere (any z) on a transmission line are

$\begin{eqnarray} \tilde{V}(z)= \tilde{V}_0^+ (e^{j \beta z} + \Gamma_L e^{-j \beta z } ) \label{eq:vtlfin} \\ I(z)= \frac{\tilde{V}_0^+}{Z_0} (e^{j \beta z} - \Gamma e^{-j \beta z} ) \label{eq:itlfin} \end{eqnarray}$

The voltage and current equations at the generator $z=-l$ are:

$\begin{eqnarray} \tilde{V}_{in}=\tilde{V}(z=-l)= \tilde{V}_0^+ (e^{j \beta l} + \Gamma_L e^{-j \beta l } ) \\ \tilde{I}_{in}=I(z=-l)= \frac{\tilde{V}_0^+}{Z_0} (e^{j \beta l} - \Gamma e^{-j \beta l} ) \end{eqnarray}$

Input impedance as a function of reflection coefficient

The input impedance is defined as $Z_{in}=\frac {V_{in}}{I_{in}}$ . Since the line length is $l$ , the input impedance is

$\begin{eqnarray} Z_{in}=\frac{\tilde{V}_0^+ (e^{-j \beta z} + \Gamma_L e^{j \beta z } )}{\frac{\tilde{V}_0^+}{Z_0} (e^{-j \beta z} - \Gamma_L e^{j \beta z} )} \end{eqnarray}$

If we cancel common terms, we get

$\begin{eqnarray} Z_{in}=Z_0 \frac{(e^{-j \beta z} + \Gamma_L e^{j \beta z } )}{ (e^{-j \beta z} - \Gamma_L e^{j \beta z} )} \label{eq:theSecondway} \end{eqnarray}$

Now we can take $e^{-j \beta z}$ in front of parenthesis from both numerator and denominator and then cancel it.

$\begin{eqnarray} Z_{in}=Z_0 \frac{1 + \Gamma_L e^{ 2j \beta z } }{ 1 - \Gamma_L e^{2j \beta z} } \end{eqnarray}$

We have previously defined the reflection coefficient at the transmission line’s input as $\Gamma _{in}=\Gamma _L e^{ 2 j \beta z }$ . The final equation for the input impedance is therefore

$\begin{eqnarray} Z_{in}=Z_0 \frac{1 + \Gamma_{in} }{ 1 - \Gamma_{in} } \end{eqnarray}$

Input impedance as a function of load impedance

If we now look back at the Equation eq:theSecondway, here we can also use Euler’s formula $e^{j \beta z} = \cos (\beta z) + j\sin (\beta z)$ , and the equation for the reflection coefficient at the load $\Gamma _L = \frac {Z_L-Z_0}{Z_L+Z_0}$ we find the input impedance of the line as shown below.

$\begin{eqnarray} Z_{in}= Z_0 \frac{Z_L+ j Z_0 \tan \beta l}{Z_0+ j Z_L \tan \beta l} \end{eqnarray}$

This equation will be soon become obsolete when we learn how to use the Smith Chart.

Find the input impedance if the load impedance is $Z_L=0 \Omega$ , and the electrical length of the line is $\beta l = 90^0$ .

Since the load impedance is a short circuit, and the angle is $90^0$ the equation simplifies to $Z_{in}= j Z_0 \tan \beta l = \infty$ .

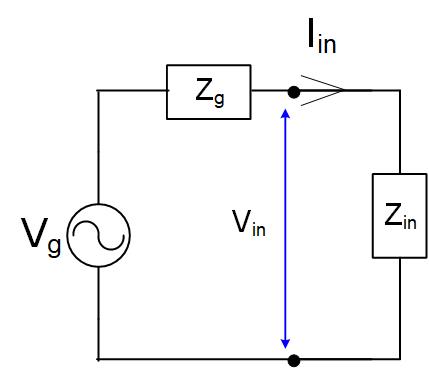
When we find the input impedance, we can replace the transmission line and the load, as shown in Figure fig:IITRLineEqCirc. In the next section, we will use input impedance to find the forward going voltage on a transmission line.

Figure 2: Transmission Line connects generator and the load.