Smith Chart

$\newenvironment {prompt}{}{} \newcommand {\ungraded }[0]{} \newcommand {\todo }[0]{} \newcommand {\oiint }[0]{{\large \bigcirc }\kern -1.56em\iint } \newcommand {\mooculus }[0]{\textsf {\textbf {MOOC}\textnormal {\textsf {ULUS}}}} \newcommand {\npnoround }[0]{\nprounddigits {-1}} \newcommand {\npnoroundexp }[0]{\nproundexpdigits {-1}} \newcommand {\npunitcommand }[1]{\ensuremath {\mathrm {#1}}} \newcommand {\RR }[0]{\mathbb R} \newcommand {\R }[0]{\mathbb R} \newcommand {\N }[0]{\mathbb N} \newcommand {\Z }[0]{\mathbb Z} \newcommand {\sagemath }[0]{\textsf {SageMath}} \newcommand {\d }[0]{\mathop {}\!d} \newcommand {\l }[0]{\ell } \newcommand {\ddx }[0]{\frac {d}{\d x}} \newcommand {\zeroOverZero }[0]{\ensuremath {\boldsymbol {\tfrac {0}{0}}}} \newcommand {\inftyOverInfty }[0]{\ensuremath {\boldsymbol {\tfrac {\infty }{\infty }}}} \newcommand {\zeroOverInfty }[0]{\ensuremath {\boldsymbol {\tfrac {0}{\infty }}}} \newcommand {\zeroTimesInfty }[0]{\ensuremath {\small \boldsymbol {0\cdot \infty }}} \newcommand {\inftyMinusInfty }[0]{\ensuremath {\small \boldsymbol {\infty -\infty }}} \newcommand {\oneToInfty }[0]{\ensuremath {\boldsymbol {1^\infty }}} \newcommand {\zeroToZero }[0]{\ensuremath {\boldsymbol {0^0}}} \newcommand {\inftyToZero }[0]{\ensuremath {\boldsymbol {\infty ^0}}} \newcommand {\numOverZero }[0]{\ensuremath {\boldsymbol {\tfrac {\#}{0}}}} \newcommand {\dfn }[0]{\textbf } \newcommand {\unit }[0]{\mathop {}\!\mathrm } \newcommand {\eval }[1]{\bigg [ #1 \bigg ]} \newcommand {\seq }[1]{\left ( #1 \right )} \newcommand {\epsilon }[0]{\varepsilon } \newcommand {\phi }[0]{\varphi } \newcommand {\iff }[0]{\Leftrightarrow } \DeclareMathOperator {\arccot }{arccot} \DeclareMathOperator {\arcsec }{arcsec} \DeclareMathOperator {\arccsc }{arccsc} \DeclareMathOperator {\si }{Si} \DeclareMathOperator {\scal }{scal} \DeclareMathOperator {\sign }{sign} \newcommand {\arrowvec }[1]{{\overset {\rightharpoonup }{#1}}} \newcommand {\vec }[1]{{\overset {\boldsymbol {\rightharpoonup }}{\mathbf {#1}}}\hspace {0in}} \newcommand {\point }[1]{\left (#1\right )} \newcommand {\pt }[1]{\mathbf {#1}} \newcommand {\Lim }[2]{\lim _{\point {#1} \to \point {#2}}} \DeclareMathOperator {\proj }{\mathbf {proj}} \newcommand {\veci }[0]{{\boldsymbol {\hat {\imath }}}} \newcommand {\vecj }[0]{{\boldsymbol {\hat {\jmath }}}} \newcommand {\veck }[0]{{\boldsymbol {\hat {k}}}} \newcommand {\vecl }[0]{\vec {\boldsymbol {\l }}} \newcommand {\uvec }[1]{\mathbf {\hat {#1}}} \newcommand {\utan }[0]{\mathbf {\hat {t}}} \newcommand {\unormal }[0]{\mathbf {\hat {n}}} \newcommand {\ubinormal }[0]{\mathbf {\hat {b}}} \newcommand {\dotp }[0]{\bullet } \newcommand {\cross }[0]{\boldsymbol \times } \newcommand {\grad }[0]{\boldsymbol \nabla } \newcommand {\divergence }[0]{\grad \dotp } \newcommand {\curl }[0]{\grad \cross } \newcommand {\lto }[0]{\mathop {\longrightarrow \,}\limits } \newcommand {\bar }[0]{\overline } \newcommand {\surfaceColor }[0]{violet} \newcommand {\surfaceColorTwo }[0]{redyellow} \newcommand {\sliceColor }[0]{greenyellow} \newcommand {\vector }[1]{\left \langle #1\right \rangle } \newcommand {\sectionOutcomes }[0]{} \newcommand {\HyperFirstAtBeginDocument }[0]{\AtBeginDocument }$

Smith Chart is a handy tool that we use to visualize impedances and reflection coefficients. Lumped element and transmission line impedance matching would be challenging to understand without Smith Charts. Simulation software such as ADS and measurement equipment, such as Network Analyzers, use Smith Chart to represent simulated or measured data. Smith Chart first looks like Black Magic, but it is a straightforward and useful tool that will help us better understand impedance/admittance transformations and transmission lines.

Smith Chart is a polar plot of the reflection coefficient.

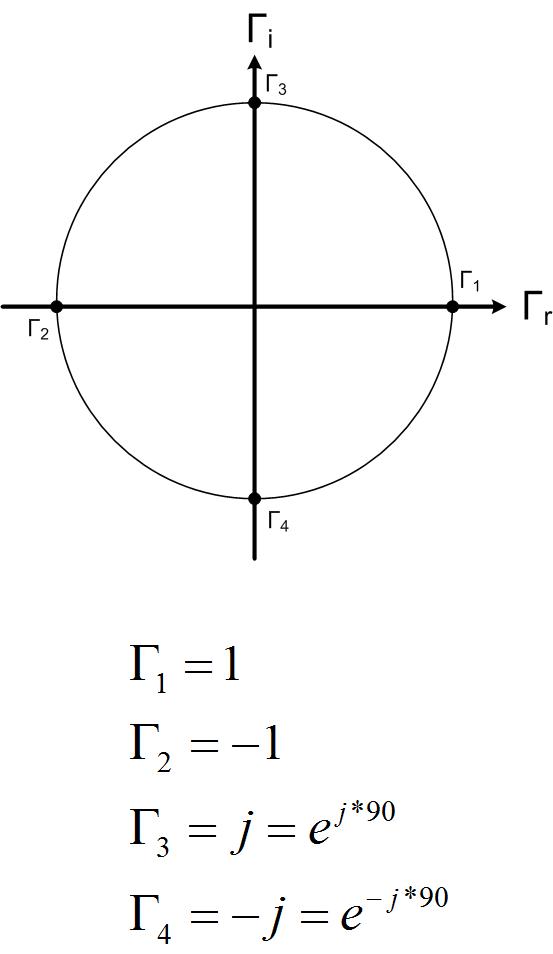
An example of a Smith Chart is given in Figure fig:SC1

Figure 1: Smith Chart

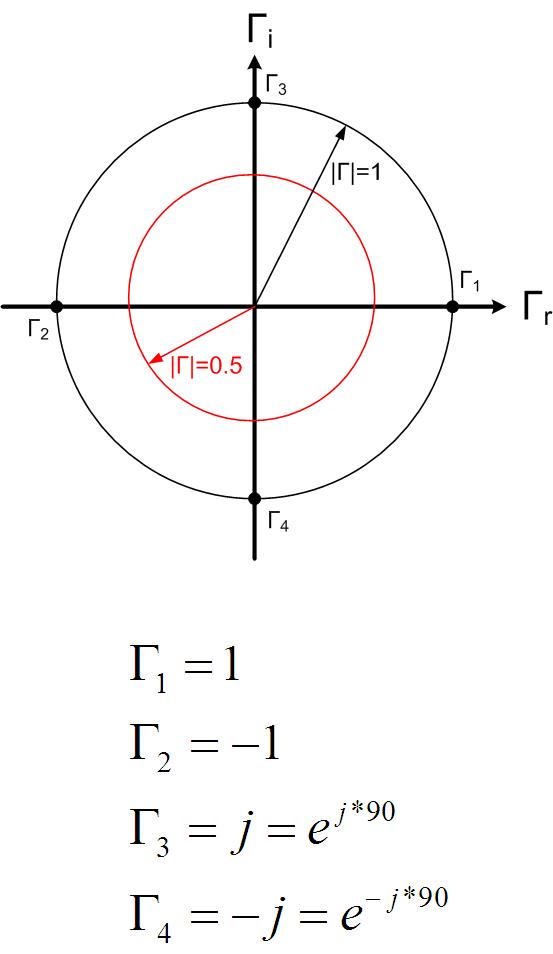
In essence, Smith Chart is a unit circle centered at the origin with a radius of 1. Smith Chart is used to represent the reflection coefficient graphically in polar coordinates. The reflection coefficient’s real and imaginary axis (the Cartesian coordinates) is not shown on the actual Smith Chart. However, the center of the Smith Chart is where the origin of the coordinate system would be. We usually represent the reflection coefficient in polar coordinates, with a magnitude and an angle. Magnitude is the distance between the point and the origin, and the angle is measured from the x-axis. An example location of several reflection coefficients is given in Figure scex. If you do not see why the points are positioned as shown, review the polar representation of complex numbers.

Figure 2: Examples of location of reflection coefficient on the Smith Chart.

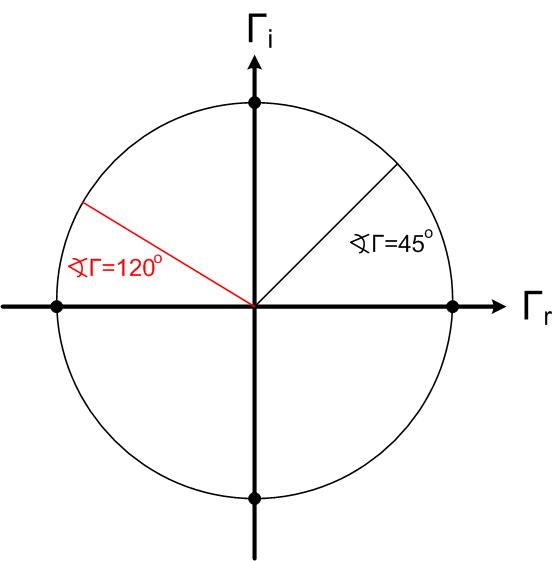
Figure scswr1, scswr circle and line represent all points on the Smith Chart that have constant magnitude or angle of the reflection coefficient. It is challenging to measure impedances directly at high frequencies, as it is difficult to measure (or sometimes even define) voltage and current. To measure impedances, engineers use Network Analyzer shown in Figure hp8510.

Figure 3: Points of constant magnitude of the reflection coefficient. $| \Gamma |$ =0.5, $| \Gamma |$ =1

Figure 4: Points of constant phase of the reflection coefficient. $< \Gamma =45^\circ$ , $< \Gamma = 120^\circ$

Figure 5: HP8510 Network Analyzer in Microwave Laboratory measures impedances up to 26.5GHz. This piece of equipment is on permanent loan curtesy of Defense Micro Electronic Activity (DMEA), Sacramento

We can estimate the reflection coefficient by looking at the position of a point on the Smith Chart. We know that the radius of the circle is 1. So, if the point is half-way between the center and the perimeter, we know the magnitude of the reflection coefficient is 0.5. We can also estimate the angle of the reflection coefficient. For example, if the magnitude is in the first quadrant, we know that the angle is between $0^0$ and $90^0$ . If the point is on the positive y-axis, we know that the angle is equal to $90^0$ . Observe the simulation below and see if you can estimate the reflection coefficient’s magnitude and angle by looking at the point’s position.

The simulation below shows only positive angles. In practice, if the point is below the x-axis, we use negative angles to describe the angle of the reflection coefficient. For example, if the point is at the negative y-axis, we would say that the reflection coefficient’s angle is $-90^0$ .