Kirchoff’s Laws

$\newenvironment {prompt}{}{} \newcommand {\ungraded }[0]{} \newcommand {\todo }[0]{} \newcommand {\oiint }[0]{{\large \bigcirc }\kern -1.56em\iint } \newcommand {\mooculus }[0]{\textsf {\textbf {MOOC}\textnormal {\textsf {ULUS}}}} \newcommand {\npnoround }[0]{\nprounddigits {-1}} \newcommand {\npnoroundexp }[0]{\nproundexpdigits {-1}} \newcommand {\npunitcommand }[1]{\ensuremath {\mathrm {#1}}} \newcommand {\RR }[0]{\mathbb R} \newcommand {\R }[0]{\mathbb R} \newcommand {\N }[0]{\mathbb N} \newcommand {\Z }[0]{\mathbb Z} \newcommand {\sagemath }[0]{\textsf {SageMath}} \newcommand {\d }[0]{\mathop {}\!d} \newcommand {\l }[0]{\ell } \newcommand {\ddx }[0]{\frac {d}{\d x}} \newcommand {\zeroOverZero }[0]{\ensuremath {\boldsymbol {\tfrac {0}{0}}}} \newcommand {\inftyOverInfty }[0]{\ensuremath {\boldsymbol {\tfrac {\infty }{\infty }}}} \newcommand {\zeroOverInfty }[0]{\ensuremath {\boldsymbol {\tfrac {0}{\infty }}}} \newcommand {\zeroTimesInfty }[0]{\ensuremath {\small \boldsymbol {0\cdot \infty }}} \newcommand {\inftyMinusInfty }[0]{\ensuremath {\small \boldsymbol {\infty -\infty }}} \newcommand {\oneToInfty }[0]{\ensuremath {\boldsymbol {1^\infty }}} \newcommand {\zeroToZero }[0]{\ensuremath {\boldsymbol {0^0}}} \newcommand {\inftyToZero }[0]{\ensuremath {\boldsymbol {\infty ^0}}} \newcommand {\numOverZero }[0]{\ensuremath {\boldsymbol {\tfrac {\#}{0}}}} \newcommand {\dfn }[0]{\textbf } \newcommand {\unit }[0]{\mathop {}\!\mathrm } \newcommand {\eval }[1]{\bigg [ #1 \bigg ]} \newcommand {\seq }[1]{\left ( #1 \right )} \newcommand {\epsilon }[0]{\varepsilon } \newcommand {\phi }[0]{\varphi } \newcommand {\iff }[0]{\Leftrightarrow } \DeclareMathOperator {\arccot }{arccot} \DeclareMathOperator {\arcsec }{arcsec} \DeclareMathOperator {\arccsc }{arccsc} \DeclareMathOperator {\si }{Si} \DeclareMathOperator {\scal }{scal} \DeclareMathOperator {\sign }{sign} \newcommand {\arrowvec }[1]{{\overset {\rightharpoonup }{#1}}} \newcommand {\vec }[1]{{\overset {\boldsymbol {\rightharpoonup }}{\mathbf {#1}}}\hspace {0in}} \newcommand {\point }[1]{\left (#1\right )} \newcommand {\pt }[1]{\mathbf {#1}} \newcommand {\Lim }[2]{\lim _{\point {#1} \to \point {#2}}} \DeclareMathOperator {\proj }{\mathbf {proj}} \newcommand {\veci }[0]{{\boldsymbol {\hat {\imath }}}} \newcommand {\vecj }[0]{{\boldsymbol {\hat {\jmath }}}} \newcommand {\veck }[0]{{\boldsymbol {\hat {k}}}} \newcommand {\vecl }[0]{\vec {\boldsymbol {\l }}} \newcommand {\uvec }[1]{\mathbf {\hat {#1}}} \newcommand {\utan }[0]{\mathbf {\hat {t}}} \newcommand {\unormal }[0]{\mathbf {\hat {n}}} \newcommand {\ubinormal }[0]{\mathbf {\hat {b}}} \newcommand {\dotp }[0]{\bullet } \newcommand {\cross }[0]{\boldsymbol \times } \newcommand {\grad }[0]{\boldsymbol \nabla } \newcommand {\divergence }[0]{\grad \dotp } \newcommand {\curl }[0]{\grad \cross } \newcommand {\lto }[0]{\mathop {\longrightarrow \,}\limits } \newcommand {\bar }[0]{\overline } \newcommand {\surfaceColor }[0]{violet} \newcommand {\surfaceColorTwo }[0]{redyellow} \newcommand {\sliceColor }[0]{greenyellow} \newcommand {\vector }[1]{\left \langle #1\right \rangle } \newcommand {\sectionOutcomes }[0]{} \newcommand {\HyperFirstAtBeginDocument }[0]{\AtBeginDocument }$

Phasors are essential tool in circuit analysis.

In this section, we apply the phasor transformation to an RC circuit shown in Figure 2RCcirc. To solve this circuit in the time domain, we apply Kirchoff’s voltage law, as shown in Equation eq-1 -eq0.

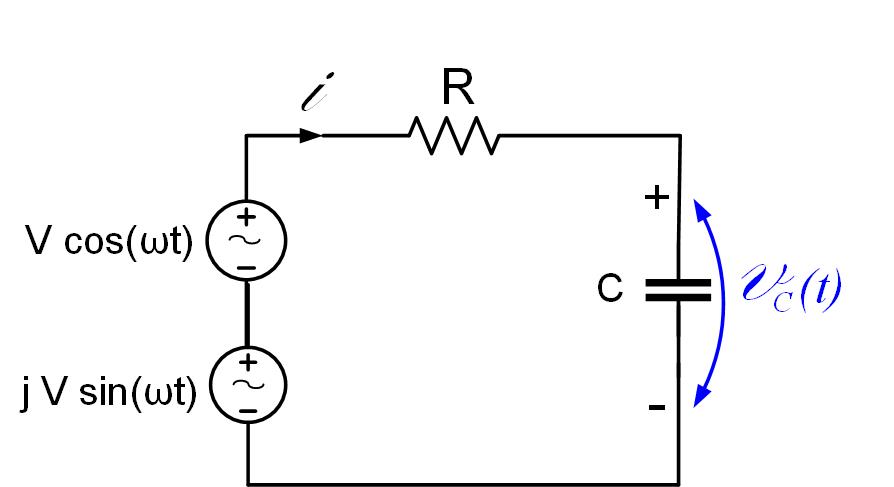
The circuit in Figure RCcirc is a simple RC circuit. Equation eq-1 shows the KVL the time domain.

$\begin{eqnarray} v_s(t)=v_R(t)+v_C(t) \label{eq-1} \\ v_s(t) = R i + \frac{1}{C} \int i(t) dt \label{eq0} \end{eqnarray}$

As we discussed in the previous section, we will be using the principle of superposition, and add another generator to the circuit, as shown in Figure RCcirc.

Figure 1: Using superposition to find phasors of voltages and currents in an RC circuit.

The generator we originally had in the circuit is now just the real part of the phasor expression shown in Equation eq2.

$\begin{eqnarray} v_s(t)= V \cos (\omega t + \Theta_V)=\Re\{ V cos (\omega t + \Theta ) + j V sin (\omega t + \Theta)\}= \nonumber \\ = \Re\{V e^{j(\omega t + \Theta)}\}=\Re\{V e^{j \Theta} e^{j \omega t}\} \label{eq2} \end{eqnarray}$

We can now use the analysis from the previous section to replace the time-domain quantities in equation eq0 with these newly developed expressions.

$\begin{eqnarray} v_s(t)=v_R(t) + v_C(t) \\ Re\{V_s e^{j \Theta_V} e^{j \omega t}\}= \Re\{R \, I e^{j \Theta_I} e^{j \omega t}\} + \Re\{ \frac{1}{j \omega C} I e^{j \Theta_I} e^{j \omega t} \} \end{eqnarray}$

A common term in the previous equation is $e^{j\omega t}$ , and we can now drop $Re$ , as long as we later remember to take only the real part of the expression for the voltage and current phasors to get the time domain expression. We can now write the equation as

$\begin{eqnarray} V_s e^{j \Theta_{V}} =R \, I e^{j \Theta_I} + \frac{1}{j \omega C} I e^{j \Theta_I} \\ \tilde{V}_s = R \tilde{I} + \frac{\tilde{I}}{j \omega C} \end{eqnarray}$

Since this is a linear equation, we can easily solve it:

$\begin{eqnarray} \tilde{I} = \frac{\tilde{V}_s}{ R + \frac{1}{j \omega C} } \label{pheq} \end{eqnarray}$

Converting the phasor back to the time domain

In general, if the phasor is $\tilde {V}=|V| e^{j \Theta _V}$ , to find the time-domain signal, we first multiply the phasor with $e^{j \omega t}$ term, and then take the real part of it.

$\begin{eqnarray} v(t)=\Re \{ \tilde{V} e^{j \omega t} \} \\ v(t)=\Re\{|\tilde{V}| e^{j(\omega t + \Theta_V)}\} \\ v(t)=\Re\{ |\tilde{V}| cos (\omega t + \Theta_V ) + j |\tilde{V}| sin (\omega t + \Theta_V)\} \\ v(t) = V cos (\omega t + \Theta_V ) \end{eqnarray}$

The phasor of current is $I=3 e^{j 45^o}$ . Obtain the signal in the time domain.

To obtain the time-domain signal from the phasor:

(a): multiply the phasor $\tilde {I}$ with the $e^{j\omega t}$ term,
(b): use Euler’s formula
(c): take the real part of the expression.

$\begin{eqnarray} i(t) = \Re\{ 3 e^{ j 45^o} e^{j\omega t} \} = \Re\{3 e^{j \omega t + 45^o} \} = \nonumber \\ = \Re \{ 3 \cos (\omega t + 45^o ) + j 3 \sin (\omega t + 45^o \} = 3 \cos (\omega t + 45^o ) \label{phtotd} \end{eqnarray}$

The phasor for the voltageis given as $\tilde {V}= 5 e^{ j \beta }$ . Find the expression for the phasor in the time domain.

$v(t) = 5 \cos \beta t$ $v(t) = 5 \cos (\omega t+ \beta )$ $v(t) = 5 \sin \beta t$