Impedance and admittance circles on the Smith Chart

$\newenvironment {prompt}{}{} \newcommand {\ungraded }[0]{} \newcommand {\todo }[0]{} \newcommand {\oiint }[0]{{\large \bigcirc }\kern -1.56em\iint } \newcommand {\mooculus }[0]{\textsf {\textbf {MOOC}\textnormal {\textsf {ULUS}}}} \newcommand {\npnoround }[0]{\nprounddigits {-1}} \newcommand {\npnoroundexp }[0]{\nproundexpdigits {-1}} \newcommand {\npunitcommand }[1]{\ensuremath {\mathrm {#1}}} \newcommand {\RR }[0]{\mathbb R} \newcommand {\R }[0]{\mathbb R} \newcommand {\N }[0]{\mathbb N} \newcommand {\Z }[0]{\mathbb Z} \newcommand {\sagemath }[0]{\textsf {SageMath}} \newcommand {\d }[0]{\mathop {}\!d} \newcommand {\l }[0]{\ell } \newcommand {\ddx }[0]{\frac {d}{\d x}} \newcommand {\zeroOverZero }[0]{\ensuremath {\boldsymbol {\tfrac {0}{0}}}} \newcommand {\inftyOverInfty }[0]{\ensuremath {\boldsymbol {\tfrac {\infty }{\infty }}}} \newcommand {\zeroOverInfty }[0]{\ensuremath {\boldsymbol {\tfrac {0}{\infty }}}} \newcommand {\zeroTimesInfty }[0]{\ensuremath {\small \boldsymbol {0\cdot \infty }}} \newcommand {\inftyMinusInfty }[0]{\ensuremath {\small \boldsymbol {\infty -\infty }}} \newcommand {\oneToInfty }[0]{\ensuremath {\boldsymbol {1^\infty }}} \newcommand {\zeroToZero }[0]{\ensuremath {\boldsymbol {0^0}}} \newcommand {\inftyToZero }[0]{\ensuremath {\boldsymbol {\infty ^0}}} \newcommand {\numOverZero }[0]{\ensuremath {\boldsymbol {\tfrac {\#}{0}}}} \newcommand {\dfn }[0]{\textbf } \newcommand {\unit }[0]{\mathop {}\!\mathrm } \newcommand {\eval }[1]{\bigg [ #1 \bigg ]} \newcommand {\seq }[1]{\left ( #1 \right )} \newcommand {\epsilon }[0]{\varepsilon } \newcommand {\phi }[0]{\varphi } \newcommand {\iff }[0]{\Leftrightarrow } \DeclareMathOperator {\arccot }{arccot} \DeclareMathOperator {\arcsec }{arcsec} \DeclareMathOperator {\arccsc }{arccsc} \DeclareMathOperator {\si }{Si} \DeclareMathOperator {\scal }{scal} \DeclareMathOperator {\sign }{sign} \newcommand {\arrowvec }[1]{{\overset {\rightharpoonup }{#1}}} \newcommand {\vec }[1]{{\overset {\boldsymbol {\rightharpoonup }}{\mathbf {#1}}}\hspace {0in}} \newcommand {\point }[1]{\left (#1\right )} \newcommand {\pt }[1]{\mathbf {#1}} \newcommand {\Lim }[2]{\lim _{\point {#1} \to \point {#2}}} \DeclareMathOperator {\proj }{\mathbf {proj}} \newcommand {\veci }[0]{{\boldsymbol {\hat {\imath }}}} \newcommand {\vecj }[0]{{\boldsymbol {\hat {\jmath }}}} \newcommand {\veck }[0]{{\boldsymbol {\hat {k}}}} \newcommand {\vecl }[0]{\vec {\boldsymbol {\l }}} \newcommand {\uvec }[1]{\mathbf {\hat {#1}}} \newcommand {\utan }[0]{\mathbf {\hat {t}}} \newcommand {\unormal }[0]{\mathbf {\hat {n}}} \newcommand {\ubinormal }[0]{\mathbf {\hat {b}}} \newcommand {\dotp }[0]{\bullet } \newcommand {\cross }[0]{\boldsymbol \times } \newcommand {\grad }[0]{\boldsymbol \nabla } \newcommand {\divergence }[0]{\grad \dotp } \newcommand {\curl }[0]{\grad \cross } \newcommand {\lto }[0]{\mathop {\longrightarrow \,}\limits } \newcommand {\bar }[0]{\overline } \newcommand {\surfaceColor }[0]{violet} \newcommand {\surfaceColorTwo }[0]{redyellow} \newcommand {\sliceColor }[0]{greenyellow} \newcommand {\vector }[1]{\left \langle #1\right \rangle } \newcommand {\sectionOutcomes }[0]{} \newcommand {\HyperFirstAtBeginDocument }[0]{\AtBeginDocument }$

Reflection Coefficient and Impedance

Reflection coefficient and impedance are related through Equation eq:SCDereqnreflectioncoefficient. We can find an impedance that corresponds to the reflection coefficient, Equation eq:SCDereqnimpedancerc. Every point on the Smith Chart represents one reflection coefficient $\Gamma$ and one impedance $Z_L$ .

$\begin{eqnarray} \Gamma = \frac{Z_L-Z_\circ}{Z_L+Z_\circ} \label{eq:SCDereqnreflectioncoefficient} \\ \nonumber \\ Z_L = Z_0 \frac{ 1+ \Gamma}{1- \Gamma } \label{eq:SCDereqnimpedancerc} \end{eqnarray}$

All impedances on the Smith Chart are normalized to the transmission line impedance $Z_0$ . The normalized impedance is denoted in Equation eq:SCDerNormImp with lowercase $z_L$ .

$\begin{eqnarray} z_L = \frac{Z_L}{Z_0} = \frac{ 1+ \Gamma}{1- \Gamma } \label{eq:SCDerNormImp} \end{eqnarray}$

Derivation of Impedance and Admittance Circles on the Smith Chart

Impedance and reflection coefficient are complex numbers. The normalized impedance has a real and imaginary part $z_L=r_L + j x_L$ , and the reflection coefficient can also be shown in Cartesian coordinates as $\Gamma = \Gamma _r + j \Gamma _i$ . We can now substitute these equations into Equation eq:SCDerRealImag.

$\begin{eqnarray} r_L + j x_L = \frac{ 1+\Gamma_r + j \Gamma_i}{1- (\Gamma_r + j \Gamma_i)} \label{eq:SCDerRealImag} \end{eqnarray}$

We can equate the real and imaginary parts on the left and right side of Equation eq:SCDerRealImag to get the equations of constant $r_L$ and $x_L$ .

$\begin{eqnarray} \left( \Gamma_r - \frac{r_L}{1+r_L} \right)^2 + \Gamma_i^2 =\left( \frac{1}{1+r_L} \right) ^2 \label{eq:SCDerRealCirc} \\ \left( \Gamma_r - 1 \right)^2 + \left(\Gamma_i - \frac{1}{x_L} \right)^2 =\left( \frac{1}{x_L} \right) ^2 \label{eq:SCDerImagCirc} \end{eqnarray}$

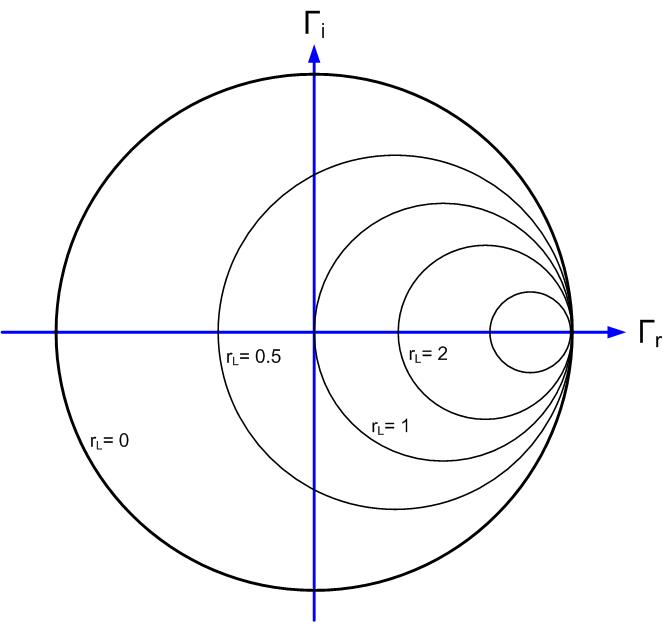
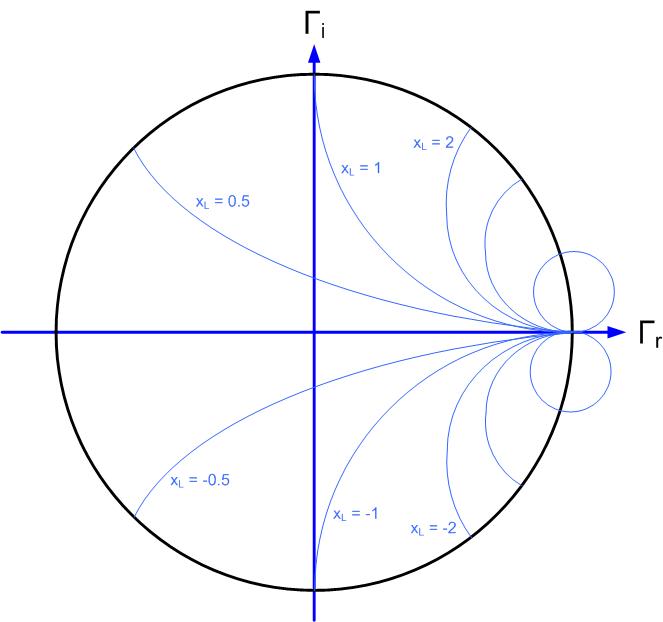
These are equations of a circle, with the constant resistance circle’s center at $(\frac {r_L}{1+r_L} ,0)$ and radius $\frac {1}{1+r_L}$ ; and the constant reactance imaginary circle center at $(1,\frac {1}{x_L})$ and radius of $\frac {1}{x_L}$ .

Figures fig:SCDerscresistance- fig:SCDerscreactance show circles on the Smith Chart that represent constant (normalized) reactances, and resistances.

Figure 1: All points on the circle have the constant real part of the impedance (resistance). Normalized resistance circles.

Figure 2: All points on the circle have the constant imaginary part of the impedance (reactance). Normalized reactance circles.

Admittance circles can be similarly derived using the fact that $Y_L=\frac {1}{Z_L}$ and the Equation eq:SCDerNormImp