- How to use the reciprocal ratios of , , and , to also obtain information about a given right triangle?
- What are the values of such reciprocal rations for the standard angles of , and ?
Introduction
Briefly speaking, we have met three fundamental ratios between sides of a right triangle: sine, cosine, and tangent. But their reciprocals are also relevant ratios between the sides of the given triangle. Now, while such reciprocal ratios turn out to carry the same information as sine, cosine, and tangent, it is useful to know how to manipulate them as well. Later, when we study trigonometric functions as actual functions of a real parameter, discussing their graphs, symmetries, etc., more differences will become apparent.
Definitions and examples
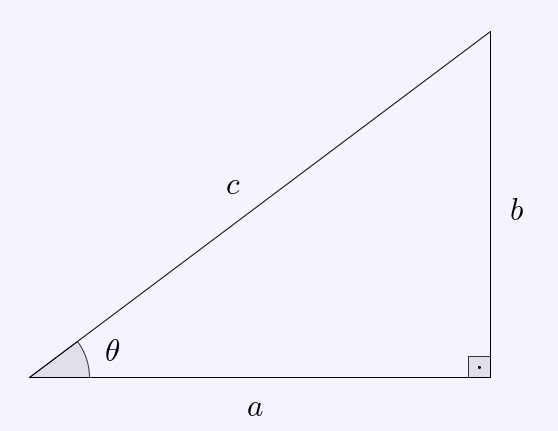
We define the secant, cosecant, and cotangent of , by
- ;
- , and;
- .
Note that since for acute angles we always have and between and , the reciprocals and will always be bigger than .
- a.
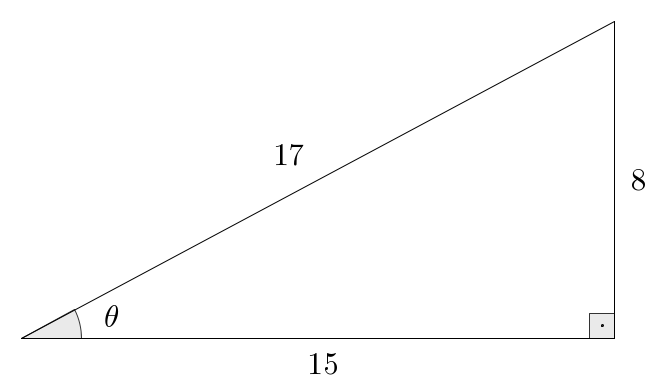
- b.
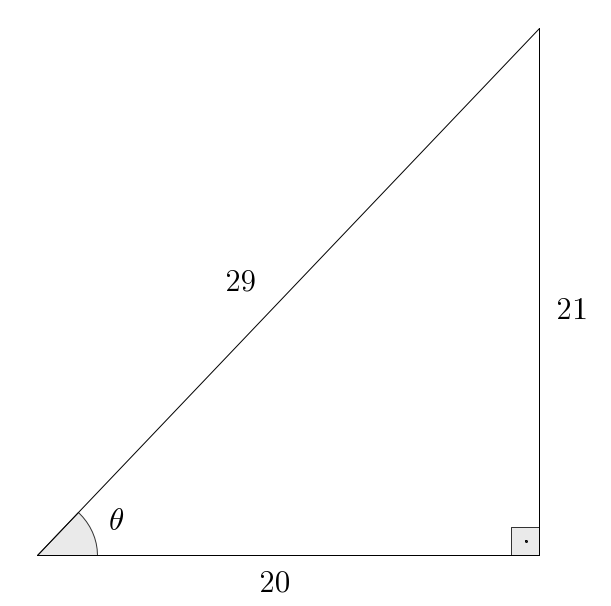
Next, we had the fundamental identity . It turns out that with this, we may obtain two extra useful identities.
You should not think of those two extra identities as something more to be memorized. The only identity worth the trouble is . The following strategy is something you can quickly reproduce on a scrap of paper if you need to recall these formulas, once you have understood the idea once:
- Divide both sides of by :
- Divide both sides of by :
- a.
- Given: on
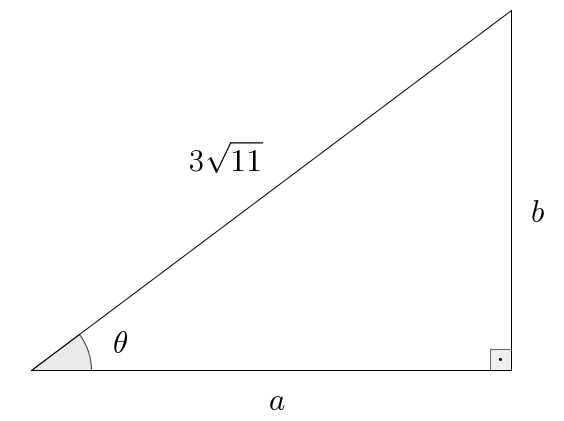
- b.
- Given: on
Values of trig functions for standard angles – bis
Previously, we have obtained the following table of standard values for sine, cosine, and tangent:
By simply inverting all of those values, we naturally obtain a similar table with standard values for secant, cosecant and cotangent. Of course, this is not another table you have to memorize, but we’ll list it here for completeness:
Note the undefined “extreme” values: is undefined, because that would be , but and we cannot divide by zero. Similarly for the other ones.
- We have defined secant, cosecant, and cotangent, as the reciprocal ratios of cosine, sine, and tangent. For each angle , we have the associated fundamental identities and , which can be easily deduced from the good old . Again, such identities can be used together with the Pythagorean Theorem to obtain information about sides of a right triangle.
- We have summarized (again in a table) the standard values of secant, cosecant, and cotangent, for the most frequent angles of , , and .