- How can we find solutions to inequalities without using a graph?
- How can we use the zeros of functions to solve inequalities?
Introduction and the Importance of Zeros
In the previous section, we constructed the following graph to solve the inequality , where .
We can see that the graph of dips below the -axis between its two -intercepts. The zeros of are and in this case and they divide the domain (the -axis) into three intervals: , and . For every number in , the graph of is above the -axis; in other words, for all in . Similarly, for all in , and for all in . We can schematically represent this with the sign diagram below.
Here, the above a portion of the number line indicates for those values of ; the indicates there. The numbers labeled on the number line are the zeros of , so we place above them. We see at once that the solution to is . Adding in the zeros, the solution to is .
Our next goal is to establish a procedure by which we can generate the sign diagram without graphing the function.
Continuity and the Intermediate Value Theorem
An important property of quadratic functions is that if the function is positive at one point and negative at another, the function must have at least one zero in between. Graphically, this means that a parabola can’t be above the -axis at one point and below the -axis at another point without crossing the -axis.
This is a special case of a theorem called the Intermediate Value Theorem, or IVT for short. To talk about the IVT, we first need to discuss what it means for a function to be continuous.
In further courses, you will learn a more formal definition of continuity, but for now, this will suffice.
- (a)
- Linear and quadratic functions are continuous.
- (b)
- In fact, all of our famous functions are continuous where they are defined.
- (c)
- All polynomials are continuous.
- (d)
- Rational functions are continuous where they are defined. In particular, is continuous on its domain, .
- (e)
- If and are continuous functions, so are and .
One way to think about continuous functions is that they are the functions whose graphs you could draw on an infinite piece of paper without ever taking your pencil off the paper (except where they aren’t defined). You will encounter and learn about continuous functions more in-depth in calculus, but for now, familiarity at this level will be enough.
Now that we know about continuous functions, we can state our version of the IVT.
Reinterpreted, this means that the graph of a continuous function can’t be above the -axis at one point and below the -axis at another point without crossing the -axis.
Here’s how we’ll use the IVT to solve inequalities of the form , where is a continuous function. If a given interval does not contain a zero of , then by the IVT either all the function values on the interval are positive or they’re all negative. In this way, the IVT allows us to determine the sign of all of the function values on the interval by testing the function at just one value in the interval, which we’re free to choose.
This gives us the following steps for solving an inequality involving a continuous function.
- (a)
- Rewrite the inequality, if necessary, as a continuous function on one side of the inequality and on the other.
- (b)
- Find the zeros of and place them on the number line with the number above them.
- (c)
- Choose a real number, called a test value, in each of the intervals determined in step 2.
- (d)
- Determine the sign of for each test value in step c, and write that sign above the corresponding interval.
- (e)
- Choose the intervals which correspond to the correct sign to solve the inequality.
As you can see, the zeros of continuous functions are important, so in the examples that follow, we’ll highlight the techniques we use to find zeros. It may also be useful to review methods for finding zeros that you’ve seen before.
Solving Inequalities Algebraically
First, we find the zeros of , where . We could do this by using the quadratic formula, but let’s factor. Factoring gives us . In order for to be true, we need or . This tells us that the zeros of are and . This gives us a good start to our sign diagram:
This sign diagram tells us that we have to check three intervals: , , and . However, thanks to the IVT, we only need to check one test value per interval. Be careful not to choose or as your test values since they are zeros.
For the interval , we choose to be our test value and see that , which is positive.
For the interval , we choose to be our test value and see that , which is negative.
For the interval , we choose to be our test value and see that , which is positive.
We can now update our sign diagram to the following:
Since we wanted to find where was negative, we choose as the solution to the inequality.
First, we find the zeros of . We start by noticing that each term in contains a factor of , so we can factor that out and find . In order to solve the equation , we need to solve and . The first equation is already solved, and tells us that is one zero of . To solve the second equation, we calculate
and note that the exponential function is never negative, so there are no solutions. Therefore, the only zero of is . We now begin to construct the sign diagram.This sign diagram tells us that we have to check two intervals: and . Again, thanks to the IVT, we only need to check one test value per interval.
For the interval , we choose to be our test value and see that , which is negative. To see that is negative, notice that , and since , . Therefore, when we subtract 1 from , we obtain a negative number.
For the interval , we choose to be our test value and see that , which is positive.
We can now update our sign diagram to the following:
Since we wanted to find where was non-negative, we choose as the solution to the inequality. Remember to include 0 in the interval, since zeros of are also points where is non-negative.
For the interval , we choose to be our test value. We see that , so is positive on the interval.
For the interval , we choose to be our test value. We see that , so is negative on the interval.
For the interval , we choose to be our test value. We see that , so is positive on the interval.
We can now construct a sign diagram.
From the sign diagram, we see on , which corresponds to where the graph of is on or above the -axis.
Dealing with Difficult Denominators
Even after we feel comfortable with the procedure for solving inequalities involving continuous functions, you might still wonder about functions which aren’t defined on all real numbers, such as rational functions or more generally, functions with denominators that could potentially evaluate to 0. The good news is that if and are continuous functions, the function is continuous wherever it is defined. Therefore, we can adapt our technique from before, but remembering that a change of sign could happen around a point where a function is undefined, so we need to add any places our functions are undefined to our sign diagram.
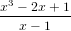 ≥
≥ x − 1
x3 − 2x + 1
__________
x − 1 − 1
2x + 1 ≥ 0
2(
x3 − 2x + 1)
− x(x − 1) + 1(2(x − 1))
_________________________________
2(x − 1) ≥ 0get a common denominator
2x3 − x2 − x
___________
2x − 2 ≥ 0expand
x − 1
x3 − 2x + 1
__________
x − 1 − 1
2x + 1 ≥ 0
2(
x3 − 2x + 1)
− x(x − 1) + 1(2(x − 1))
_________________________________
2(x − 1) ≥ 0get a common denominator
2x3 − x2 − x
___________
2x − 2 ≥ 0expand
Choosing test values in each test interval (we encourage you to check the calculation), we can construct the sign diagram below.
We used an X to denote that is not defined at .
We are interested in where . We find is positive on the intervals , and . We add to these intervals the zeros of , , and , to get our final solution: .
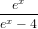 ≤ 3
ex
__
ex − 4 − 3 ≤ 0
ex
__
ex − 4 − 3(ex − 4)
ex − 4 ≤ 0Common denomintors.
12 − 2ex
ex − 4 ≤ 0
≤ 3
ex
__
ex − 4 − 3 ≤ 0
ex
__
ex − 4 − 3(ex − 4)
ex − 4 ≤ 0Common denomintors.
12 − 2ex
ex − 4 ≤ 0
We set . We note that is undefined when its denominator , or when . Solving this by taking logarithms gives , so the domain of is . To find the zeros of , we set the numerator equal to zero and obtain . Solving for , we find , or . When we build our sign diagram, finding test values may be a little tricky since we need to check values around and . Recall that the function is increasing1 which means . This indicates that we might want to use , , and as our test values. While the prospect of determining the sign of may be very unsettling, remember that , so We determine the signs of and similarly and construct the sign diagram.
From the sign diagram, we find our answer to be .
Conclusion
We hope that the specific examples we’ve gone through illustrate a general principle when it comes to solving inequalities. First, we want to rewrite the inequality in a form where 0 is on one side and a nice-enough function is on the other side. Then, we use the fact that our functions are continuous on their domains to narrow down where possible sign changes can occur. From there, we can use test values to compute the sign of the function on intervals, and finish by putting our solution in interval notation.