Domains and Ranges of Composite Functions

$\newenvironment {prompt}{}{} \newcommand {\ungraded }[0]{} \newcommand {\mooculus }[0]{\textsf {\textbf {MOOC}\textnormal {\textsf {ULUS}}}} \newcommand {\av }[0]{\mathrm {AROC}} \newcommand {\tech }[0]{Desmos} \newcommand {\calcHW }[0]{\includegraphics [width=0.5cm,trim={0 4mm 0 0}]{calc.png} \,} \newcommand {\callout }[0]{\begin {remark}} \newcommand {\overview }[0]{\begin {remark}\textbf {Overview}~} \newcommand {\objectives }[0]{\begin {remark}\textbf {Objectives}\\} \newcommand {\motivatingQuestions }[0]{\begin {remark}\textbf {Motivating Questions}~} \newcommand {\MM }[0]{\begin {remark}\textbf {Metacognitive Moment}~} \newcommand {\licenseAcknowledgement }[0]{Licensed under Creative Commons 4.0} \newcommand {\licenseAPC }[0]{\renewcommand {\licenseAcknowledgement }{\textbf {Acknowledgements:} Active Prelude to Calculus (https://activecalculus.org/prelude) }} \newcommand {\licenseSZ }[0]{\renewcommand {\licenseAcknowledgement }{\textbf {Acknowledgements:} Stitz Zeager Open Source Mathematics (https://www.stitz-zeager.com/) }} \newcommand {\licenseAPCSZ }[0]{\renewcommand {\licenseAcknowledgement }{\textbf {Acknowledgements:} Active Prelude to Calculus (https://activecalculus.org/prelude) and Stitz Zeager Open Source Mathematics (https://www.stitz-zeager.com/) }} \newcommand {\licenseORCCA }[0]{\renewcommand {\licenseAcknowledgement }{\textbf {Acknowledgements:} Original source material,products with readable and accessible math content,and other information freely available at pcc.edu/orcca.}} \newcommand {\licenseY }[0]{\renewcommand {\licenseAcknowledgement }{\textbf {Acknowledgements:} Yoshiwara Books (https://yoshiwarabooks.org/)}} \newcommand {\licenseOS }[0]{\renewcommand {\licenseAcknowledgement }{\textbf {Acknowledgements:} OpenStax College Algebra (https://openstax.org/details/books/college-algebra)}} \newcommand {\licenseAPCSZCSCC }[0]{\renewcommand {\licenseAcknowledgement }{\textbf {Acknowledgements:} Source material includes: Active Prelude to Calculus (https://activecalculus.org/prelude),Stitz Zeager Open Source Mathematics (https://www.stitz-zeager.com/),CSCC PreCalculus and Calculus texts (https://ximera.osu.edu/csccmathematics)}} \newcommand {\licenseAPCSZORCCA }[0]{\renewcommand {\licenseAcknowledgement }{\textbf {Acknowledgements:} Source material includes: Active Prelude to Calculus (https://activecalculus.org/prelude),Stitz Zeager Open Source Mathematics (https://www.stitz-zeager.com/),ORCCA: Original source material,products with readable and accessible math content,and other information freely available at pcc.edu/orcca.}} \newcommand {\sectionHeadStyle }[0]{\sffamily \bfseries } \newcommand {\thepart }[0]{\arabic {part}} \newcommand {\RR }[0]{\mathbb R} \newcommand {\R }[0]{\mathbb R} \newcommand {\N }[0]{\mathbb N} \newcommand {\Z }[0]{\mathbb Z} \newcommand {\sagemath }[0]{\textsf {SageMath}} \newcommand {\l }[0]{\ell } \newcommand {\ddx }[0]{\frac {d}{\d x}} \newcommand {\unit }[0]{\mathop {}\!\mathrm } \newcommand {\eval }[1]{\bigg [ #1 \bigg ]} \newcommand {\seq }[1]{\left ( #1 \right )} \newcommand {\epsilon }[0]{\varepsilon } \newcommand {\phi }[0]{\varphi } \newcommand {\iff }[0]{\Leftrightarrow } \DeclareMathOperator {\arccot }{arccot} \DeclareMathOperator {\arcsec }{arcsec} \DeclareMathOperator {\arccsc }{arccsc} \DeclareMathOperator {\sign }{sign} \newcommand {\lto }[0]{\mathop {\longrightarrow \,}\limits } \newcommand {\bar }[0]{\overline } \newcommand {\surfaceColor }[0]{violet} \newcommand {\surfaceColorTwo }[0]{redyellow} \newcommand {\sliceColor }[0]{greenyellow} \newcommand {\Pifont }[1]{\fontfamily {#1}\fontencoding {U}\fontseries {m}\fontshape {n}\selectfont } \newcommand {\Pisymbol }[2]{{\Pifont {#1}\char #2}} \newcommand {\Pilist }[2]{\begin {list}{\Pisymbol {#1}{#2}}{}} \newcommand {\ding }[0]{\Pisymbol {pzd}} \newcommand {\dinglist }[1]{\begin {Pilist}{pzd}{#1}} \newcommand {\dingautolist }[1]{\begin {Piautolist}{pzd}{#1}} \newcommand {\tdplotsinandcos }[3]{\pgfmathsetmacro {#1}{sin(#3)}\pgfmathsetmacro {#2}{cos(#3)}} \newcommand {\tdplotmult }[3]{\pgfmathsetmacro {#1}{#2*#3}} \newcommand {\tdplotdiv }[3]{\pgfmathsetmacro {#1}{#2/#3}} \newcommand {\tdplotcheckdiff }[5]{\par \par \pgfmathparse { abs(#2 -#1)<#3 } \par \ifthenelse {\equal {\pgfmathresult }{1}}{#4}{#5} } \newcommand {\tdplotsetmaincoords }[2]{\pgfmathsetmacro {\tdplotmaintheta }{#1} \pgfmathsetmacro {\tdplotmainphi }{#2} \tdplotcalctransformmainscreen \tikzset {tdplot_main_coords/.style={x={(\raarot cm,\rbarot cm)},y={(\rabrot cm,\rbbrot cm)},z={(\racrot cm,\rbcrot cm)}}}} \newcommand {\tdplotcalctransformmainscreen }[0]{\tdplotsinandcos {\sintheta }{\costheta }{\tdplotmaintheta }\tdplotsinandcos {\sinphi }{\cosphi }{\tdplotmainphi }\tdplotmult {\stsp }{\sintheta }{\sinphi }\tdplotmult {\stcp }{\sintheta }{\cosphi }\tdplotmult {\ctsp }{\costheta }{\sinphi }\tdplotmult {\ctcp }{\costheta }{\cosphi }\pgfmathsetmacro {\raarot }{\cosphi }\pgfmathsetmacro {\rabrot }{\sinphi }\pgfmathsetmacro {\racrot }{0}\pgfmathsetmacro {\rbarot }{-\ctsp }\pgfmathsetmacro {\rbbrot }{\ctcp }\pgfmathsetmacro {\rbcrot }{\sintheta }\pgfmathsetmacro {\rcarot }{\stsp }\pgfmathsetmacro {\rcbrot }{-\stcp }\pgfmathsetmacro {\rccrot }{\costheta }} \newcommand {\tdplotcalctransformrotmain }[0]{\tdplotsinandcos {\sinalpha }{\cosalpha }{\tdplotalpha } \tdplotsinandcos {\sinbeta }{\cosbeta }{\tdplotbeta } \tdplotsinandcos {\singamma }{\cosgamma }{\tdplotgamma } \tdplotmult {\sasb }{\sinalpha }{\sinbeta } \tdplotmult {\sbsg }{\sinbeta }{\singamma } \tdplotmult {\sasg }{\sinalpha }{\singamma } \tdplotmult {\sasbsg }{\sasb }{\singamma } \tdplotmult {\sacb }{\sinalpha }{\cosbeta } \tdplotmult {\sacg }{\sinalpha }{\cosgamma } \tdplotmult {\sbcg }{\sinbeta }{\cosgamma } \tdplotmult {\sacbsg }{\sacb }{\singamma } \tdplotmult {\sacbcg }{\sacb }{\cosgamma } \tdplotmult {\casb }{\cosalpha }{\sinbeta } \tdplotmult {\cacb }{\cosalpha }{\cosbeta } \tdplotmult {\cacg }{\cosalpha }{\cosgamma } \tdplotmult {\casg }{\cosalpha }{\singamma } \tdplotmult {\cacbsg }{\cacb }{\singamma } \tdplotmult {\cacbcg }{\cacb }{\cosgamma } \pgfmathsetmacro {\raaeul }{\cacbcg -\sasg } \pgfmathsetmacro {\rabeul }{-\cacbsg -\sacg } \pgfmathsetmacro {\raceul }{\casb } \pgfmathsetmacro {\rbaeul }{\sacbcg + \casg } \pgfmathsetmacro {\rbbeul }{-\sacbsg + \cacg } \pgfmathsetmacro {\rbceul }{\sasb } \pgfmathsetmacro {\rcaeul }{-\sbcg } \pgfmathsetmacro {\rcbeul }{\sbsg } \pgfmathsetmacro {\rcceul }{\cosbeta } } \newcommand {\tdplotcalctransformmainrot }[0]{\tdplotsinandcos {\sinalpha }{\cosalpha }{\tdplotalpha } \tdplotsinandcos {\sinbeta }{\cosbeta }{\tdplotbeta } \tdplotsinandcos {\singamma }{\cosgamma }{\tdplotgamma } \tdplotmult {\sasb }{\sinalpha }{\sinbeta } \tdplotmult {\sbsg }{\sinbeta }{\singamma } \tdplotmult {\sasg }{\sinalpha }{\singamma } \tdplotmult {\sasbsg }{\sasb }{\singamma } \tdplotmult {\sacb }{\sinalpha }{\cosbeta } \tdplotmult {\sacg }{\sinalpha }{\cosgamma } \tdplotmult {\sbcg }{\sinbeta }{\cosgamma } \tdplotmult {\sacbsg }{\sacb }{\singamma } \tdplotmult {\sacbcg }{\sacb }{\cosgamma } \tdplotmult {\casb }{\cosalpha }{\sinbeta } \tdplotmult {\cacb }{\cosalpha }{\cosbeta } \tdplotmult {\cacg }{\cosalpha }{\cosgamma } \tdplotmult {\casg }{\cosalpha }{\singamma } \tdplotmult {\cacbsg }{\cacb }{\singamma } \tdplotmult {\cacbcg }{\cacb }{\cosgamma } \pgfmathsetmacro {\raaeul }{\cacbcg -\sasg } \pgfmathsetmacro {\rabeul }{\sacbcg + \casg } \pgfmathsetmacro {\raceul }{-\sbcg } \pgfmathsetmacro {\rbaeul }{-\cacbsg -\sacg } \pgfmathsetmacro {\rbbeul }{-\sacbsg + \cacg } \pgfmathsetmacro {\rbceul }{\sbsg } \pgfmathsetmacro {\rcaeul }{\casb } \pgfmathsetmacro {\rcbeul }{\sasb } \pgfmathsetmacro {\rcceul }{\cosbeta } } \newcommand {\tdplottransformmainrot }[3]{\tdplotcalctransformmainrot \par \pgfmathsetmacro {\tdplotresx }{\raaeul * #1 + \rabeul * #2 + \raceul * #3} \pgfmathsetmacro {\tdplotresy }{\rbaeul * #1 + \rbbeul * #2 + \rbceul * #3} \pgfmathsetmacro {\tdplotresz }{\rcaeul * #1 + \rcbeul * #2 + \rcceul * #3} } \newcommand {\tdplottransformrotmain }[3]{\tdplotcalctransformrotmain \par \pgfmathsetmacro {\tdplotresx }{\raaeul * #1 + \rabeul * #2 + \raceul * #3} \pgfmathsetmacro {\tdplotresy }{\rbaeul * #1 + \rbbeul * #2 + \rbceul * #3} \pgfmathsetmacro {\tdplotresz }{\rcaeul * #1 + \rcbeul * #2 + \rcceul * #3} } \newcommand {\tdplottransformmainscreen }[3]{\tdplotcalctransformmainscreen \par \pgfmathsetmacro {\tdplotresx }{\raarot * #1 + \rabrot * #2 + \racrot * #3} \pgfmathsetmacro {\tdplotresy }{\rbarot * #1 + \rbbrot * #2 + \rbcrot * #3} } \newcommand {\tdplotsetrotatedcoords }[3]{\pgfmathsetmacro {\tdplotalpha }{#1} \pgfmathsetmacro {\tdplotbeta }{#2} \pgfmathsetmacro {\tdplotgamma }{#3} \tdplotcalctransformrotmain \par \tdplotmult {\raaeaa }{\raarot }{\raaeul } \tdplotmult {\rabeba }{\rabrot }{\rbaeul } \tdplotmult {\raceca }{\racrot }{\rcaeul } \tdplotmult {\raaeab }{\raarot }{\rabeul } \tdplotmult {\rabebb }{\rabrot }{\rbbeul } \tdplotmult {\racecb }{\racrot }{\rcbeul } \tdplotmult {\raaeac }{\raarot }{\raceul } \tdplotmult {\rabebc }{\rabrot }{\rbceul } \tdplotmult {\racecc }{\racrot }{\rcceul } \tdplotmult {\rbaeaa }{\rbarot }{\raaeul } \tdplotmult {\rbbeba }{\rbbrot }{\rbaeul } \tdplotmult {\rbceca }{\rbcrot }{\rcaeul } \tdplotmult {\rbaeab }{\rbarot }{\rabeul } \tdplotmult {\rbbebb }{\rbbrot }{\rbbeul } \tdplotmult {\rbcecb }{\rbcrot }{\rcbeul } \tdplotmult {\rbaeac }{\rbarot }{\raceul } \tdplotmult {\rbbebc }{\rbbrot }{\rbceul } \tdplotmult {\rbcecc }{\rbcrot }{\rcceul } \pgfmathsetmacro {\raarc }{\raaeaa + \rabeba + \raceca } \pgfmathsetmacro {\rabrc }{\raaeab + \rabebb + \racecb } \pgfmathsetmacro {\racrc }{\raaeac + \rabebc + \racecc } \pgfmathsetmacro {\rbarc }{\rbaeaa + \rbbeba + \rbceca } \pgfmathsetmacro {\rbbrc }{\rbaeab + \rbbebb + \rbcecb } \pgfmathsetmacro {\rbcrc }{\rbaeac + \rbbebc + \rbcecc } \tikzset {tdplot_rotated_coords/.append style={x={(\raarc cm,\rbarc cm)},y={(\rabrc cm,\rbbrc cm)},z={(\racrc cm,\rbcrc cm)}}}} \newcommand {\tdplotsetrotatedcoordsorigin }[1]{\tikzset {tdplot_rotated_coords/.append style={shift=#1}}} \newcommand {\tdplotresetrotatedcoordsorigin }[0]{\tikzset {tdplot_rotated_coords/.append style={shift={(0,0,0)}}}} \newcommand {\tdplotsetthetaplanecoords }[1]{\tdplotresetrotatedcoordsorigin \tdplotsetrotatedcoords {270 + #1}{270}{0}} \newcommand {\tdplotsetrotatedthetaplanecoords }[1]{\tdplotsetrotatedcoords {\tdplotalpha }{\tdplotbeta }{\tdplotgamma + #1}\tikzset {tdplot_rotated_coords/.append style={y={(\raarc cm,\rbarc cm)},z={(\rabrc cm,\rbbrc cm)},x={(\racrc cm,\rbcrc cm)}}}} \newcommand {\tdplotsetcoord }[4]{\tdplotsinandcos {\sinthetavec }{\costhetavec }{#3}\tdplotsinandcos {\sinphivec }{\cosphivec }{#4}\tdplotmult {\stcpv }{\sinthetavec }{\cosphivec }\tdplotmult {\stspv }{\sinthetavec }{\sinphivec }\coordinate (#1) at ($#2*(\stcpv ,\stspv ,\costhetavec )$); \coordinate (#1xy) at ($#2*(\stcpv ,\stspv ,0)$); \coordinate (#1xz) at ($#2*(\stcpv ,0,\costhetavec )$); \coordinate (#1yz) at ($#2*(0,\stspv ,\costhetavec )$); \coordinate (#1x) at ($#2*(\stcpv ,0,0)$); \coordinate (#1y) at ($#2*(0,\stspv ,0)$); \coordinate (#1z) at ($#2*(0,0,\costhetavec )$); } \newcommand {\tdplotsimplesetcoord }[4]{\tdplotsinandcos {\sinthetavec }{\costhetavec }{#3}\tdplotsinandcos {\sinphivec }{\cosphivec }{#4}\tdplotmult {\stcpv }{\sinthetavec }{\cosphivec }\tdplotmult {\stspv }{\sinthetavec }{\sinphivec }\coordinate (#1) at ($#2*(\stcpv ,\stspv ,\costhetavec )$); } \newcommand {\tdplotsetpolarplotrange }[4]{\pgfmathsetmacro {\tdplotlowerphi }{#3} \pgfmathsetmacro {\tdplotupperphi }{#4} \pgfmathsetmacro {\tdplotlowertheta }{#1} \pgfmathsetmacro {\tdplotuppertheta }{#2} } \newcommand {\tdplotresetpolarplotrange }[0]{\pgfmathsetmacro {\tdplotlowerphi }{0} \pgfmathsetmacro {\tdplotupperphi }{360} \pgfmathsetmacro {\tdplotlowertheta }{0} \pgfmathsetmacro {\tdplotuppertheta }{180} } \newcommand {\tdplotdosurfaceplot }[6]{\par \pgfmathsetmacro {\nextphi }{\curphi + \tdplotsuperfudge *\viewphistep } \par \begin {scope}[opacity=1] \par \par \tdplotcheckdiff {\nextphi }{360}{\origviewphistep }{#2}{} \tdplotcheckdiff {\nextphi }{0}{\origviewphistep }{#2}{} \par \tdplotcheckdiff {\nextphi }{90}{\origviewphistep }{#3}{} \tdplotcheckdiff {\nextphi }{450}{\origviewphistep }{#3}{} \end {scope} \par \foreach \curtheta in{\viewthetastart ,\viewthetainc ,...,\viewthetaend } { \par \pgfmathsetmacro {\curlongitude }{90 -\curphi } \pgfmathsetmacro {\curlatitude }{90 -\curtheta } \par \ifthenelse {\equal {\leftright }{-1.0}}{\pgfmathsetmacro {\curphi }{\curphi -\origviewphistep } }{} \par \pgfmathsetmacro {\tdplottheta }{mod(\curtheta ,360)} \pgfmathsetmacro {\tdplotphi }{mod(\curphi ,360)} \par \pgfmathparse {\tdplotphi <0} \ifthenelse {\equal {\pgfmathresult }{1}}{ \pgfmathsetmacro {\tdplotphi }{\tdplotphi + 360} }{}\par \pgfmathparse {\tdplottheta >\tdplotuppertheta } \pgfmathsetmacro {\logictest }{1 -\pgfmathresult } \par \pgfmathparse {\tdplottheta <\tdplotlowertheta } \pgfmathsetmacro {\logictest }{\logictest * (1 -\pgfmathresult )} \par \pgfmathsetmacro {\tdplottheta }{\tdplottheta + \viewthetastep } \pgfmathparse {\tdplottheta >\tdplotuppertheta } \pgfmathsetmacro {\logictest }{\logictest * (1 -\pgfmathresult )} \par \pgfmathparse {\tdplottheta <\tdplotlowertheta } \pgfmathsetmacro {\logictest }{\logictest * (1 -\pgfmathresult )} \par \pgfmathparse {\tdplotphi >\tdplotupperphi } \pgfmathsetmacro {\logictest }{\logictest * (1 -\pgfmathresult )} \par \pgfmathparse {\tdplotphi <\tdplotlowerphi } \pgfmathsetmacro {\logictest }{\logictest * (1 -\pgfmathresult )} \par \pgfmathsetmacro {\tdplotphi }{\tdplotphi + \viewphistep } \par \pgfmathparse {\tdplotphi <0} \ifthenelse {\equal {\pgfmathresult }{1}}{ \pgfmathsetmacro {\tdplotphi }{\tdplotphi + 360} }{}\par \pgfmathparse {\tdplotphi >\tdplotupperphi } \pgfmathsetmacro {\logictest }{\logictest * (1 -\pgfmathresult )} \par \pgfmathparse {\tdplotphi <\tdplotlowerphi } \pgfmathsetmacro {\logictest }{\logictest * (1 -\pgfmathresult )} \par \par \pgfmathsetmacro {\tdplottheta }{\curtheta } \pgfmathsetmacro {\tdplotphi }{\curphi } \par \ifthenelse {\equal {#6}{parametricfill}}{\ifthenelse {\equal {\logictest }{1.0}}{\pgfmathsetmacro {\radius }{#1} \pgfmathsetmacro {\tdplotr }{\radius *360} \par \pgfmathlessthan {\radius }{0} \pgfmathsetmacro {\phaseshift }{180 * \pgfmathresult } \par \pgfmathsetmacro {\colorarg }{#5} \pgfmathsetmacro {\colorarg }{\colorarg + \phaseshift } \pgfmathsetmacro {\colorarg }{mod(\colorarg ,360)} \par \pgfmathlessthan {\colorarg }{0} \pgfmathsetmacro {\colorarg }{\colorarg + 360*\pgfmathresult } \par \pgfmathdivide {\colorarg }{360} \definecolor {tdplotfillcolor}{hsb}{\pgfmathresult ,1,1} \color {tdplotfillcolor} }{}}{\pgfsetfillcolor {#5} } \pgfsetstrokecolor {#4} \par \ifthenelse {\equal {\leftright }{-1.0}}{\pgfmathsetmacro {\curphi }{\curphi + \origviewphistep } }{} \par \ifthenelse {\equal {\logictest }{1.0}}{\pgfmathsetmacro {\radius }{abs(#1)} \pgfpathmoveto {\pgfpointspherical {\curlongitude }{\curlatitude }{\radius }} \par \pgfmathsetmacro {\tdplotphi }{\curphi + \viewphistep } \pgfmathsetmacro {\radius }{abs(#1)} \pgfpathlineto {\pgfpointspherical {\curlongitude -\viewphistep }{\curlatitude }{\radius }} \par \pgfmathsetmacro {\tdplottheta }{\curtheta + \viewthetastep } \pgfmathsetmacro {\radius }{abs(#1)} \pgfpathlineto {\pgfpointspherical {\curlongitude -\viewphistep }{\curlatitude -\viewthetastep }{\radius }} \par \pgfmathsetmacro {\tdplotphi }{\curphi } \pgfmathsetmacro {\radius }{abs(#1)} \pgfpathlineto {\pgfpointspherical {\curlongitude }{\curlatitude -\viewthetastep }{\radius }} \pgfpathclose \par \pgfusepath {fill,stroke} }{} } } \newcommand {\tdplotshowargcolorguide }[4]{ \par \pgfmathsetmacro {\tdplotx }{#1} \pgfmathsetmacro {\tdploty }{#2} \pgfmathsetmacro {\tdplothuestep }{5} \pgfmathsetmacro {\tdplotxsize }{#3} \pgfmathsetmacro {\tdplotysize }{#4} \par \pgfmathsetmacro {\tdplotyscale }{\tdplotysize /360} \par \foreach \tdplotphi in {0,\tdplothuestep ,...,360} { \pgfmathdivide {\tdplotphi }{360} \definecolor {tdplotfillcolor}{hsb}{\pgfmathresult ,1,1} \color {tdplotfillcolor} \par \pgfmathsetmacro {\tdplotstarty }{\tdploty + \tdplotphi * \tdplotyscale } \pgfmathsetmacro {\tdplotstopy }{\tdplotstarty + \tdplothuestep * \tdplotyscale } \pgfmathsetmacro {\tdplotstartx }{\tdplotx } \pgfmathsetmacro {\tdplotstopx }{\tdplotx + \tdplotxsize } \filldraw [tdplot_screen_coords] (\tdplotstartx ,\tdplotstarty ) rectangle (\tdplotstopx ,\tdplotstopy ); } \par \pgfmathsetmacro {\tdplotstopy }{\tdploty + (360+\tdplothuestep )*\tdplotyscale } \pgfmathsetmacro {\tdplotstopx }{\tdplotx + \tdplotxsize } \par \draw [tdplot_screen_coords] (\tdplotx ,\tdploty ) rectangle (\tdplotstopx ,\tdplotstopy ); \par \node [tdplot_screen_coords,anchor=west,xshift=5pt] at (\tdplotstopx ,\tdploty ) {$0$}; \node [tdplot_screen_coords,anchor=west,xshift=5pt] at (\tdplotstopx ,\tdplotstopy ) {$2\pi $}; \par \pgfmathsetmacro {\tdplotstopy }{\tdploty + (360+\tdplothuestep )/2*\tdplotyscale } \node [tdplot_screen_coords,anchor=west,xshift=5pt] at (\tdplotstopx ,\tdplotstopy ) {$\pi $}; } \newcommand {\tdplotgetpolarcoords }[3]{\pgfmathsetmacro {\vxcalc }{#1} \pgfmathsetmacro {\vycalc }{#2} \pgfmathsetmacro {\vzcalc }{#3} \pgfmathsetmacro {\vcalc }{ sqrt((\vxcalc )^2 + (\vycalc )^2 + (\vzcalc )^2) } \par \pgfmathsetmacro {\vxycalc }{ sqrt((\vxcalc )^2 + (\vycalc )^2) } \par \pgfmathsetmacro {\tdplotrestheta }{asin(\vxycalc /\vcalc )} \pgfmathparse {\vzcalc <0} \ifthenelse {\equal {\pgfmathresult }{1}}{\pgfmathsetmacro {\tdplotrestheta }{180 -\tdplotrestheta } } {} \ifthenelse {\equal {\vxcalc }{0.0}}{\pgfmathparse {\vycalc <0} \ifthenelse {\equal {\pgfmathresult }{1}}{\pgfmathsetmacro {\tdplotresphi }{270} } {\pgfmathparse {\vycalc >0} \ifthenelse {\equal {\pgfmathresult }{1}}{\pgfmathsetmacro {\tdplotresphi }{90} } {\pgfmathsetmacro {\tdplotresphi }{0} } } } {\pgfmathsetmacro {\tdplotresphi }{atan(\vycalc /\vxcalc )} \pgfmathparse {\vxcalc <0} \ifthenelse {\equal {\pgfmathresult }{1}}{\pgfmathsetmacro {\tdplotresphi }{\tdplotresphi +180} } { } \par \pgfmathparse {\tdplotresphi <0} \ifthenelse {\equal {\pgfmathresult }{1}}{\pgfmathsetmacro {\tdplotresphi }{\tdplotresphi +360} } {} } } \newcommand {\npnoround }[0]{\nprounddigits {-1}} \newcommand {\npnoroundexp }[0]{\nproundexpdigits {-1}} \newcommand {\npunitcommand }[1]{\ensuremath {\mathrm {#1}}} \newcommand {\drawnestedsets }[4]{ \def \position {#1} \def \nbsets {#2} \def \listofnestedsets {#3} \def \reversedlistofcolors {#4} \coordinate (circle-0) at (#1); \coordinate (set-0) at (#1); \foreach \set [count=\c ] in \listofnestedsets { \pgfmathtruncatemacro {\cminusone }{\c -1} \node [below=3pt of circle-\cminusone ,inner sep=0] (set-\c ) {\set }; \node [circle,inner sep=0,fit=(circle-\cminusone )(set-\c )] (circle-\c ) {}; } \begin {scope}[on background layer] \foreach \col [count=\c ] in \reversedlistofcolors { \pgfmathtruncatemacro {\invc }{\nbsets -\c } \pgfmathtruncatemacro {\invcplusone }{\invc +1} \node [circle,draw,fill=\col ,inner sep=0,fit=(circle-\invc )(set-\invcplusone )] {}; } \end {scope} } \newcommand {\abs }[1]{\left \lvert #1\right \rvert } \newcommand {\highlight }[1]{\definecolor {sapphire}{RGB}{59,90,125} {\color {sapphire}{{#1}}}} \newcommand {\firsthighlight }[1]{\definecolor {sapphire}{RGB}{59,90,125} {\color {sapphire}{{#1}}}} \newcommand {\secondhighlight }[1]{\definecolor {emerald}{RGB}{20,97,75} {\color {emerald}{{#1}}}} \newcommand {\unhighlight }[1]{{\color {black}{{#1}}}} \newcommand {\lowlight }[1]{{\color {lightgray}{#1}}} \newcommand {\attention }[1]{\mathord {\overset {\downarrow }{#1}}} \newcommand {\nextoperation }[1]{\mathord {\boxed {#1}}} \newcommand {\substitute }[1]{{\color {blue}{{#1}}}} \newcommand {\pinover }[2]{\overset {\overset {\mathrm {\ #2\ }}{|}}{\strut #1 \strut }} \newcommand {\addright }[1]{{\color {blue}{{{}+#1}}}} \newcommand {\addleft }[1]{{\color {blue}{{#1+{}}}}} \newcommand {\subtractright }[1]{{\color {blue}{{{}-#1}}}} \newcommand {\divideunder }[2]{\frac {#1}{{\color {blue}{{#2}}}}} \newcommand {\divideright }[1]{{\color {blue}{{{}\div #1}}}} \newcommand {\negate }[1]{{\color {blue}{{-}}}\left (#1\right )} \newcommand {\cancelhighlight }[1]{\definecolor {sapphire}{RGB}{59,90,125}{\color {sapphire}{{\cancel {#1}}}}} \newcommand {\secondcancelhighlight }[1]{\definecolor {emerald}{RGB}{20,97,75}{\color {emerald}{{\bcancel {#1}}}}} \newcommand {\thirdcancelhighlight }[1]{\definecolor {amethyst}{HTML}{70485b}{\color {amethyst}{{\xcancel {#1}}}}} \newcommand {\lt }[0]{<} \newcommand {\gt }[0]{>} \newcommand {\amp }[0]{&} \newcommand {\apple }[0]{PICTURE OF APPLE} \newcommand {\banana }[0]{PICTURE OF BANANA} \newcommand {\pear }[0]{PICTURE OF PEAR} \newcommand {\cat }[0]{PICTURE OF CAT} \newcommand {\dog }[0]{PICTURE OF DOG} \newcommand {\dfn }[1]{\textbf {#1}\index {#1}} \newcommand {\newrobustcmd }[0]{} \newcommand {\csshow }[1]{\begingroup \expandafter \endgroup \expandafter \show \csname #1\endcsname } \newcommand {\csmeaning }[1]{\ifcsname #1\endcsname \expandafter \meaning \csname #1\endcsname \else \detokenize {undefined}\fi } \newcommand {\ifdefmacro }[0]{} \newcommand {\ifdefparam }[0]{} \newcommand {\ifdefprotected }[0]{} \newcommand {\ifnumequal }[1]{\ifnumcomp {#1}=} \newcommand {\ifnumgreater }[1]{\ifnumcomp {#1}>} \newcommand {\ifnumless }[1]{\ifnumcomp {#1}<} \newcommand {\ifdimequal }[1]{\ifdimcomp {#1}=} \newcommand {\ifdimgreater }[1]{\ifdimcomp {#1}>} \newcommand {\ifdimless }[1]{\ifdimcomp {#1}<} \newcommand {\expandonce }[1]{\unexpanded \expandafter {#1}} \newcommand {\csexpandonce }[1]{\expandafter \expandonce \csname #1\endcsname } \newcommand {\protecting }[0]{} \newcommand {\csdef }[1]{\expandafter \def \csname #1\endcsname } \newcommand {\csedef }[1]{\expandafter \edef \csname #1\endcsname } \newcommand {\csgdef }[1]{\expandafter \gdef \csname #1\endcsname } \newcommand {\csxdef }[1]{\expandafter \xdef \csname #1\endcsname } \newcommand {\cslet }[2]{\expandafter \let \csname #1\endcsname #2} \newcommand {\letcs }[2]{\ifcsdef {#2} {\expandafter \let \expandafter #1\csname #2\endcsname } {\undef #1}} \newcommand {\csletcs }[2]{\ifcsdef {#2} {\expandafter \let \csname #1\expandafter \endcsname \csname #2\endcsname } {\csundef {#1}}} \newcommand {\csuse }[1]{\ifcsname #1\endcsname \csname #1\expandafter \endcsname \fi } \newcommand {\appto }[2]{\ifundef {#1} {\edef #1{\unexpanded {#2}}} {\edef #1{\expandonce #1\unexpanded {#2}}}} \newcommand {\eappto }[2]{\ifundef {#1} {\edef #1{#2}} {\edef #1{\expandonce #1#2}}} \newcommand {\gappto }[2]{\ifundef {#1} {\xdef #1{\unexpanded {#2}}} {\xdef #1{\expandonce #1\unexpanded {#2}}}} \newcommand {\xappto }[2]{\ifundef {#1} {\xdef #1{#2}} {\xdef #1{\expandonce #1#2}}} \newcommand {\preto }[2]{\ifundef {#1} {\edef #1{\unexpanded {#2}}} {\edef #1{\unexpanded {#2}\expandonce #1}}} \newcommand {\epreto }[2]{\ifundef {#1} {\edef #1{#2}} {\edef #1{#2\expandonce #1}}} \newcommand {\gpreto }[2]{\ifundef {#1} {\xdef #1{\unexpanded {#2}}} {\xdef #1{\unexpanded {#2}\expandonce #1}}} \newcommand {\xpreto }[2]{\ifundef {#1} {\xdef #1{#2}} {\xdef #1{#2\expandonce #1}}} \newcommand {\csappto }[1]{\expandafter \appto \csname #1\endcsname } \newcommand {\cseappto }[1]{\expandafter \eappto \csname #1\endcsname } \newcommand {\csgappto }[1]{\expandafter \gappto \csname #1\endcsname } \newcommand {\csxappto }[1]{\expandafter \xappto \csname #1\endcsname } \newcommand {\cspreto }[1]{\expandafter \preto \csname #1\endcsname } \newcommand {\csepreto }[1]{\expandafter \epreto \csname #1\endcsname } \newcommand {\csgpreto }[1]{\expandafter \gpreto \csname #1\endcsname } \newcommand {\csxpreto }[1]{\expandafter \xpreto \csname #1\endcsname } \newcommand {\csnumdef }[1]{\expandafter \numdef \csname #1\endcsname } \newcommand {\csnumgdef }[1]{\expandafter \numgdef \csname #1\endcsname } \newcommand {\csdimdef }[1]{\expandafter \dimdef \csname #1\endcsname } \newcommand {\csdimgdef }[1]{\expandafter \dimgdef \csname #1\endcsname } \newcommand {\csgluedef }[1]{\expandafter \gluedef \csname #1\endcsname } \newcommand {\csgluegdef }[1]{\expandafter \gluegdef \csname #1\endcsname } \newcommand {\mudef }[2]{\ifundef #1{\def #1{0mu}}{}\edef #1{\the \muexpr #2}} \newcommand {\csmudef }[1]{\expandafter \mudef \csname #1\endcsname } \newcommand {\csmugdef }[1]{\expandafter \mugdef \csname #1\endcsname } \newcommand {\listbreak }[0]{} \newcommand {\listadd }[2]{\ifblank {#2}{}{\appto #1{#2|}}} \newcommand {\listgadd }[2]{\ifblank {#2}{}{\gappto #1{#2|}}} \newcommand {\listcsadd }[1]{\expandafter \listadd \csname #1\endcsname } \newcommand {\listcseadd }[1]{\expandafter \listeadd \csname #1\endcsname } \newcommand {\listcsgadd }[1]{\expandafter \listgadd \csname #1\endcsname } \newcommand {\listcsxadd }[1]{\expandafter \listxadd \csname #1\endcsname } \newcommand {\dolistloop }[0]{\forlistloop \do } \newcommand {\dolistcsloop }[0]{\forlistcsloop \do } \newcommand {\AfterPreamble }[0]{\AtBeginDocument } \newcommand {\see }[2]{\emph {\seename } #1} \newcommand {\seealso }[2]{\emph {\alsoname } #1} \newcommand {\seename }[0]{see} \newcommand {\alsoname }[0]{see also} \newcommand {\printindex }[0]{} \newcommand {\HyperFirstAtBeginDocument }[0]{\AtBeginDocument } \newcommand {\licenseAcknowledgement }[0]{\textbf {Acknowledgements:} OpenStax College Algebra (https://openstax.org/details/books/college-algebra)}$

We explore the domain and range of a composite function.

Motivating Questions

How does the process of function composition affect the domain of the function?
How does the process of function composition affect the range of the function?

Domains of Composite Functions

The domain of a composite function, such as $f \circ g$ , is dependent on the domain of $g$ and the domain of $f$ . The domain of $f \circ g$ is important because it tells us when we can apply a composite function and when we cannot.

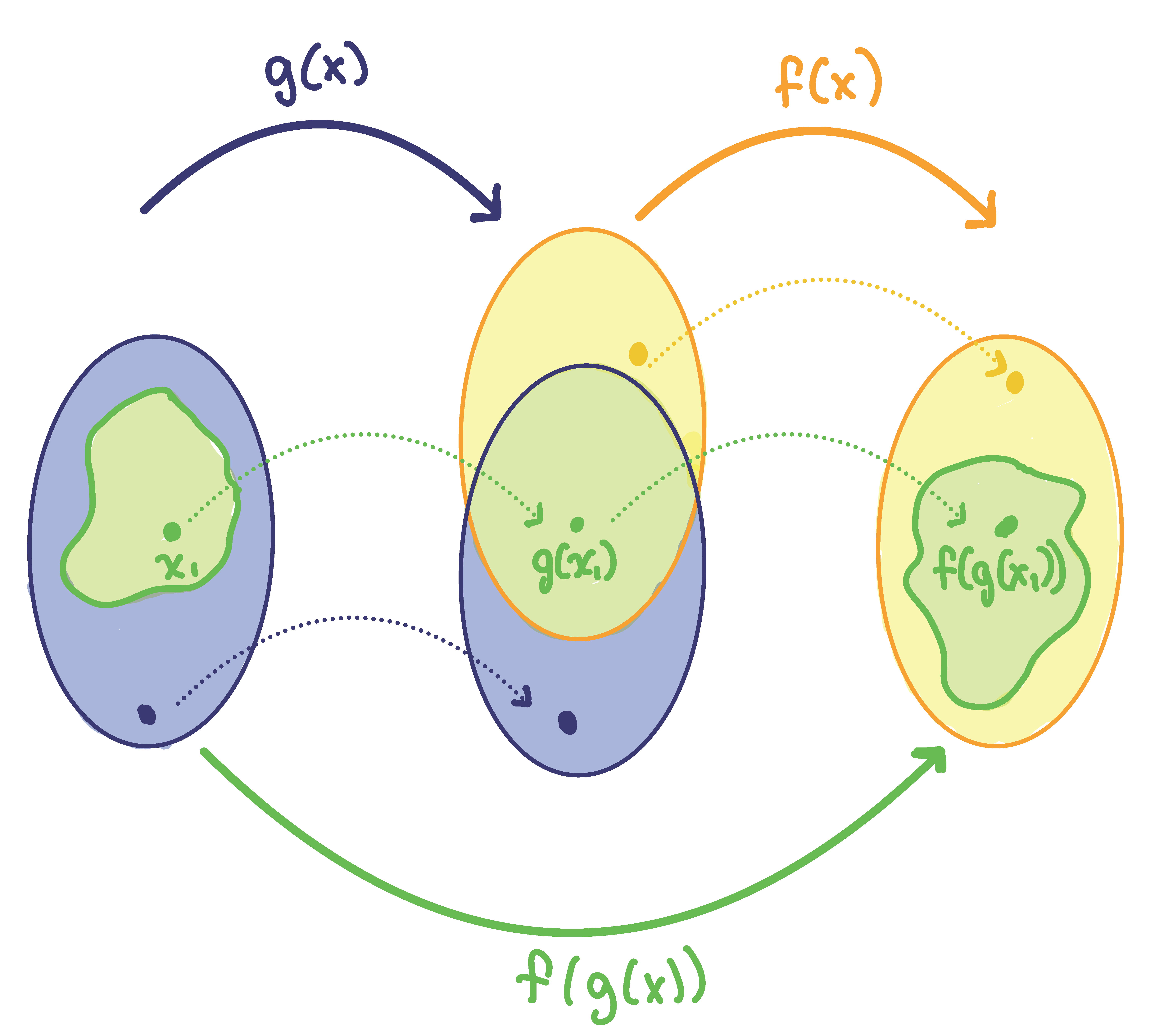
Let us assume we know the domains of the functions $f$ and $g$ separately. We can write the composite function $f \circ g$ for an input $x$ as $f(g(x))$ . Using the figure in Remark 2 below, we can see that $x$ must be a member of the domain of $g$ in order for the expression to be meaningful, because otherwise we cannot complete the inner function evaluation. However, we also see that $g(x)$ must be a member of the domain of $f$ , otherwise the second function evaluation in $f(g(x))$ cannot be completed, and the expression is still undefined. Thus the domain of $f \circ g$ consists of only those inputs in the domain of $g$ that produce outputs from $g$ belonging to the domain of $f$ . Note that the domain of $f$ composed with $g$ is the set of all $x$ such that $x$ is in the domain of $g$ and $g(x)$ is in the domain of $f$ .

The domain of a composite function $f(g(x))$ is the set of those inputs $x$ in the domain of $g$ for which $g(x)$ is in the domain of $f$ .

To find the domain of a composite function, $f\circ g$ , you can follow these three steps:

1): Find the domain of $g$ .
2): Find the domain of $f$ .
3): Find those inputs $x$ in the domain of $g$ for which $g(x)$ is in the domain of $f$ . That is, exclude those inputs $x$ from the domain of $g$ for which $g(x)$ is not in the domain of $f$ . The resulting set is the domain of $f \circ g$ .

Find the domain of $f \circ g$ where $f(x)=\frac {5}{x-1}$ and $g(x)=\frac {4}{3x-2}$ .

The domain of $g$ consists of all real numbers except $x=\frac {2}{3}$ , since that input value would cause us to divide by 0. Likewise, the domain of $f$ consists of all real numbers except $1$ . We need to exclude from the domain of $g$ any value of $x$ for which $g(x)=1$ . $\begin{align*} \frac{4}{3x-2} &=1\\ 4 &=3x-2\\ 6 &=3x\\ x &=2 \end{align*}$

So the domain of $f \circ g$ is the set of all real numbers except $\frac {2}{3}$ and $2$ . This means that

$x \neq \frac {2}{3} \text { or } x \neq 2$

We can write this in interval notation as $\left (-\infty ,\frac {2}{3}\right ) \cup \left (\frac {2}{3},2\right ) \cup \left (2,\infty \right )$

Find the domain of $f \circ g$ where $f(x)=\sqrt {x+2}$ and $g(x)=\sqrt {3-x}$ .

Because we cannot take the square root of a negative number, the domain of $g$ is $(-\infty ,3]$ . Now we check the domain of the composite function

$(f \circ g)(x)=\sqrt {\sqrt {3-x}+2}$

For $(f \circ g)(x)=\sqrt {\sqrt {3-x}+2}$ , we need $\sqrt {3-x}+2 \geq 0$ , since the inside of a square root cannot be negative. Since square roots are non-negative, $\sqrt {3-x} \geq 0$ and $\sqrt {3-x}+2 \geq 0$ as long as $\sqrt {3-x}$ exists. That means $3-x \geq 0$ , which gives a domain of $(- \infty ,3]$ .

This example shows that knowledge of the range of functions (specifically the inner function, which in this case the range is $\sqrt {3-x} \geq 0$ ) can also be helpful in finding the domain of a composite function. It also shows that the domain of $f \circ g$ can contain values that are not in the domain of $f$ , though they must be in the domain of $g$ . In this example, the domain of $f$ is $\left (-2,\infty \right )$ but the domain of $f \circ g$ is $(- \infty ,3]$ .

Find the domain of $f \circ g$ where $f(x)=\frac {1}{x-2}$ and $g(x)=\sqrt {x+4}$ .

Ranges of Composite Functions

The range of a composite function such as $f \circ g$ is dependent on the range of $g$ and the range of $f$ . It is important to know what values can result from a composite function, that is, to know the range of a function such as $f \circ g$ .

Let us assume we know the ranges of the functions $f$ and $g$ separately. If we write the composite function for an input $x$ as $f(g(x))$ , we can see that $f(g(x))$ must be a member of the range of $f$ since we will input the value $g(x)$ into $f$ . However, we also see that it is possible that not all values in the range of $f$ are in the range of $f(g(x))$ .

From the image above, we can see that there might be values in the yellow region which are in the range of $f$ but for which there are no $x$ values for which $f(g(x))$ gives that output.

The range of a composite function $f\circ g$ is a subset of the range of $f$ .

To find the range of a composite function, $f \circ g$ , you can follow these three steps:

1): Find the range of $g$ .
2): Find the range of $f$ .
3): Restrict the domain of $f$ to the range of $g$ and then determine the outputs of $f$ of these values.

Find the range of $f \circ g$ where $f(x)=\sqrt {x+2}$ and $g(x)=\sqrt {3-x}$ .

Because the output of a square root is always a positive number, the range of $g$ is $[0,\infty )$ . Similarly, the range of $f$ is $[0,\infty )$ . But now we must think about what happens when we restrict the input of $f$ to values in the range of $g$ , $[0,\infty )$ . If $x \geq 0$ , then $x+2 \geq 2$ . Taking the square root of both sides, we see that possible outputs of $f(g(x))$ will be $\sqrt {x+2} \geq \sqrt {2}$ . That is, the range of $f \circ g$ is $[\sqrt {2},\infty )$ .

If we look at this function in Desmos, we can confirm graphically that this answer makes sense. What we want to do is think about collapsing the graph unto the $y$ -axis. The range of the function will be the $y$ -values that correspond to a point $(x,y)$ on the curve.

First, we graph the function using a standard window.

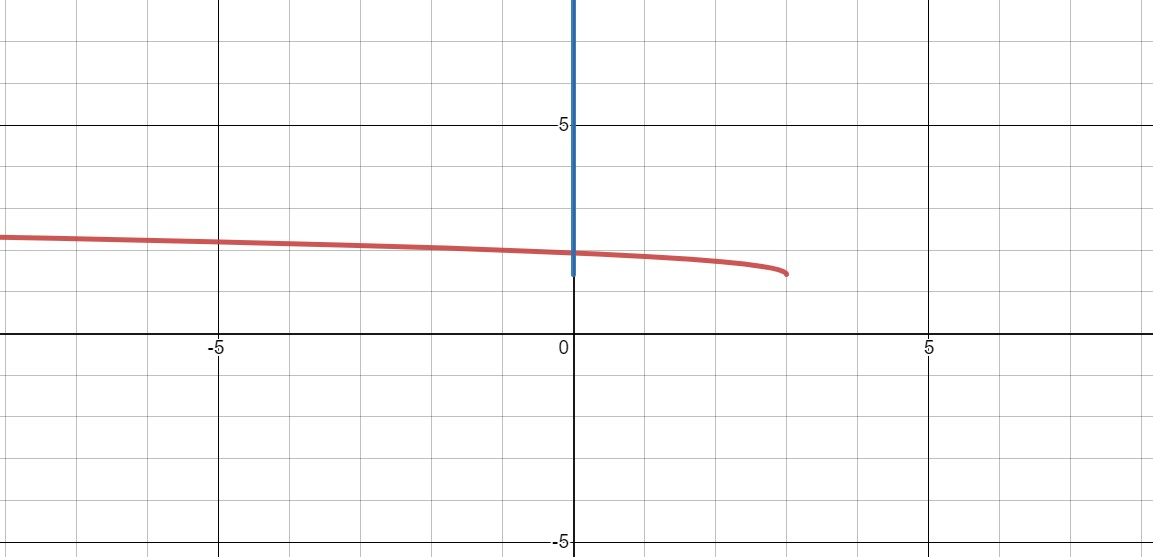
This allows us to see the domain pretty well. In the previous example, we found the domain to be $(- \infty ,3]$ and if we collapse this function to the $x$ -axis, it looks like the $x$ -values that correspond to points on this curve are exactly the $x$ in $(- \infty ,3]$ . If might be difficult to tell the domain from this graph, though. Let’s zoom out some.

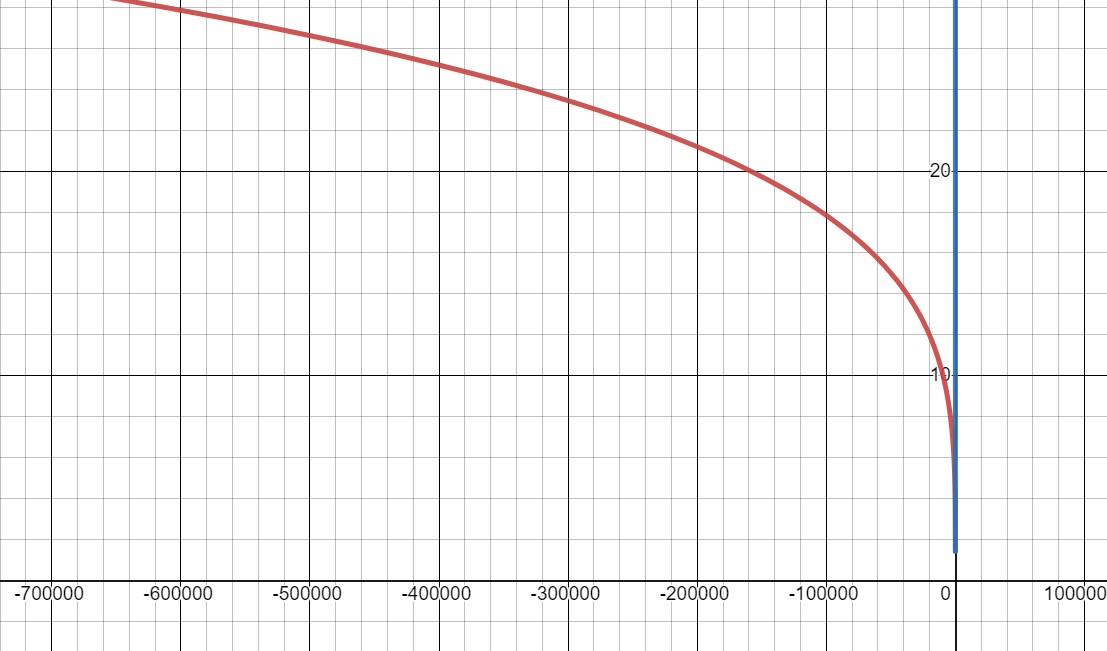
Here is the same graph in Desmos, so you can zoom in and out yourself.

This browser does not support embedded elements.

You can now see that the blue line is showing this graph collapsed to the $y$ -axis. We can tell that the range will be positive numbers above some value between 1 and 2. This corresponds with our result above of $[\sqrt {2},\infty )$ . In order to find the exact point $\sqrt {2}$ where the interval begins or to confirm that the interval really goes to infinity, we need to do the reasoning above.

For a composite function $f \circ g$ to be defined, we need outputs of $g$ to be among the allowed inputs for $f$ . In particular, if the range of $g$ is a subset of the domain of $f$ , we can say that if $g : A \to B$ and $f : B \to C$ , then $f \circ g : A \to C$ . In this case, the domain of the composite function is the domain of the inner function, and the range of the composite function is the codomain of the outer function.
In general, the domain of a composite function $f \circ g$ is the set of those inputs $x$ in the domain of $g$ for which $g(x)$ is in the domain of $f$ .
In general, the range of a composite function $f \circ g$ is a subset of the range of $f$ .