We explore what it means to find the zero of a function.
- What does it mean to find the zero of a function?
- What are other terms used for zeros of functions?
- Why might we want to find the zero of a function?
Introduction
In this section, we will study zeros of functions. Let’s start with a classic example of when we might want to find the zero of a function.
Notice that while the ball goes straight up and down, the graph of the distance from the ground vs. time makes an upside down parabola.
As the ball goes up, we see:
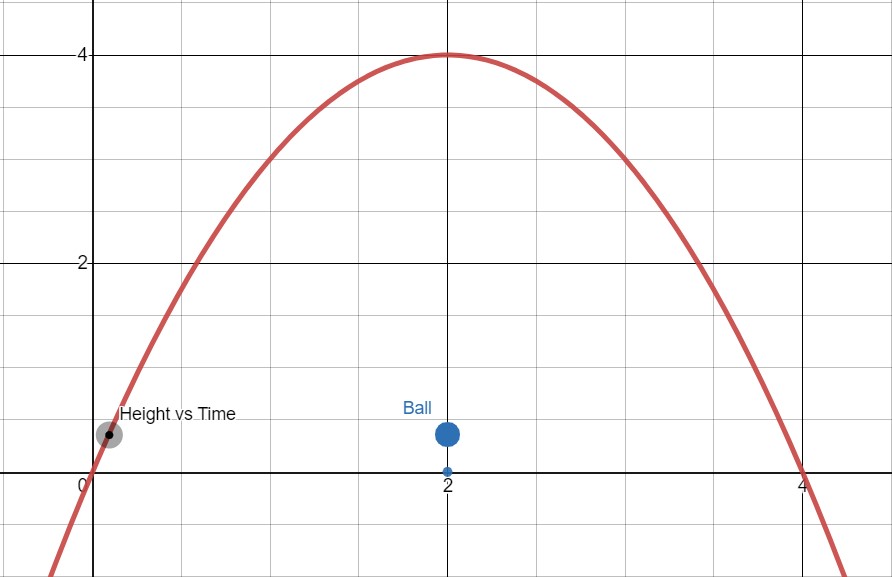
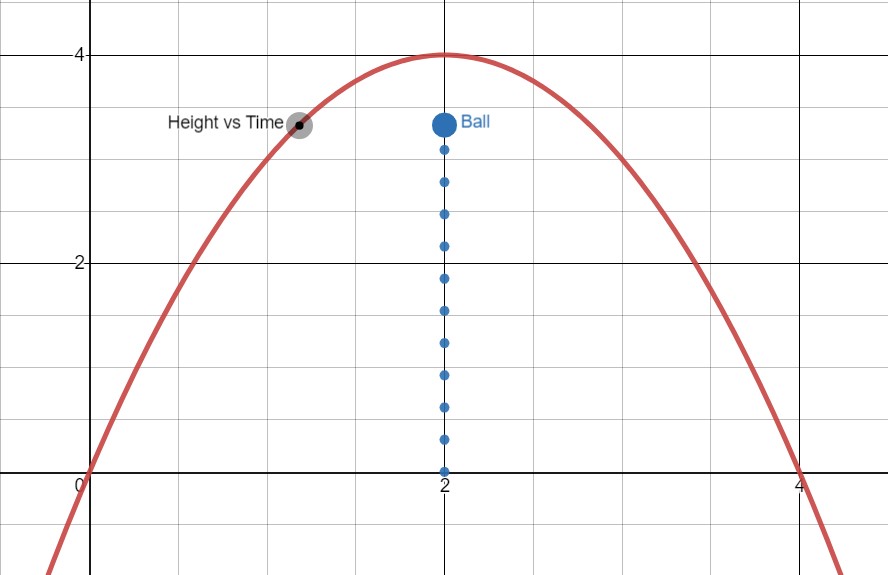
At the ball’s highest point, we have:
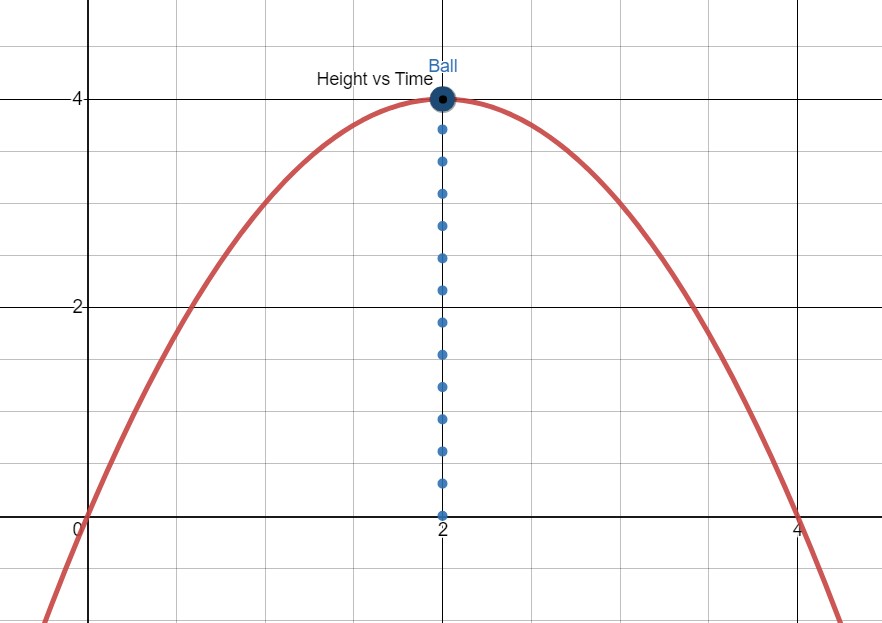
And as the ball goes down, we have:
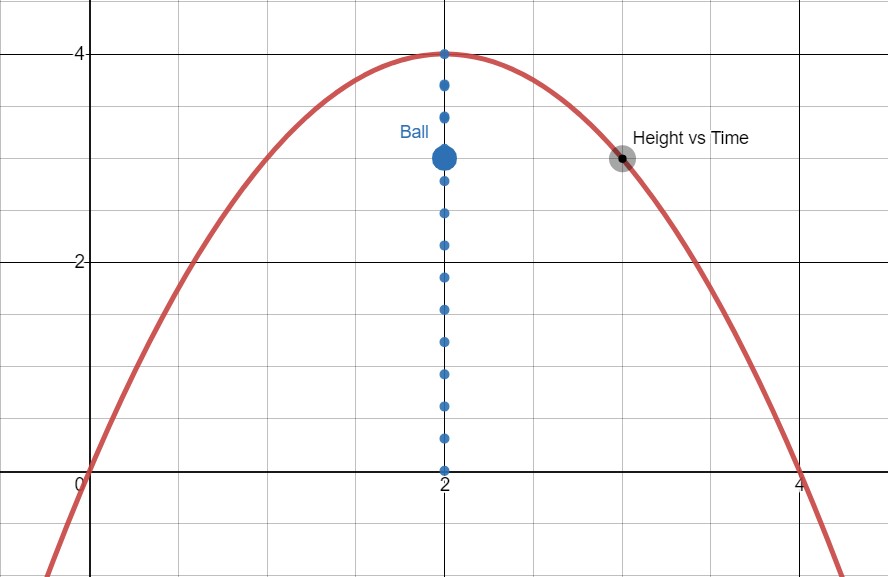
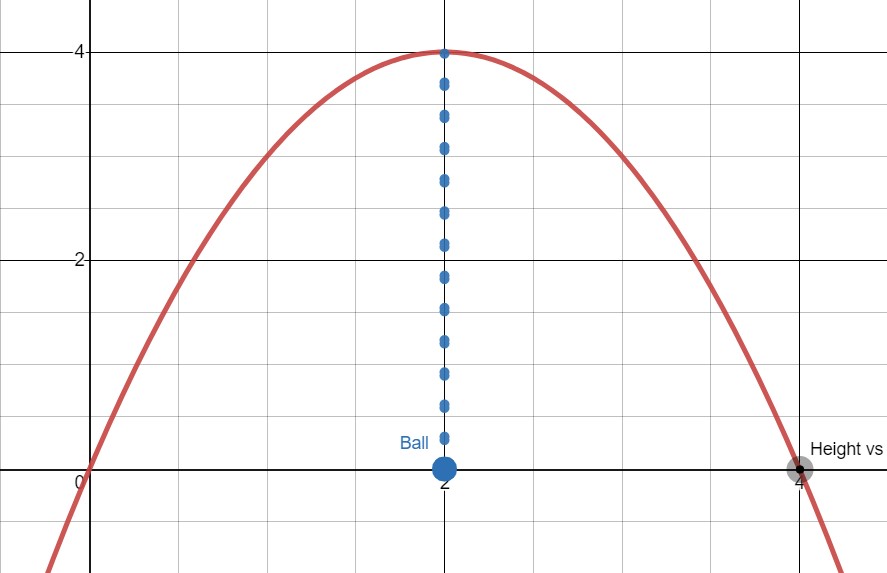
It is also important to note that in this situation, we know this model only makes sense from the time we throw the ball to the time it hits the ground. Having a negative distance would correspond with the ball going underground, which is not what we want to model. That means our domain will be from to the -value where the ball hits the ground.
This means, once again, we are back to wanting to know when the ball will hit the ground. Looking at the graph, we can focus on the time when the ball seems to hit the ground.
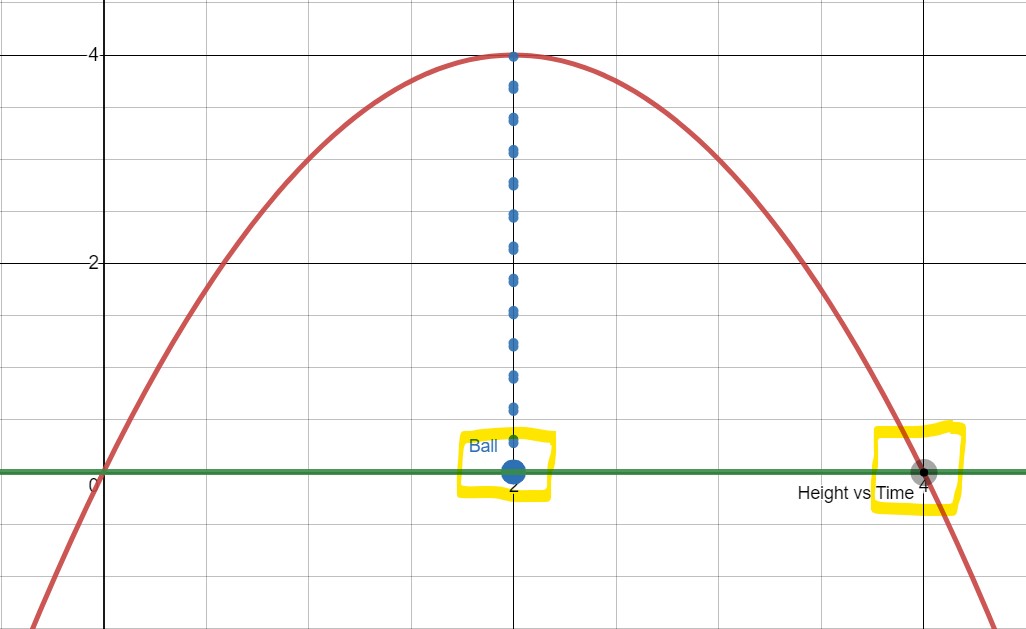
Notice that at the time the ball hits the ground, the function giving the distance vs. time graph, , is crossing the -axis. This means we are looking for the -value of the -intercept. That is, we are looking for when this function equals 0. We call an -value where a function equals zero the zero of a function. It can also be called the root of a function when the function is a polynomial. Occasionally, people will also call it the solution of a function but techincally they should say the solution of .
Let’s formalize this with a definition.
Finding Zeros Graphically
One method for finding zeros or roots of functions is to read them off the graph. Since the zero is the -coordinate of the -intercept, we are looking for the places where the graph crosses the -axis. This is where the -value or output will be zero. In the image below, the two roots are colored blue and green.
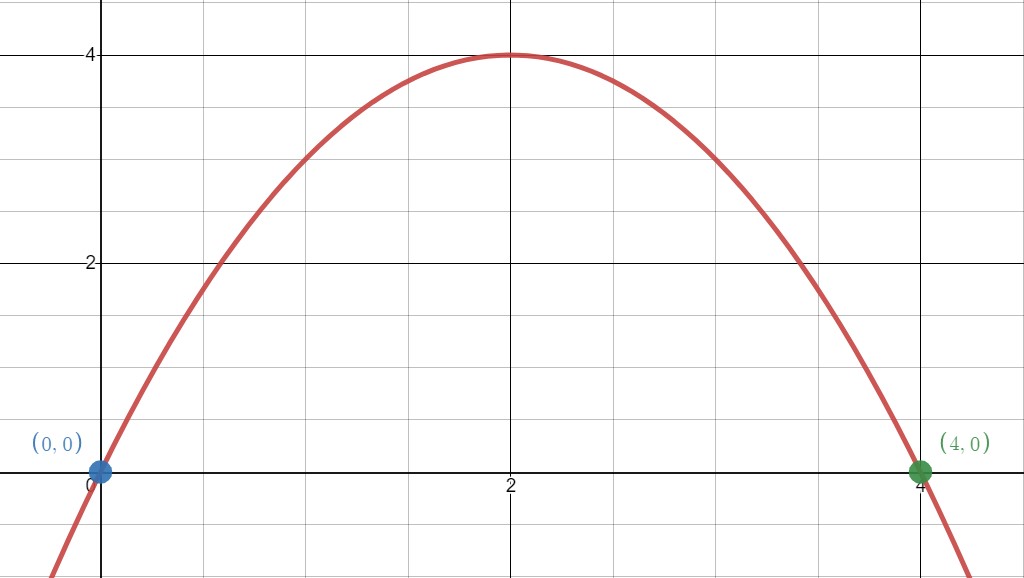
The root cooresponds to the blue dot at and represents when the ball is first thrown. The second root, labeled in green, is where . This root is the one we are looking for. The time when the ball hits the ground is 4 seconds after the ball is thrown.
Finding Zeros Algebraically
Reading zeros graphically can be useful, but it is not very precise. The root in our example could actually be at and we would not know from the graph. When possible, it is best to find zeros algebraically. To do this, we want to set and solve for . This algebra can get tricky. In this section, we will stick to relatively straightforward examples and in the next couple sections we will explore some more involved methods for solving equations where one side equals 0. It is not always possible to solve for the zeros of a function algebraically in this manner. In calculus, you will also learn methods to approximate zeros when it is not possible to solve for them exactly.
In our current example, we will have:
Recall that from the section on domains and ranges of composite functions.
Continuing, we have:
That is, the zeros or roots of are:
Considering our problem in context, we know that the root at time is when the ball was initially thrown, so the root at must be when the ball hits the ground.
Let’s look at a couple more examples:
This linear function only has one zero. This should make sense if we think about the graph of a line, as a line will only have one -intercept.
In fact, all linear functions except constant functions will have one zero. Constant functions will have no zeros except for the linear function in which every point is a zero.
To simplify this expression, notice that we need to know when . This is what we did in the last example. We know this happens at . Now, we also need to know when is positive and when it is negative.
Since we have the graph of the function above, we could look at it and see that when and when .
Alternatively, if we wanted to figure this out algebraically (without the graph), we can plug values into the function on either side of . This will work because we know a property about lines. We know that it cannot switch from positive to negative without being equal to 0 in the middle. You’ll learn about this later in the course.
Let’s choose to look at as a representative of values of and as a representive of values for .
This means that when .
This means that when .
Putting this all together, we can now write as a piecewise function:
Now we can find the zeros of this function. We know that an absolute value function is only zero where it switches from the positive branch to the negative branch of the piecewise function so the zero is when .
Let’s look at the graph of this function to verify that this makes sense.
By looking at this graph, we can see that the zero, that is the -intercept on is the same as on .
- We call an -value where a function equals zero the zero of a function. It can also be called the root of a function if the function is a polynomial. Another equivalent expression is the solution of . Another label for the same value is the -coordinate of the -intercept.
- You can find this value graphically by looking for the -value where the function crosses the -axis.
- You can find this value algebraically by setting and then solving for . This can sometimes be difficult (or even impossible!) to do.