- How to study, in a systematic way, ratios between the sides of a right triangle?
- What are the values of sine, cosine, and tangent, for the most frequent angles of , and ? And why?
Introduction
Recall that two triangles are called similar if one of them can be obtained by rescaling and moving around the other. Here’s an example:
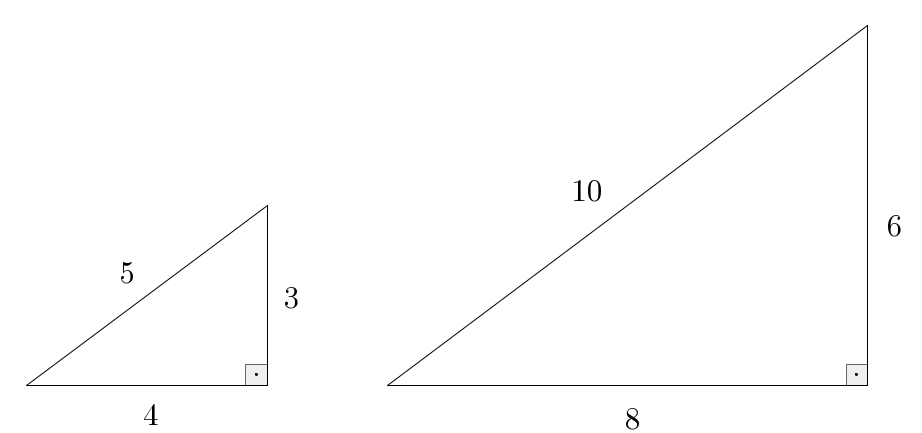
The dotted square symbol is a shorthand for “ degrees”. Triangles which have a angle are called right triangles, and will be the main focus of our discussion. What do similar triangles actually have in common? Certainly angles, but not necessarily the lengths of the sides. However, the ratios between any two sides of a triangle will remain the same, no matter how the triangle gets rescaled. Such ratios ultimately give us so much information about the given right triangle that they deserve special names: sine, cosine, and tangent.
Definitions and examples
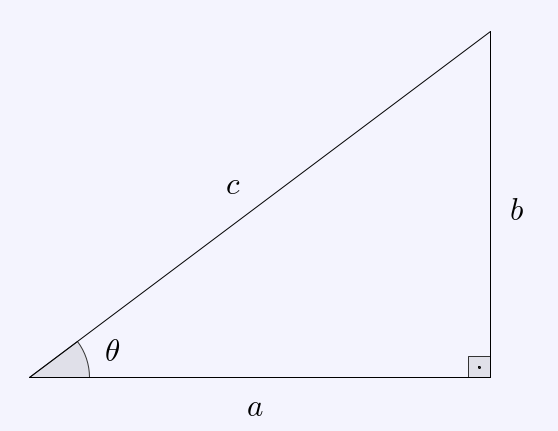
Then:
- The side labeled with is called the adjacent side to .
- The side labeled with is called the opposite side to .
- The side labeled with is called the hypotenuse of the triangle.
With this in place, we define the sine, cosine, and tangent of , by
- a.
- b.
- c.
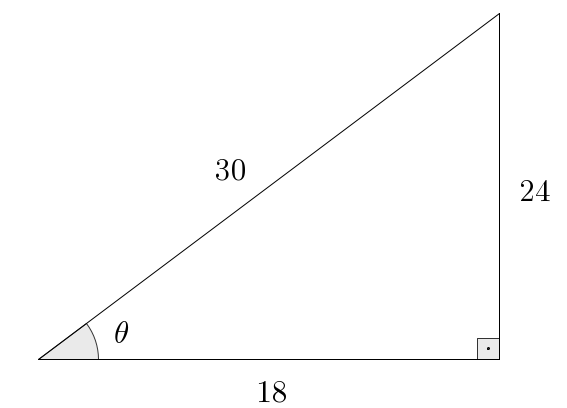
Often, one has information about the angles, but not about all the sides. Knowing , and helps us find out missing sides of a given right triangle. For that, the following fact is extremely important:
Why is this true? Consider again a right triangle like below:
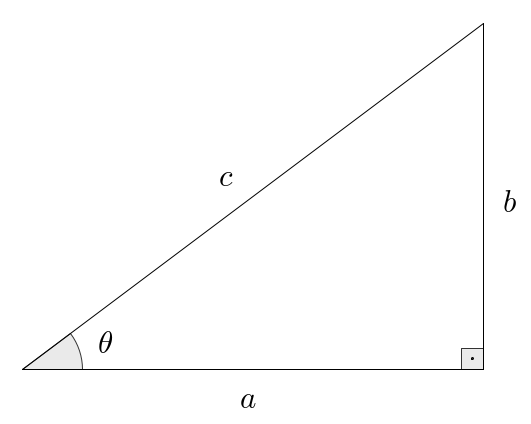
Then we know that and . But the Pythagorean theorem also says that . Putting all of this together, we have that as required.
Let’s see how to apply this.
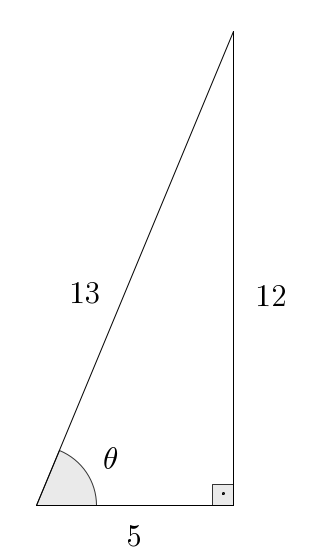
- a.
- Given: on
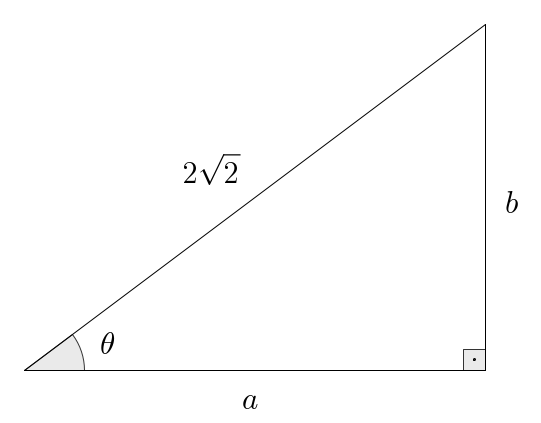
From the given information, we know that Now we use the Pythagorean theorem: the relation gives us that Alternatively, to find the value of , we can also use the fundamental identity to find first — which then yields . Here’s how this goes: and so . Thus as it should be. This is not something particular to this example: usually there is more than one strategy to solve this sort of problem. Which one is the best? You’ll be the judge. - b.
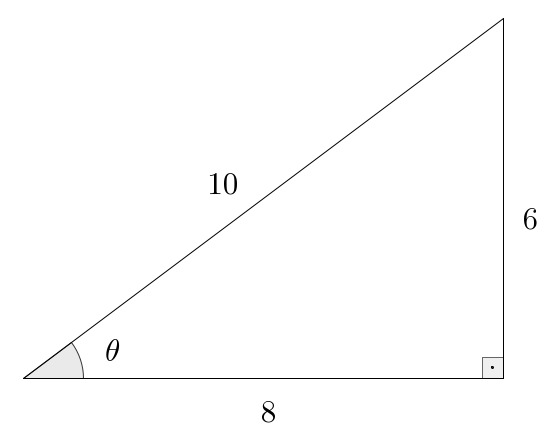
- Given: on
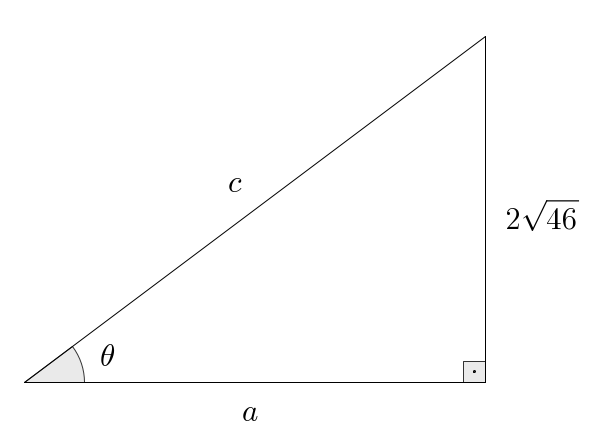
Since this time we were given , but also the opposite side to , which does not appear on the expression for , we must rely more on the Pythagorean theorem instead. In any case, we know that Now, the Pythagorean relation reads , and so: Continuing to manipulate this, we see that It remains to find the value of . So we go back to the beginning and compute
Values of trig functions for standard angles
We know that the sum of the inner angles of a triangle is always . For right triangles, one of the angles is , which means that the sum of the remaining two angles must also be . Frequently we encounter triangles whose angles are , and , and also triangles whose angles are , and .
These triangles have a special type of symmetry, which we’ll exploit to find the values of sine, cosine, and tangent, for , and . Finding the values of these trig functions for arbitrary angles by hand is a very difficult task. We will see later some trigonometric identities that may help us find such values for other angles but, in general, using a calculator (paying close attention to whether it is set to the right “units”) is the way to go.
For and
Consider an equilateral triangle of side length . Equilateral means that all the sides have the same length. This implies that all the inner angles must be equal and, since they must add up to , each of them equals . But also draw a height :
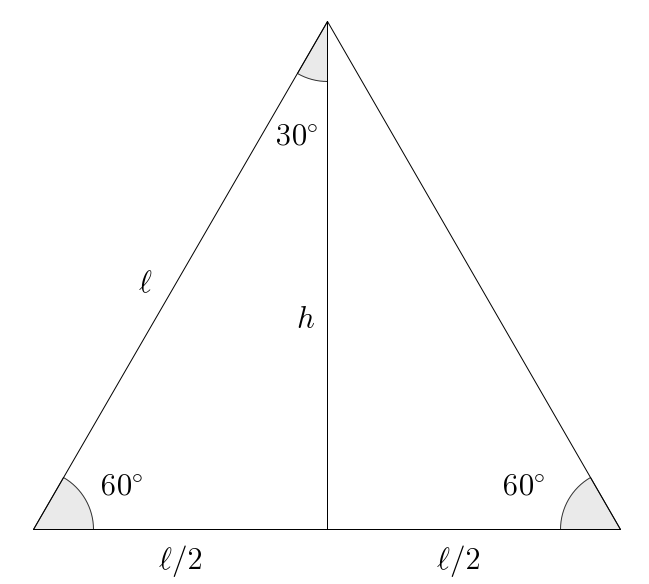
By the Pythagorean theorem, we know that and so we may compute:
Now, relative to the angle, we recognize
This means that as well as
To find the values of , , and , we can use the same triangle, noting that the opposite side to is the adjacent side to , and that the adjacent side to is the opposite side to . Since the hypotenuse is always the side opposite to the right angle, we conclude that and, finally, that
For
Consider a square of side length , and draw a diagonal .
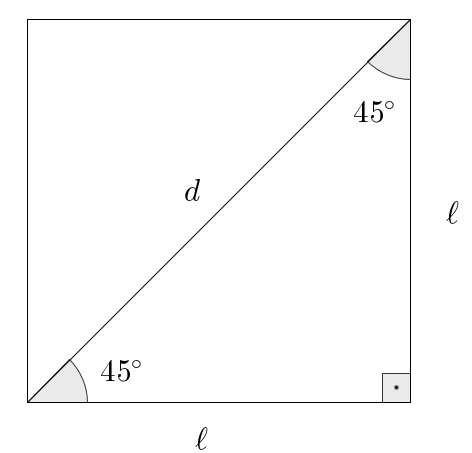
By the Pythagorean theorem, implies that . Relative to either of the angles, we have Hence
Standard values
We can summarize what we have discovered here in a table. Besides our standard angles of , , and , we can also consider and as extreme cases. Let’s do a quick thought experiment to understand this: if a right triangle had an angle of , this triangle would in fact collapse to a line segment, and we would have , while , suggesting we set and . Since and are complementary, we’re forced to set and . But while computing does not make sense, as we would have a division by . We say that is undefined, or that it does not exist (“DNE” for short, as usual). So, we have:
Those values should be committed to heart, but it’s easier than it seems. Here’s how you can think about it:
- No need to memorize the values for tangent: if you know and , you can just compute .
- No need to memorize the values for cosine: recall that the cosine of an angle is the sine of the complement. So if you know the values for sine, you’re in business.
- How to memorize the values for sine? The one thing you should remember here is that the values , , , and will appear. What is their order? Simple: write them in increasing order, just like the angles from to . So
- We have defined sine, cosine, and tangent, as ratios between sides of a right triangle. For each angle , the fundamental identity holds. It can be used together with the Pythagorean Theorem to get information about all sides of a given triangle, when some of them might be missing, provided you have some information about the angles.
- We have established the standard values of sine, cosine, and tangent, for the most frequent angles of , , and . Those values have been organized in a table. They are so frequent that knowing the values there by heart is useful, but exaggerated efforts into memorizing the table should not be wasted — understanding how the values are deduced pays off more in the long run.