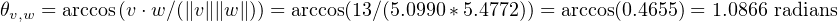Consider equipped with its standard basis (so that vectors in are canonically identified with their coordinate representations). Then given , their dot product (also referred to as scalar product) is given by
This operation on pairs of vectors satisfies three basic properties
- (IP1)
- It is symmetric:
- (IP2)
- It is bilinear:
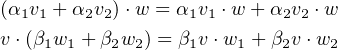
- (IP3)
- It is positive non-degenerate:
Note that the standard Euclidean norm of (also referred to as the -norm) is closely related to the dot product; precisely
Its essential features are
- (N1)
- It is positive definite:
- (N2)
- It satisfies the triangle inequality (for norms):
This is the norm used in to define the standard Euclidean metric, which is the conventional way to measure the distance between two vectors:
Again, this distance function - or metric - satisfies three basic properties, which are direct consequences of the ones above.
- (M1)
- It is symmetric:
- (M2)
- It is positive non-degenerate:
- (M3
- ) It satisfies the triangle inequality (for metrics):
So the i) dot product, ii) Euclidean norm, and iii) Euclidean distance are all closely related. In fact, any one of them determines the other two. Obviously, the dot product determines the norm, and the norm determines the distance. But also one has
- the equality so that one can also recover the dot product from the norm;
- , so and determine each other.
If , are two non-zero vectors in , then there span is at most two-dimensional, and so we may choose a plane in containing them. Within that plane the vectors determine two angles. We define to be the smaller of the two angles; this angle will always lie between and radians
[Note: Except in the case the two vectors are colinear and pointing in opposite directions, the smaller angle will be unique and less than radians. In that one remaining case the choice of angle representative will not be unique, but both angles will be equal to , so the angle itself is well-defined.]
The angle formula is given by the following lemma.
As is 1-1 on the interval , this equality implies