The dot product defined in the previous section is a specific example of a bilinear, symmetric, positive definite pairing on the vector space . We consider these properties in sequence, for an arbitrary vector space over .
A bilinear pairing on is a map which simply satisfies property
(IP2)
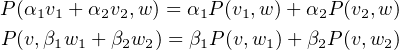
A symmetric bilinear pairing is a bilinear pairing that also satisfies
(IP1)
These pairings admit a straightforward matrix representation, not unlike the matrix representation of linear transformations discussed previously. Again, we assume we are looking at coordinate vectors with respect to the standard basis for .
- Proof
- Because it is bilinear, is uniquely characterized by its values on ordered pairs of basis vectors; moreover two bilinear pairings are equal precisely if for all pairs . So define be the matrix with entry given by By construction, the pairing is bilinear, and agrees with on ordered pairs of basis vectors. Thus the two agree everywhere. This establishes a 1-1 correspondence (bilinear pairings on ) ( matrices). Again, by construction, the matrix will be symmetric iff is. Thus this correspondence restricts to a 1-1 correspondence (symmetric bilinear pairings on ) ( symmetric matrices).
(IP3)
However, unlike properties (IP1) and (IP2), (IP3) is harder to translate into properties of the representing matrix. In fact, this last property is closely related to the property of diagonalizability for symmetric matrices.
- Proof
- As is symmetric, it is diagonalizable; hence has a basis where each
is an eigenvector of .
Suppose is positive definite. Then for each one has and as for each the last inequality implies for each .
On the other hand, suppose all of the eigenvalues are positive. Let be an arbitrary non-zero vector in . As is a basis can be written uniquely as a linear combination of the vectors in : where at least one of the coefficients . Then
To see why this is, consider the sequence of equalities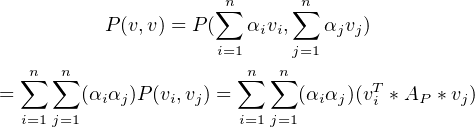
(0.1)
(0.2)In other words, . But since this must mean that .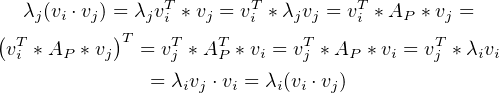
Now if is a repeated eigenvalue, this argument doesn’t work. The trick is to choose the basis with a bit of care. Let be an eigenvalue of , with corresponding eigenspace . We will see below that the subspace has an orthogonal basis ; one where whenever . So for each eigenvalue choose an orthogonal basis . Then let be the union of all of the orthogonal basis sets . Because is diagonalizable, , the direct sum of the eigenspaces of . Since , as just defined, is a basis for , it is a basis for .
By the previous claim, this is true if the two basis vectors lie in different eigenspaces. But if for some eigenvalue then by the orthogonality of the basis for , proving the claim.Returning to the sum in eq. (0.2) above, using this basis , we have Since for each and , this sum must always be non-negative. Moreover, the only way it can be zero is if each term is zero, which can only happen if for each . In other words, is positive definite, completing the proof.
For this reason we call a real symmetric matrix positive definite iff all of its eigenvalues are positive.
It is conventional in mathematics to denote inner products, and more generally bilinear pairings, by the symbol . In other words, a bilinear pairing on a vector space is denoted by
We have seen how a given bilinear pairing on is represented by an matrix, and conversely, how any matrix can be used to define a bilinear pairing on . The same is true more generally for bilinear pairings on an -dimensional vector space . The proof of the following theorem follows exactly as in the case for equipped with the standard basis (the case we looked at above).