The properties for this pairing differ slightly than the corresponding ones for the real case, for reasons that will become clear shortly. They are

(HIP1)
It is conjugate-symmetric:
(HIP2)
It is linear in the first variable and conjugate linear in the second:
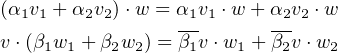
(α1v1 + α2v2)⋅w = α1v1 ⋅w + α2v2 ⋅w v ⋅(β w + β w ) = β-v ⋅w + β-v⋅w 1 1 2 2 1 1 2 2
(HIP3)
It is positive non-degenerate:

An inner product on a complex vector space satisfying these three properties is usually referred to as a Hermitian inner product, the one just defined for being the standard Hermitian inner product, or complex scalar product.

As in the real case, the norm of (also referred to as the -norm) is closely related to the complex scalar product; precisely

This norm on complex -space satisfies the same two properties as before:

(N1)
It is positive definite:
(N2)
It satisfies the triangle inequality (for norms):

This norm on defines the standard metric, which is the standard way to measure the distance between two vectors in complex -space:

This distance function - or metric - satisfies the same three basic properties as it does in the real case:

(M1)
It is symmetric:
(M2)
It is positive non-degenerate:
(M3
) It satisfies the triangle inequality (for metrics):

So the i) complex scalar product, ii) standard complex norm, and iii) complex distance are all related; moreover as in the real case the norm and distance functions determine one another. However, in the complex case it is no longer true that one can recover the inner product from the norm. It is only the real part that can be expressed this way: